Fundamentals of Heat and Mass Transfer
7th Edition
ISBN: 9780470501979
Author: Frank P. Incropera, David P. DeWitt, Theodore L. Bergman, Adrienne S. Lavine
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 2, Problem 2.38P
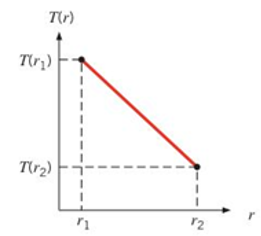
One-dimensional, steady-state conduction with no energy generation is occurring in a cylindrical shell of inner radius
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Continuity equation
A
y
x
dx
D
T
معادلة الاستمرارية
Ly
X
Q/Prove that
ди
хе
+ ♥+ ㅇ?
he
me
ze
ོ༞“༠ ?
Q
Derive (continuity equation)?
I want to derive clear mathematics.
motor supplies 200 kW at 6 Hz to flange A of the shaft shown in Figure. Gear B transfers 125 W of power to operating machinery in the factory, and the remaining power in the shaft is mansferred by gear D. Shafts (1) and (2) are solid aluminum (G = 28 GPa) shafts that have the same diameter and an allowable shear stress of t= 40 MPa. Shaft (3) is a solid steel (G = 80 GPa) shaft with an allowable shear stress of t = 55 MPa. Determine:
a) the minimum permissible diameter for aluminum shafts (1) and (2)
b) the minimum permissible diameter for steel shaft (3).
c) the rotation angle of gear D with respect to flange A if the shafts have the minimum permissible diameters as determined in (a) and (b).
Chapter 2 Solutions
Fundamentals of Heat and Mass Transfer
Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - Assume steady-state, one-dimensional conduction in...Ch. 2 - A hot water pipe with outside radius r, has a...Ch. 2 - A spherical shell with inner radius r1 and outer...Ch. 2 - Assume steady-state, one-dimensional heat...Ch. 2 - A composite rod consists of two different...Ch. 2 - A solid, truncated cone serves as a support for a...Ch. 2 - To determine the effect of the temperature...Ch. 2 - A young engineer is asked to design a thermal...Ch. 2 - A one-dimensional plane wall of thickness 2L=100mm...
Ch. 2 - Consider steady-state conditions for...Ch. 2 - Consider a plane wall 100 mm thick and of thermal...Ch. 2 - A cylinder of radius ro, length L, and thermal...Ch. 2 - In the two-dimensional body illustrated, the...Ch. 2 - Consider the geometry of Problem 2.14 for the case...Ch. 2 - Steady-state, one-dimensional conduction occurs in...Ch. 2 - An apparatus for measuring thermal conductivity...Ch. 2 - An engineer desires to measure the thermal...Ch. 2 - Consider a 300mm300mm window in an aircraft. For a...Ch. 2 - Consider a small but known volume of metal that...Ch. 2 - Use INT to perform the following tasks. Graph the...Ch. 2 - Calculate the thermal conductivity of air,...Ch. 2 - A method for determining the thermal conductivity...Ch. 2 - Compare and contrast the heat capacity cp of...Ch. 2 - A cylindrical rod of stainless steel is insulated...Ch. 2 - At a given instant of time, the temperature...Ch. 2 - A pan is used to boil water by placing it on a...Ch. 2 - Uniform internal heat generation at q=5107W/m3 is...Ch. 2 - Consider a one-dimensional plane wall with...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - The temperature distribution across a wall 0.3 m...Ch. 2 - Prob. 2.33PCh. 2 - One-dimensional, steady-state conduction with...Ch. 2 - Derive the heat diffusion equation, Equation 2.26,...Ch. 2 - Derive the heat diffusion equation, Equation 2.29....Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - One-dimensional, steady-state conduction with no...Ch. 2 - The steady-state temperature distribution in a...Ch. 2 - Prob. 2.41PCh. 2 - Prob. 2.42PCh. 2 - cylindrical system illustrated has negligible...Ch. 2 - Beginning with a differential control volume in...Ch. 2 - Prob. 2.45PCh. 2 - Prob. 2.46PCh. 2 - For a long circular tube of inner and outer radii...Ch. 2 - Passage of an electric current through a long...Ch. 2 - Two-dimensional. steady-state conduction occurs in...Ch. 2 - An electric cable of radius r1 and thermal...Ch. 2 - A spherical shell of inner and outer radii ri and...Ch. 2 - A chemically reacting mixture is stored in a...Ch. 2 - A thin electrical heater dissipating 4000W/m2 is...Ch. 2 - The one-dimensional system of mass M with constant...Ch. 2 - Consider a one-dimensional plane wall of thickness...Ch. 2 - A large plate of thickness 2L is at a uniform...Ch. 2 - The plane wall with constant properties and no...Ch. 2 - Consider the steady-state temperature...Ch. 2 - A plane wall has constant properties, no internal...Ch. 2 - A plane wall with constant properties is initially...Ch. 2 - Consider the conditions associated with Problem...Ch. 2 - Consider the steady-state temperature distribution...Ch. 2 - A spherical particle of radius r1 experiences...Ch. 2 - Prob. 2.64PCh. 2 - A plane wall of thickness L=0.1m experiences...Ch. 2 - Prob. 2.66PCh. 2 - A composite one-dimensional plane wall is of...Ch. 2 - Typically, air is heated in a hair dryer by...Ch. 2 - Prob. 2.69P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- First monthly exam Gas dynamics Third stage Q1/Water at 15° C flow through a 300 mm diameter riveted steel pipe, E-3 mm with a head loss of 6 m in 300 m length. Determine the flow rate in pipe. Use moody chart. Q2/ Assume a car's exhaust system can be approximated as 14 ft long and 0.125 ft-diameter cast-iron pipe ( = 0.00085 ft) with the equivalent of (6) regular 90° flanged elbows (KL = 0.3) and a muffler. The muffler acts as a resistor with a loss coefficient of KL= 8.5. Determine the pressure at the beginning of the exhaust system (pl) if the flowrate is 0.10 cfs, and the exhaust has the same properties as air.(p = 1.74 × 10-3 slug/ft³, u= 4.7 x 10-7 lb.s/ft²) Use moody chart (1) MIDAS Kel=0.3 Q3/Liquid ammonia at -20°C is flowing through a 30 m long section of a 5 mm diameter copper tube(e = 1.5 × 10-6 m) at a rate of 0.15 kg/s. Determine the pressure drop and the head losses. .μ= 2.36 × 10-4 kg/m.s)p = 665.1 kg/m³arrow_forward2/Y Y+1 2Cp Q1/ Show that Cda Az x P1 mactual Cdf Af R/T₁ 2pf(P1-P2-zxgxpf) Q2/ A simple jet carburetor has to supply 5 Kg of air per minute. The air is at a pressure of 1.013 bar and a temperature of 27 °C. Calculate the throat diameter of the choke for air flow velocity of 90 m/sec. Take velocity coefficient to be 0.8. Assume isentropic flow and the flow to be compressible. Quiz/ Determine the air-fuel ratio supplied at 5000 m altitude by a carburetor which is adjusted to give an air-fuel ratio of 14:1 at sea level where air temperature is 27 °C and pressure is 1.013 bar. The temperature of air decreases with altitude as given by the expression The air pressure decreases with altitude as per relation h = 19200 log10 (1.013), where P is in bar. State any assumptions made. t = ts P 0.0065harrow_forward36 2) Use the method of MEMBERS to determine the true magnitude and direction of the forces in members1 and 2 of the frame shown below in Fig 3.2. 300lbs/ft member-1 member-2 30° Fig 3.2. https://brightspace.cuny.edu/d21/le/content/433117/viewContent/29873977/Viewarrow_forward
- Can you solve this for me?arrow_forward5670 mm The apartment in the ground floor of three floors building in Fig. in Baghdad city. The details of walls, roof, windows and door are shown. The window is a double glazing and air space thickness is 1.3cm Poorly Fitted-with Storm Sash with wood strip and storm window of 0.6 cm glass thickness. The thickness of door is 2.5 cm. The door is Poor Installation. There are two peoples in each room. The height of room is 280 cm. assume the indoor design conditions are 25°C DBT and 50 RH, and moisture content of 8 gw/kga. The moisture content of outdoor is 10.5 gw/kga. Calculate heat gain for living room : الشقة في الطابق الأرضي من مبنى ثلاثة طوابق في مدينة بغداد يظهر في مخطط الشقة تفاصيل الجدران والسقف والنوافذ والباب. النافذة عبارة عن زجاج مزدوج وسمك الفراغ الهوائي 1.3 سم ضعيف الاحكام مع ساتر حماية مع إطار خشبي والنافذة بسماكة زجاج 0.6 سم سماكة الباب 2.5 سم. الباب هو تركيب ضعيف هناك شخصان في كل غرفة. ارتفاع الغرفة 280 سم. افترض أن ظروف التصميم الداخلي هي DBT25 و R50 ، ومحتوى الرطوبة 8…arrow_forwardHow do i solve this problem?arrow_forward
- Q4/ A compressor is driven motor by mean of a flat belt of thickness 10 mm and a width of 250 mm. The motor pulley is 300 mm diameter and run at 900 rpm and the compressor pulley is 1500 mm diameter. The shaft center distance is 1.5 m. The angle of contact of the smaller pulley is 220° and on the larger pulley is 270°. The coefficient of friction between the belt and the small pulley is 0.3, and between the belt and the large pulley is 0.25. The maximum allowable belt stress is 2 MPa and the belt density is 970 kg/m³. (a) What is the power capacity of the drive and (b) If the small pulley replaced by V-grooved pulley of diameter 300 mm, grooved angle of 34° and the coefficient of friction between belt and grooved pulley is 0.35. What will be the power capacity in this case, assuming that the diameter of the large pulley remain the same of 1500 mm.arrow_forwardYou are tasked with designing a power drive system to transmit power between a motor and a conveyor belt in a manufacturing facility as illustrated in figure. The design must ensure efficient power transmission, reliability, and safety. Given the following specifications and constraints, design drive system for this application: Specifications: Motor Power: The electric motor provides 10 kW of power at 1,500 RPM. Output Speed: The output shaft should rotate at 150 rpm. Design Decisions: Transmission ratio: Determine the necessary drive ratio for the system. Shaft Diameter: Design the shafts for both the motor and the conveyor end. Material Selection: Choose appropriate materials for the gears, shafts. Bearings: Select suitable rolling element bearings. Constraints: Space Limitation: The available space for the gear drive system is limited to a 1-meter-long section. Attribute 4 of CEP Depth of knowledge required Fundamentals-based, first principles analytical approach…arrow_forward- | العنوان In non-continuous dieless drawing process for copper tube as shown in Fig. (1), take the following data: Do-20mm, to=3mm, D=12mm, ti/to=0.6 and v.-15mm/s. Calculate: (1) area reduction RA, (2) drawing velocity v. Knowing that: ti: final thickness V. Fig. (1) ofthrearrow_forward
- A direct extrusion operation produces the cross section shown in Fig. (2) from an aluminum billet whose diameter 160 mm and length - 700 mm. Determine the length of the extruded section at the end of the operation if the die angle -14° 60 X Fig. (2) Note: all dimensions in mm.arrow_forwardFor hot rolling processes, show that the average strain rate can be given as: = (1+5)√RdIn(+1)arrow_forward: +0 usão العنوان on to A vertical true centrifugal casting process is used to produce bushings that are 250 mm long and 200 mm in outside diameter. If the rotational speed during solidification is 500 rev/min, determine the inside radii at the top and bottom of the bushing if R-2R. Take: -9.81 mis ۲/۱ ostrararrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Principles of Heat Transfer (Activate Learning wi...Mechanical EngineeringISBN:9781305387102Author:Kreith, Frank; Manglik, Raj M.Publisher:Cengage Learning
Principles of Heat Transfer (Activate Learning wi...
Mechanical Engineering
ISBN:9781305387102
Author:Kreith, Frank; Manglik, Raj M.
Publisher:Cengage Learning
Understanding Conduction and the Heat Equation; Author: The Efficient Engineer;https://www.youtube.com/watch?v=6jQsLAqrZGQ;License: Standard youtube license