
Concept explainers
(a)
Find the amplitude of the motion
(a)
Answer to Problem 19.110P
The amplitude of the motion
Explanation of Solution
Given information:
The weight of the bob
The weight of the collar
The length of the simple pendulum (l) is
The amplitude of the collar
The magnitude of static deflection
The frequency
The acceleration due to gravity (g) is
Calculation:
Calculate the mass of the bob
Substitute
Calculate the mass of the collar
Substitute
Calculate the frequency of the period
Substitute
Show the system at before and after moving the collar horizontally as in Figure 1.
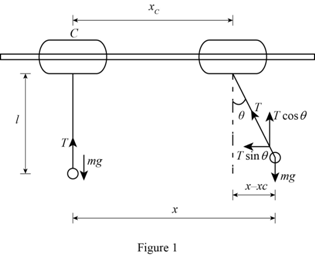
Refer Figure (1),
Before giving horizontal movement, the force mg is equal to the tension in the pendulum.
The expression for the force balance equation for initial condition as follows:
Calculate the value of
The expression for the force balance equation in x-direction in the displaced condition as follows:
Here,
The only force in the x-direction is the tension component
Substitute
Calculate the differential equation of motion using the formula:
Substitute mg for T and
Substitute
Here,
Compare the differential equation (2) with the general differential equation of motion for forced vibration
Calculate the natural circular frequency of vibration
Substitute
Calculate the amplitude of the forced vibration
Substitute
Therefore, the amplitude of the motion
(b)
Find the force that must be applied to collar C (F) to maintain the motion.
(b)
Answer to Problem 19.110P
The force that must be applied to collar C (F) to maintain the motion is
Explanation of Solution
Given information:
The weight of the bob
The weight of the collar
The length of the simple pendulum (l) is
The amplitude of the collar
The magnitude of static deflection
The frequency
The acceleration due to gravity (g) is
Calculation:
Consider the collar as a free body and show the free body diagram equation as in Figure (2).
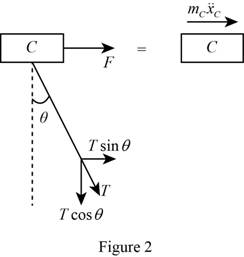
Refer Figure (2), F is the force applied to the collar to maintain the motion is F and
The expression for the force balance equation from Figure 2 as follows:
Substitute mg for T and
Substitute
The expression for the relation for
Differentiate the relation for
Substitute
Substitute
Therefore, the force that must be applied to collar C (F) to maintain the motion is
Want to see more full solutions like this?
Chapter 19 Solutions
VECTOR MECH...,STAT.+DYN.(LL)-W/ACCESS
- 5. A flow is field given by V = x²₁³+xy, and determine 3 ·y³j- (a) Whether this is a one, two- or three-dimensional flow (b) Whether it is a possible incompressible flow (c) Determine the acceleration of a fluid particle at the location (X,Y,Z)=(1,2,3) (d) Whether the flow is rotational or irrotational flow?arrow_forwardSolve this problem and show all of the workarrow_forwardSolve this problem and show all of the workarrow_forward
- draw the pneumatic circuit to operate a double-acting cylinder with: 1. Extension: Any of two manual conditions plus cylinder fully retracted, → Extension has both meter-in and meter-out, 2. Retraction: one manual conditions plus cylinder fully extended, → Retraction is very fast using quick exhaust valve.arrow_forwardCorrect answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you. Expert solution plsarrow_forwardCorrect answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you.arrow_forward
- Correct answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution only with fbd. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution only. I will upvote, thank you.arrow_forward
- Correct answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution only. I will upvote, thank you.arrow_forwardCorrect answer is written below. Detailed and complete solution with fbd only. I will upvote, thank you.arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





