Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e
5th Edition
ISBN: 9781323132098
Author: Thomas, Lay
Publisher: PEARSON C
bartleby

Videos

Textbook Question
Book Icon
Chapter 1.9, Problem 28E

In Exercises 25-28, determine if the specified linear transformation is (a) one-to-one and (b) onto. Justify each answer.

28. The transformation in Exercise 14

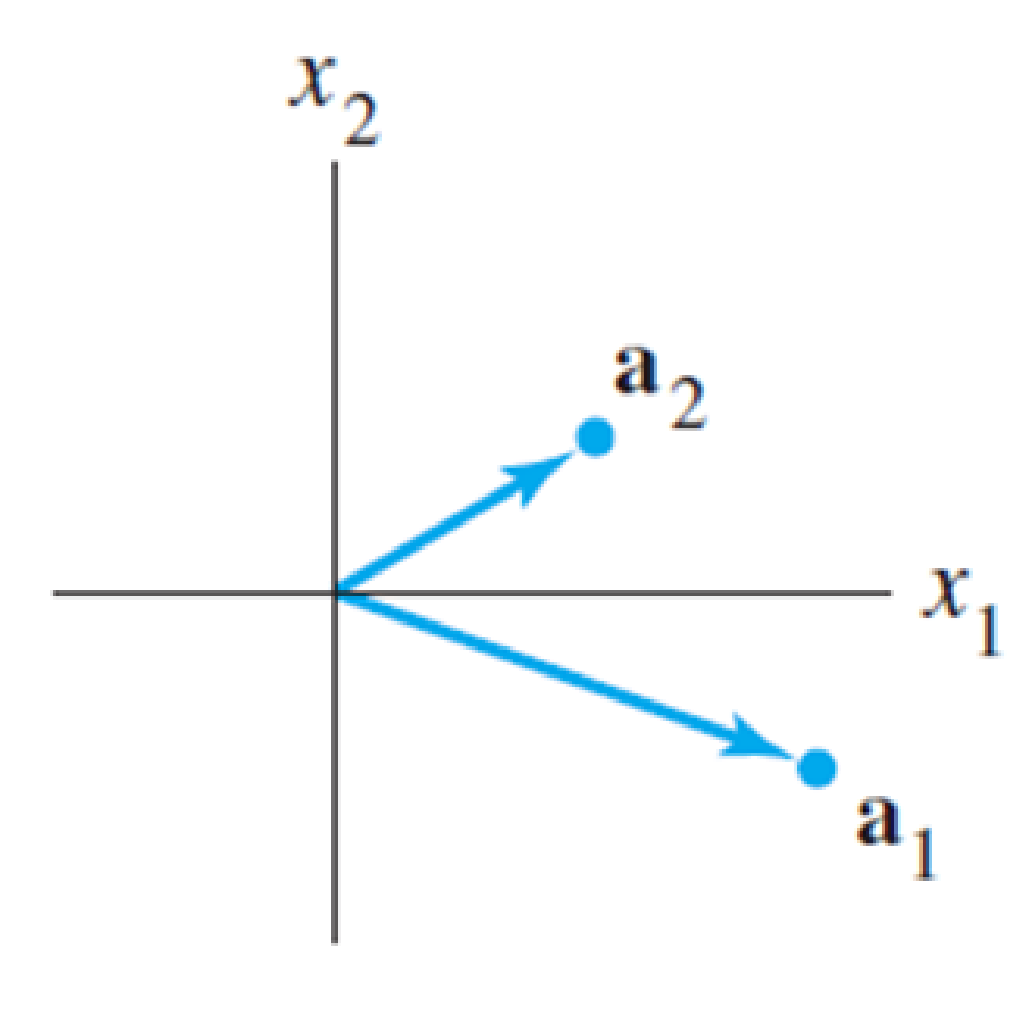
14. Let T : ℝ2 → ℝ2 be a linear transformation with standard matrix A = [a1 a2], where a1 and a2 are shown in the figure. Using the figure, draw the image of [ − 1 3 ] under the transformation T.

Chapter 1.9, Problem 28E, In Exercises 25-28, determine if the specified linear transformation is (a) one-to-one and (b) onto.

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 1.9, Problem 27E
Next
Chapter 1.9, Problem 29E
Students have asked these similar questions
Which rule describes the transformation b
Determine whether the function L: P2 → P2 defined by L(a0 +a1x+a2x2) = a1 +2a2xis a linear transformation. Explain, and show all your work.
I really need help with

Chapter 1 Solutions

Thomas' Calculus and Linear Algebra and Its Applications Package for the Georgia Institute of Technology, 1/e

Ch. 1.1 - State in words the next elementary row operation...Ch. 1.1 - The augmented matrix of a linear system has been...Ch. 1.1 - Is (3, 4, 2) a solution of the following system?...Ch. 1.1 - For what values of h and k is the following system...Ch. 1.1 - Solve each system in Exercises 1-4 by using...Ch. 1.1 - Solve each system in Exercises 1-4 by using...Ch. 1.1 - Find the point (x1, x2) that lies on the line x1 +...Ch. 1.1 - Find the point of intersection of the lines x1 ...Ch. 1.1 - Consider each matrix in Exercises 5 and 6 as the...Ch. 1.1 - Consider each matrix in Exercises 5 and 6 as the...
Ch. 1.1 - In Exercises 7-10, the augmented matrix of a...Ch. 1.1 - In Exercises 7-10, the augmented matrix of a...Ch. 1.1 - In Exercises 7-10, the augmented matrix of a...Ch. 1.1 - In Exercises 7-10, the augmented matrix of a...Ch. 1.1 - Solve the systems in Exercises 11-14. 11....Ch. 1.1 - Solve the systems in Exercises 11-14. 12....Ch. 1.1 - Solve the systems in Exercises 11-14. 13....Ch. 1.1 - Solve the systems in Exercises 11-14....Ch. 1.1 - Determine if the systems in Exercises 15 and 16...Ch. 1.1 - Determine if the systems in Exercises 15 and 16...Ch. 1.1 - Do the three lines x1 4x2 = 1, 2x1 x2 = 3, and...Ch. 1.1 - Do the three planes x1 + 2x2 + x3 = 4, x2 x3 = 1,...Ch. 1.1 - In Exercises 19-22, determine the value(s) of h...Ch. 1.1 - In Exercises 19-22, determine the value(s) of h...Ch. 1.1 - In Exercises 19-22, determine the value(s) of h...Ch. 1.1 - In Exercises 19-22, determine the value(s) of h...Ch. 1.1 - In Exercises 23 and 24, key statements from this...Ch. 1.1 - In Exercises 23 and 24, key statements from this...Ch. 1.1 - Find an equation involving g, h, and k that makes...Ch. 1.1 - Construct three different augmented matrices for...Ch. 1.1 - Suppose the system below is consistent for all...Ch. 1.1 - Suppose a, b, c, and d are constants such that a...Ch. 1.1 - In Exercises 29-32, find the elementary row...Ch. 1.1 - In Exercises 29-32, find the elementary row...Ch. 1.1 - In Exercises 29-32, find the elementary row...Ch. 1.1 - In Exercises 29-32, find the elementary row...Ch. 1.1 - An important concern in the study of heat transfer...Ch. 1.1 - Solve the system of equations from Exercise 33....Ch. 1.2 - Find the general solution of the linear system...Ch. 1.2 - Find the general solution of the system...Ch. 1.2 - Suppose a 4 7 coefficient matrix for a system of...Ch. 1.2 - In Exercises 1 and 2, determine which matrices arc...Ch. 1.2 - In Exercises 1 and 2, determine which matrices are...Ch. 1.2 - Row reduce the matrices in Exercises 3 and 4 to...Ch. 1.2 - Row reduce the matrices in Exercises 3 and 4 to...Ch. 1.2 - Describe the possible echelon forms of a nonzero 2...Ch. 1.2 - Repeat Exercise 5 for a nonzero 3 2 matrix. 5....Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Find the general solutions of the systems whose...Ch. 1.2 - Exercises 15 and 16 use the notation of Example 1...Ch. 1.2 - Exercises 15 and 16 use the notation of Example 1...Ch. 1.2 - In Exercises 17 and 18, determine the value(s) of...Ch. 1.2 - In Exercises 17 and 18, determine the value(s) of...Ch. 1.2 - In Exercises 19 and 20, choose h and k such that...Ch. 1.2 - In Exercises 19 and 20, choose h and k such that...Ch. 1.2 - In Exercises 21 and 22, mark each statement True...Ch. 1.2 - In Exercises 21 and 22, mark each statement True...Ch. 1.2 - Suppose a 3 5 coefficient matrix for a system has...Ch. 1.2 - Suppose a system of linear equations has a 3 5...Ch. 1.2 - Suppose the coefficient matrix of a system of...Ch. 1.2 - Suppose the coefficient matrix of a linear system...Ch. 1.2 - Restate the last sentence in Theorem 2 using the...Ch. 1.2 - What would you have to know about the pivot...Ch. 1.2 - A system of linear equations with fewer equations...Ch. 1.2 - Give an example of an inconsistent underdetermined...Ch. 1.2 - A system of linear equations with more equations...Ch. 1.2 - Suppose an n (n + 1) matrix is row reduced to...Ch. 1.2 - Find the interpolating polynomial p(t) = a0 + a1t...Ch. 1.2 - [M] In a wind tunnel experiment, die force on a...Ch. 1.3 - Prob. 1PPCh. 1.3 - For what value(s) of h will y be in Span{v1, v2,...Ch. 1.3 - Let w1, w2, w3, u, and v be vectors in n. Suppose...Ch. 1.3 - In Exercises 1 and 2, compute u + v and u 2v. 1....Ch. 1.3 - In Exercises 1 and 2, compute u + v and u 2v. 2....Ch. 1.3 - In Exercises 3 and 4, display the following...Ch. 1.3 - In Exercises 3 and 4, display the following...Ch. 1.3 - In Exercises 5 and 6, write a system of equations...Ch. 1.3 - In Exercises 5 and 6, write a system of equations...Ch. 1.3 - Use the accompanying figure to write each vector...Ch. 1.3 - Use the accompanying figure to write each vector...Ch. 1.3 - In Exercises 9 and 10, write a vector equation...Ch. 1.3 - In Exercises 9 and 10, write a vector equation...Ch. 1.3 - In Exercises 11 and 12, determine if b is a linear...Ch. 1.3 - In Exercises 11 and 12, determine if b is a linear...Ch. 1.3 - In Exercises 13 and 14, determine if b is a linear...Ch. 1.3 - In Exercises 13 and 14, determine if b is a linear...Ch. 1.3 - In Exercises 15 and 16, list five vectors in Span...Ch. 1.3 - In Exercises 15 and 16, list five vectors in Span...Ch. 1.3 - Let a1=[142],a2=[237],andb=[41h]. For what...Ch. 1.3 - Let v1=[102],v2=[318],andy=[h53]. For what...Ch. 1.3 - Give a geometric description of Span {v1, v2} for...Ch. 1.3 - Give a geometric description of Span {v1, v2} for...Ch. 1.3 - Let u=[21]andv=[21]. Show that [hk] is an Span {u,...Ch. 1.3 - Construct a 3 3 matrix A, with nonzero entries,...Ch. 1.3 - a. Another notation for the vector [43] is [-4 3]....Ch. 1.3 - a. Any list of five real numbers is a vector in 5....Ch. 1.3 - Let A = [104032263] and b = [414]. Denote the...Ch. 1.3 - Let A = [206185121], let b = [1033], let W be the...Ch. 1.3 - A mining company has two mines. One days operation...Ch. 1.3 - A steam plain bums two types of coal: anthracite...Ch. 1.3 - Let v1, vk be points in 3 and suppose that for j...Ch. 1.3 - Let v be the center of mass of a system of point...Ch. 1.3 - A thin triangular plate of uniform density and...Ch. 1.3 - Consider the vectors v1, v2, v3, and b in 2, shown...Ch. 1.3 - Use the vectors u = (u1, , un), v = (v1, , vn),...Ch. 1.3 - Use the vector u = (u1, , un) to verify the...Ch. 1.4 - Let A = [152031954817], P = [3204], and b = [790]....Ch. 1.4 - Let A = [2531], u = [41], and v = [35]. Verify...Ch. 1.4 - Construct a 3 3 matrix A and vectors b and c in 3...Ch. 1.4 - Compute the products in Exercises 1-4 using (a)...Ch. 1.4 - Compute the products in Exercises 1-4 using (a)...Ch. 1.4 - Compute the products in Exercises 1-4 using (a)...Ch. 1.4 - Compute the products in Exercises 1-4 using (a)...Ch. 1.4 - In Exercises 5-8, use the definition of Ax to...Ch. 1.4 - In Exercises 5-8, use the definition of Ax to...Ch. 1.4 - In Exercises 5-8, use the definition of Ax to...Ch. 1.4 - In Exercises 5-8, use the definition of Ax to...Ch. 1.4 - In Exercises 9 and 10, write the system first as a...Ch. 1.4 - In Exercises 9 and 10, write the system first as a...Ch. 1.4 - Given A and b in Exercises 11 and 12, write the...Ch. 1.4 - Given A and b in Exercises 11 and 12, write the...Ch. 1.4 - Let u = [044] and A = [352611]. Is u in the plane...Ch. 1.4 - Let u = [232] and A = [587011130]. Is u in the...Ch. 1.4 - Let A = [2163] and b = [b1b2]. Show that the...Ch. 1.4 - Repeat Exercise 15: A = [134326518], b = [b1b2b3]....Ch. 1.4 - Exercises 17-20 refer to the matrices A and B...Ch. 1.4 - Exercises 17-20 refer to the matrices A and B...Ch. 1.4 - Exercises 17-20 refer to the matrices A and B...Ch. 1.4 - Exercises 17-20 refer to the matrices A and B...Ch. 1.4 - Let v1 = [1010], v2 = [0101], v3 = [1001]. Does...Ch. 1.4 - Let v1 = [002], v2 = [038], v3 = [415]. Does {v1,...Ch. 1.4 - a. The equation Ax = b is referred to as a vector...Ch. 1.4 - a. Every matrix equation Ax = b corresponds to a...Ch. 1.4 - Note that [431525623][312]=[7310]. Use this fact...Ch. 1.4 - Let u = [725], v = [313], and w = [610]. It can be...Ch. 1.4 - Let q1, q2, q3, and v represent vectors in 5, and...Ch. 1.4 - Rewrite the (numerical) matrix equation below in...Ch. 1.4 - Construct a 3 3 matrix, not in echelon form,...Ch. 1.4 - Construct a 3 3 matrix, not in echelon form,...Ch. 1.4 - Let A be a 3 2 matrix. Explain why the equation...Ch. 1.4 - Could a set of three vectors in 4 span all of 4?...Ch. 1.4 - Suppose A is a 4 3 matrix and b is a vector in 4...Ch. 1.4 - Suppose A is a 3 3 matrix and b is a vector in 3...Ch. 1.4 - Let A be a 3 4 matrix, let y1 and y2 be vectors...Ch. 1.4 - Let A be a 5 3 matrix, let y be a vector in 3,...Ch. 1.4 - [M] In Exercises 37-40, determine if the columns...Ch. 1.4 - [M] In Exercises 37-40, determine if the columns...Ch. 1.4 - [M] In Exercises 37-40, determine if the columns...Ch. 1.4 - [M] In Exercises 37-40, determine if the columns...Ch. 1.5 - Each of the following equations determines a plane...Ch. 1.5 - Write the general solution of 10x1 3x2 2x3 = 7...Ch. 1.5 - Prove the first pan of Theorem 6: Suppose that p...Ch. 1.5 - In Exercises 1-4, determine if the system has a...Ch. 1.5 - In Exercises 1-4, determine if the system has a...Ch. 1.5 - In Exercises 1-4, determine if the system has a...Ch. 1.5 - In Exercises 1-4, determine if the system has a...Ch. 1.5 - In Exercises 5 and 6, follow the method of...Ch. 1.5 - In Exercises 5 and 6, follow the method of...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - In Exercises 7-12, describe all solutions of Ax =...Ch. 1.5 - Suppose the solution set of a certain system of...Ch. 1.5 - Suppose the solution set of a certain system of...Ch. 1.5 - Follow the method of Example 3 to describe the...Ch. 1.5 - As in Exercise 15, describe the solutions of the...Ch. 1.5 - Describe and compare the solution sets of x1 + 9x2...Ch. 1.5 - Describe and compare the solution sets of x1 3x2...Ch. 1.5 - In Exercises 19 and 20, find the parametric...Ch. 1.5 - In Exercises 19 and 20, find the parametric...Ch. 1.5 - In Exercises 21 and 22, find a parametric equation...Ch. 1.5 - In Exercises 21 and 22, find a parametric equation...Ch. 1.5 - a. A homogeneous equation is always consistent. b....Ch. 1.5 - a. If x is a nontrivial solution of Ax = 0, then...Ch. 1.5 - Prove the second part of Theorem 6: Let w be any...Ch. 1.5 - Suppose Ax = b has a solution. Explain why the...Ch. 1.5 - Suppose A is the 3 3 zero matrix (with all zero...Ch. 1.5 - If b 0, can the solution set of Ax = b be a plane...Ch. 1.5 - In Exercises 29-32, (a) does the equation Ax = 0...Ch. 1.5 - In Exercises 29-32, (a) does the equation Ax = 0...Ch. 1.5 - In Exercises 29-32, (a) does the equation Ax = 0...Ch. 1.5 - In Exercises 29-32, (a) does the equation Ax = 0...Ch. 1.5 - Given A = [2672139], find one nontrivial solution...Ch. 1.5 - Given A = [4681269], find one nontrivial solution...Ch. 1.5 - Construct a 3 3 nonzero matrix A such that the...Ch. 1.5 - Construct a 3 3 nonzero matrix A such that the...Ch. 1.5 - Construct a 2 2 matrix A such that the solution...Ch. 1.5 - Suppose A is a 3 3 matrix and y is a vector in 3...Ch. 1.5 - Let A be an m n matrix and let u be a vector in n...Ch. 1.5 - Let A be an m n matrix, and let u and v be...Ch. 1.6 - Suppose an economy has three sectors: Agriculture,...Ch. 1.6 - Consider the network flow studied in Example 2....Ch. 1.6 - Suppose an economy has only two sectors, Goods and...Ch. 1.6 - Find another set of equilibrium prices for the...Ch. 1.6 - Boron sulfide reacts violently with water to form...Ch. 1.6 - When solutions of sodium phosphate and barium...Ch. 1.6 - Alka-Seltzer contains sodium bicarbonate (NaHCO3)...Ch. 1.6 - The following reaction between potassium...Ch. 1.6 - Find the general flow pattern of the network shown...Ch. 1.6 - a. Find the general traffic pattern in the freeway...Ch. 1.6 - a. Find the general flow pattern in the network...Ch. 1.6 - Intersections in England are often constructed as...Ch. 1.7 - Let u = [324] , v = [617] , w = [052] , and z =...Ch. 1.7 - Suppose that {v1, v2, v3} is a linearly dependent...Ch. 1.7 - In Exercises 1-4, determine if the vectors are...Ch. 1.7 - In Exercises 1-4, determine if the vectors are...Ch. 1.7 - In Exercises 1-4, determine if the vectors are...Ch. 1.7 - In Exercises 1-4, determine if the vectors are...Ch. 1.7 - In Exercises 5-8, determine if the columns of the...Ch. 1.7 - In Exercises 5-8, determine if the columns of the...Ch. 1.7 - In Exercises 5-8, determine if the columns of the...Ch. 1.7 - In Exercises 5-8, determine if the columns of the...Ch. 1.7 - In Exercises 9 and 10, (a) for what values of h is...Ch. 1.7 - In Exercises 9 and 10, (a) for what values of h is...Ch. 1.7 - In Exercises 11-14, find the value(s) of h for...Ch. 1.7 - In Exercises 11-14, find the value(s) of h for...Ch. 1.7 - In Exercises 11-14, find the value(s) of h for...Ch. 1.7 - In Exercises 11-14, find the value(s) of h for...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - Determine by inspection whether the vectors in...Ch. 1.7 - In Exercises 21 and 22, mark each statement True...Ch. 1.7 - In Exercises 21 and 22, mark each statement True...Ch. 1.7 - In Exercises 23-26, describe the possible echelon...Ch. 1.7 - In Exercises 23-26, describe the possible echelon...Ch. 1.7 - In Exercises 23-26, describe the possible echelon...Ch. 1.7 - In Exercises 23-26, describe the possible echelon...Ch. 1.7 - How many pivot columns must a 7 5 matrix have if...Ch. 1.7 - How many pivot columns must a 5 7 matrix have if...Ch. 1.7 - Construct 3 2 matrices A and B such that Ax = 0...Ch. 1.7 - a. Fill in the blank in the following statement:...Ch. 1.7 - Exercises 31 and 32 should be solved without...Ch. 1.7 - Exercises 31 and 32 should be solved without...Ch. 1.7 - Each statement in Exercises 33-38 is either true...Ch. 1.7 - Each statement in Exercises 33-38 is either true...Ch. 1.7 - Each statement in Exercises 33-38 is either true...Ch. 1.7 - Each statement in Exercises 33-38 is either true...Ch. 1.7 - Each statement in Exercises 33-38 is either true...Ch. 1.7 - Each statement in Exercises 33-38 is either true...Ch. 1.7 - Suppose A is an m n matrix with the property that...Ch. 1.7 - Suppose an m n matrix A has n pivot columns....Ch. 1.7 - [M] In Exercises 41 and 42, use as many columns of...Ch. 1.7 - [M] In Exercises 41 and 42, use as many columns of...Ch. 1.8 - Suppose T : 5 2 and T(x) = Ax for some matrix A...Ch. 1.8 - A=[1001] Give a geometric description of the...Ch. 1.8 - The line segment from 0 to a vector u is the set...Ch. 1.8 - Let A=[2002], and define T : 22 by T(x) = Ax. Find...Ch. 1.8 - Let A=[.5000.5000.5], u=[104], and v=[abc]. Define...Ch. 1.8 - In Exercises 3-6, with T defined by T(x) = Ax,...Ch. 1.8 - In Exercises 3-6, with T defined by T(x) = Ax,...Ch. 1.8 - In Exercises 3-6, with T defined by T(x) = Ax,...Ch. 1.8 - In Exercises 3-6, with T defined by T(x) = Ax,...Ch. 1.8 - Let A be a 6 5 matrix. What must a and b be in...Ch. 1.8 - How many rows and columns must a matrix A have in...Ch. 1.8 - For Exercises 9 and 10, find all x in 4 that are...Ch. 1.8 - For Exercises 9 and 10, find all x in 4 that are...Ch. 1.8 - Let b=[110], and let A be the matrix in Exercise...Ch. 1.8 - Let b=[1314]. and let A be the matrix in Exercise...Ch. 1.8 - In Exercises 13-16, use a rectangular coordinate...Ch. 1.8 - In Exercises 13-16, use a rectangular coordinate...Ch. 1.8 - In Exercises 13-16, use a rectangular coordinate...Ch. 1.8 - In Exercises 13-16, use a rectangular coordinate...Ch. 1.8 - Let T : 2 2 be a linear transformation that maps...Ch. 1.8 - The figure shows vectors u, v, and w, along with...Ch. 1.8 - Let e1=[10], e2=[01], y1=[25], and y2=[16], and...Ch. 1.8 - Let x=[x1x2], v1=[25], and v2=[73], and let T : 2 ...Ch. 1.8 - In Exercises 21 and 22, mark each statement True...Ch. 1.8 - In Exercises 21 and 22, mark each statement True...Ch. 1.8 - Let T : 2 2 be the linear transformation that...Ch. 1.8 - Suppose vectors v1, . . . , vp span n, and let T :...Ch. 1.8 - Prob. 25ECh. 1.8 - Let u and v be linearly independent vectors in 3,...Ch. 1.8 - Prob. 27ECh. 1.8 - Let u and v be vectors in n. It can be shown that...Ch. 1.8 - Define f : by f(x) = mx + b. a. Show that f is...Ch. 1.8 - An affine transformation T : n m has the form...Ch. 1.8 - Let T : n m be a linear transformation, and let...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - In Exercises 32-36, column vectors are written as...Ch. 1.8 - [M] In Exercises 37 and 38, the given matrix...Ch. 1.8 - [M] In Exercises 37 and 38, the given matrix...Ch. 1.8 - [M] Let b=[7597] and let A be the matrix in...Ch. 1.8 - [M] Let b=[77135] and let A be the matrix in...Ch. 1.9 - Let T : 2 2 be the transformation that first...Ch. 1.9 - Suppose A is a 7 5 matrix with 5 pivots. Let T(x)...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - In Exercises 1-10, assume that T is a linear...Ch. 1.9 - A linear transformation T : 2 2 first reflects...Ch. 1.9 - Show that the transformation in Exercise 8 is...Ch. 1.9 - Let T : 2 be the linear transformation such that...Ch. 1.9 - Let T : 2 2 be a linear transformation with...Ch. 1.9 - In Exercises 15 and 16, fill in the missing...Ch. 1.9 - In Exercises 15 and 16, fill in the missing...Ch. 1.9 - In Exercises 17-20, show that T is a linear...Ch. 1.9 - In Exercises 17-20, show that T is a linear...Ch. 1.9 - In Exercises 17-20, show that T is a linear...Ch. 1.9 - In Exercises 17-20, show that T is a linear...Ch. 1.9 - Let T : 2 2 be a linear transformation such that...Ch. 1.9 - Let T : 2 3 be a linear transformation such that...Ch. 1.9 - In Exercises 23 and 24, mark each statement True...Ch. 1.9 - a. Not every linear transformation from n to m is...Ch. 1.9 - In Exercises 25-28, determine if the specified...Ch. 1.9 - In Exercises 25-28, determine if the specified...Ch. 1.9 - In Exercises 25-28, determine if the specified...Ch. 1.9 - In Exercises 25-28, determine if the specified...Ch. 1.9 - In Exercises 29 and 30, describe the possible...Ch. 1.9 - In Exercises 29 and 30, describe the possible...Ch. 1.9 - Let T : n m be a linear transformation, with A...Ch. 1.9 - Let T : n m be a linear transformation, with A...Ch. 1.9 - Verify the uniqueness of A in Theorem 10. Let T :...Ch. 1.9 - Why is the question Is the linear transformation T...Ch. 1.9 - If a linear transformation T : n m maps n onto m,...Ch. 1.9 - Let S : p n and T : n m be linear...Ch. 1.9 - [M] In Exercises 37-40, let T be the linear...Ch. 1.9 - [M] In Exercises 37-40, let T be the linear...Ch. 1.9 - [M] In Exercises 37-40, let T be the linear...Ch. 1.9 - [M] In Exercises 37-40, let T be the linear...Ch. 1.10 - Find a matrix A and vectors x and b such that the...Ch. 1.10 - The container of a breakfast cereal usually lists...Ch. 1.10 - One serving of Post Shredded Wheat supplies 160...Ch. 1.10 - After taking a nutrition class, a big Annies Mac...Ch. 1.10 - The Cambridge Diet supplies .8 g of calcium per...Ch. 1.10 - In Exercises 5-8, write a matrix equation that...Ch. 1.10 - In Exercises 5-8, write a matrix equation that...Ch. 1.10 - In Exercises 5-8, write a matrix equation that...Ch. 1.10 - In Exercises 5-8, write a matrix equation that...Ch. 1.10 - In a certain region, about 7% of a citys...Ch. 1.10 - In a certain region, about 6% of a citys...Ch. 1.10 - In 2012 the population of California was...Ch. 1.10 - [M] Budget Rent A Car in Wichita. Kansas, has a...Ch. 1.10 - [M] Let M and xo be as in Example 3. a. Compute...Ch. 1.10 - [M] Study how changes in boundary temperatures on...Ch. 1 - Mark each statement True or False. Justify each...Ch. 1 - Let a and b represent real numbers. Describe the...Ch. 1 - The solutions (x, y, Z) of a single linear...Ch. 1 - Suppose the coefficient matrix of a linear system...Ch. 1 - Determine h and k such that the solution set of...Ch. 1 - Consider the problem of determining whether the...Ch. 1 - Consider the problem of determining whether the...Ch. 1 - Describe the possible echelon forms of the matrix...Ch. 1 - Prob. 9SECh. 1 - Let a1, a2 and b be the vectors in 2 shown in the...Ch. 1 - Construct a 2 3 matrix A, not in echelon form,...Ch. 1 - Construct a 2 3 matrix A, not in echelon form,...Ch. 1 - Write the reduced echelon form of a 3 3 matrix A...Ch. 1 - Determine the value(s) of a such that...Ch. 1 - In (a) and (b), suppose the vectors are linearly...Ch. 1 - Use Theorem 7 in Section 1.7 to explain why the...Ch. 1 - Explain why a set {v1, v2, v3, v4} in 5 must be...Ch. 1 - Suppose {v1, v2} is a linearly independent set in...Ch. 1 - Suppose v1, v2, v3 are distinct points on one line...Ch. 1 - Let T : n m be a linear transformation, and...Ch. 1 - Let T : 3 3 be the linear transformation that...Ch. 1 - Let A be a 3 3 matrix with the property that the...Ch. 1 - A Givens rotation is a linear transformation from...Ch. 1 - The following equation describes a Givens rotation...Ch. 1 - A large apartment building is to be built using...

Additional Math Textbook Solutions

Find more solutions based on key concepts
NOTE: Write your answers using interval notation when appropriate. CHECKING ANALYTIC SKILLS Fill in each blank ...

Graphical Approach To College Algebra

The value of x for the given equation.

Intermediate Algebra (7th Edition)

Solve each formula for the given letter . [2.3] What percent of 60 is 42? [2.4]

Elementary and Intermediate Algebra

Fill in each blanks so that the resulting statement is true. Any set of ordered pairs is called a/an _______. T...

College Algebra (7th Edition)

Practice Exercises In Exercises 1—20, find all numbers for which each rational expression is undefined. If th...

Introductory and Intermediate Algebra for College Students (5th Edition)

NOTE: Write your answers using interval notation when appropriate. CHECKING ANALYTIC SKILLS Fill in each blank ...

A Graphical Approach to College Algebra (6th Edition)

Knowledge Booster
Background pattern image
Algebra
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Text book image
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
SEE MORE TEXTBOOKS
Linear Transformations on Vector Spaces; Author: Professor Dave Explains;https://www.youtube.com/watch?v=is1cg5yhdds;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY