Chapter 1.3, Problem 29E

Let v₁, … v_k be points in ℝ³ and suppose that for j = 1, … , k an object with mass m_j is located at point v_j. Physicists call such objects point masses. The total mass of the system of point masses is

m = m₁ + … + m_k

The center of gravity (or center of mass) of the system is

$\bar{\text{v}}=\frac{1}{m}\left[m_1{\text{v}}_1+\cdots +m_k{\text{v}}_k\right]$

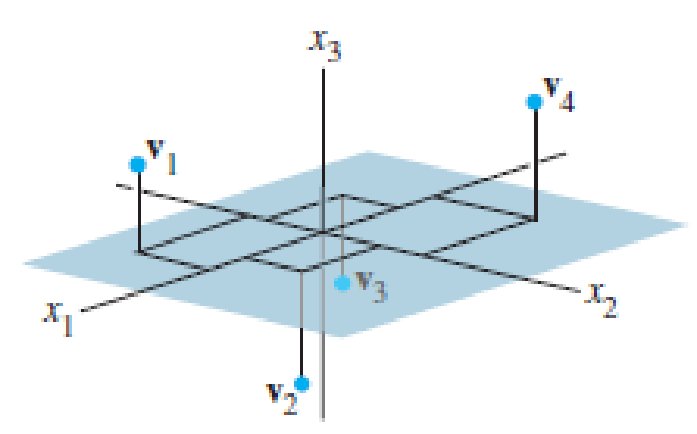
Compute the center of gravity of the system consisting of the following point masses (see the figure):

Point	Mass
v1 =(5, −4, 3)	2 g
v2 = (4, 3, −2)	5 g
v3 = (−4, −3, −1)	2 g
v4 = (−9, 8, 6)	1 g