
(a)
To show: The stationary line is at distance of
(a)
Answer to Problem 44CP
The distance at which stationary line lie is
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
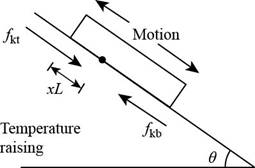
Figure 1
Consider that
The normal force on the lower part of the plane is,
Here,
The force due to gravity is,
The equation for the
The equation for the downward force is,
The force equation for the plate is,
Further, solve for
The distance of the stationary line below the top edge is,
Conclusion:
Therefore, the distance at which stationary line lie is
(b)
To show: The stationary line is at that same distance above the bottom edge of the plate.
(b)
Answer to Problem 44CP
The stationary line is at that same distance above the bottom edge of the plate.
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
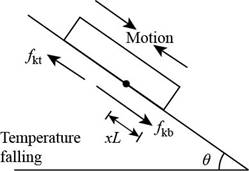
Figure 2
With the temperature falling, the plate contracts faster than the roof. The upper part slides down and feels an upward frictional force,
Then the force equation remains same as in part (a) and the stationary line is above the bottom edge by,
Conclusion:
Therefore, it is proved that the stationary line is at that same distance above the bottom edge of the plate.
(c)
To show: The plate steps down the roof like an inchworm moving each day by the distance
(c)
Answer to Problem 44CP
The distance by which the plate steps down the roof like an inchworm moving each day is
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
Consider the figure given below.
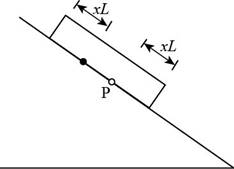
Figure 3
Consider the plate at dawn, as the temperature starts to rise. As in part (a), a line at distance
In the above figure, the point
The change in the length of the plate is,
The change in the length of the roof is,
The point on the roof originally under point
When the temperature drops, point
The displacement for a day is,
Substitute
Conclusion:
Therefore, the distance by which the plate steps down the roof like an inchworm moving each day is
(d)
The distance an aluminum plate moves each day.
(d)
Answer to Problem 44CP
The distance an aluminum plate moves each day is
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
The length of the plate is
The coefficient of linear expansion for aluminum is
The formula for the displacement for a day is,
Substitute
Conclusion:
Therefore, the distance an aluminum plate moves each day is
(e)
To explain: The effect on the plate if the expansion coefficient of the plate is less than the expansion coefficient of the roof.
(e)
Answer to Problem 44CP
The plate creeps down the roof each day by an amount given by
Explanation of Solution
Given info: The angle made by the roof with the horizontal plane is
If
The figure I, applies to the temperature falling and figure II applies to temperature rising. A point on the plate
The plate creeps down the roof each day by an amount given by,
Conclusion:
Therefore, the plate creeps down the roof each day by an amount given by
Want to see more full solutions like this?
Chapter 18 Solutions
Physics for Scientists and Engineers with Modern Physics
- a) Consider the following function, where A is a constant. y(x,t) = A(x — vt). Can this represent a wave that travels along? Explain. b) Which of the following are possible traveling waves, provide your reasoning and give the velocity of the wave if it can be a traveling wave. e-(a²x²+b²²-2abtx b.1) y(x,t) b.2) y(x,t) = = A sin(ax² - bt²). 2 b.3) y(x,t) = A sin 2π (+) b.4) y(x,t) = A cos² 2π(t-x). b.5) y(x,t) = A cos wt sin(kx - wt)arrow_forwardThe capacitor in (Figure 1) is initially uncharged. The switch is closed at t=0. Immediately after the switch is closed, what is the current through the resistor R1, R2, and R3? What is the final charge on the capacitor? Please explain all steps.arrow_forwardSuppose you have a lens system that is to be used primarily for 620-nm light. What is the second thinnest coating of fluorite (calcium fluoride) that would be non-reflective for this wavelength? × nm 434arrow_forward
- The angle between the axes of two polarizing filters is 19.0°. By how much does the second filter reduce the intensity of the light coming through the first? I = 0.106 40 xarrow_forwardAn oil slick on water is 82.3 nm thick and illuminated by white light incident perpendicular to its surface. What color does the oil appear (what is the most constructively reflected wavelength, in nanometers), given its index of refraction is 1.43? (Assume the index of refraction of water is 1.33.) wavelength color 675 × nm red (1 660 nm)arrow_forwardA 1.50 μF capacitor is charging through a 16.0 Ω resistor using a 15.0 V battery. What will be the current when the capacitor has acquired 1/4 of its maximum charge? Please explain all stepsarrow_forward
- In the circuit shown in the figure (Figure 1), the 6.0 Ω resistor is consuming energy at a rate of 24 J/s when the current through it flows as shown. What are the polarity and emf of the battery E, assuming it has negligible internal resistance? Please explain all steps. I know you need to use the loop rule, but I keep getting the answer wrong.arrow_forwardIf you connect a 1.8 F and a 2.6 F capacitor in series, what will be the equivalent capacitance?arrow_forwardSuppose that a particular heart defibrillator uses a 1.5 x 10-5 Farad capacitor. If it is charged up to a voltage of 7300 volts, how much energy is stored in the capacitor? Give your answer as the number of Joules.arrow_forward
- The voltage difference across an 8.3 nanometer thick cell membrane is 6.5 x 10-5volts. What is the magnitude of the electric field inside this cell membrane? (Assume the field is uniform, and give your answer as the number of Volts per meter... which is the same as the number of Newtons per Coulomb.)arrow_forwardThree identical capacitors are connected in parallel. When this parallel assembly of capacitors is connected to a 12 volt battery, a total of 3.1 x 10-5 coulombs flows through the battery. What is the capacitance of one individual capacitor? (Give your answer as the number of Farads.)arrow_forwardSuppose you construct your own capacitor by placing two parallel plates at a distance 0.27 meters apart. The plates each have a surface area of 0.64 square meters. What is the capacitance of this setup? (Give your answer as the number of Farads.)arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





