Chapter 17.1, Problem 17.16P

A slender rod of length l and mass m is pivoted about a point C located at a distance b from its center G. It is released from rest in a horizontal position and swings freely. Determine (a) the angular velocity of the rod as it passes through a vertical position if b = l/2, (b) the distance b for which the angular velocity of the rod as it passes through a vertical position is maximum, (c) the corresponding values of its angular velocity and of the reaction at C using the value of b calculated.

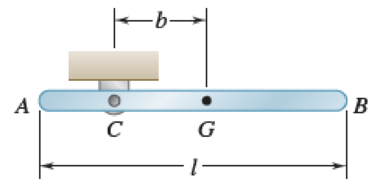
Fig. P17.16

To determine

Find the angular velocity of the rod when $b=l/2$.

Answer to Problem 17.16P

The angular velocity of the rod when $b=l/2$ is $\underset{\_}{{\omega }_2=\sqrt{\frac{3g}{l}}\left(\text{clockwise}\right)}$.

Explanation of Solution

Show the free-body diagram of the given condition as in Figure 1.

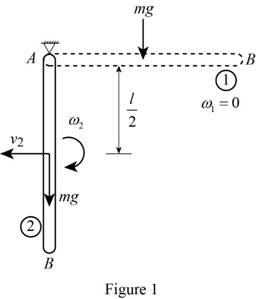
Find the mass moment of inertia of the slender rod $\left(\overline{I}\right)$ using the relation.

$\overline{I}=\frac{m{l}^2}{12}$

Here, the mass of the slender rod is m and the length of the slender rod is l.

Position 1 (Horizontal position):

The angular velocity $\left({\omega }_1\right)$ in the horizontal position is zero.

${\omega }_1=0$

The velocity $\left(v_1\right)$ of the slender rod at the horizontal position is zero.

${\overline{v}}_1=0$

Find the total kinetic energy in the horizontal position $\left(T_1\right)$ using the relation.

$T_1=\frac{1}{2}m{\overline{v}}_1^2+\frac{1}{2}\overline{I}{\omega }_1^2$

Substitute 0 for ${\overline{v}}_1$ and 0 for ${\omega }_1$.

$\begin{array}{c}{T}_1=\frac{1}{2}m{\left(0\right)}^2+\frac{1}{2}\overline{I}{\left(0\right)}^2\\ =0\end{array}$

Positon 2 (Vertical position):

Find the velocity of the slender rod $\left({\overline{v}}_2\right)$ at the final position using the relation.

${\overline{v}}_2=\frac{l}{2}{\omega }_2$

Find the total kinetic energy in the vertical position $\left(T_2\right)$ using the relation.

$T_2=\frac{1}{2}m{\overline{v}}_2^2+\frac{1}{2}\overline{I}{\omega }_2^2$

Substitute $\frac{l}{2}{\omega }_2$ for ${\overline{v}}_2$ and $\frac{m{l}^2}{12}$ for $\overline{I}$.

$\begin{array}{c}{T}_2=\frac{1}{2}m{\left(\frac{l}{2}{\omega }_2\right)}^2+\frac{1}{2}\left(\frac{m{l}^2}{12}\right){\omega }_2^2\\ =\frac{m{l}^2{\omega }_2^2}{8}+\frac{m{l}^2{\omega }_2^2}{24}\\ =\frac{m{l}^2{\omega }_2^2}{6}\end{array}$

Find the work done $\left(U_{1\to 2}\right)$ for the rigid body using the relation;

$U_{1\to 2}=mg\times \frac{l}{2}$

Here, the acceleration due to gravity is g.

Write the equation of work and energy for the system using the equation.

$T_1+U_{1\to 2}=T_2$

Substitute 0 for $T_1$, $mg\times \frac{l}{2}$ for $U_{1\to 2}$, and $\frac{m{l}^2{\omega }_2^2}{6}$ for $T_2$

$\begin{array}{l}0+mg\times \frac{l}{2}=\frac{m{l}^2{\omega }_2^2}{6}\\ {\omega }_2^2=\frac{3g}{l}\\ {\omega }_2=\sqrt{\frac{3g}{l}}\left(\text{clockwise}\right)\end{array}$

Therefore, the angular velocity of the rod when $b=l/2$ is $\underset{\_}{{\omega }_2=\sqrt{\frac{3g}{l}}\left(\text{clockwise}\right)}$.

To determine

Find the distance b for which the angular velocity of rod as it passes through a vertical position is maximum.

Answer to Problem 17.16P

The distance b for which the angular velocity of the rod is maximum in vertical position is $\underset{\_}{\frac{l}{\sqrt{12}}}$.

Explanation of Solution

Position 1 (Horizontal position):

Show the free-body diagram of the horizontal position as in Figure 2.

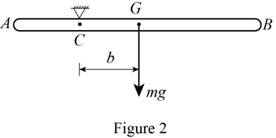
Find the mass moment of inertia of the slender rod $\left(\overline{I}\right)$ using the relation.

$\overline{I}=\frac{m{l}^2}{12}$

The angular velocity $\left({\omega }_1\right)$ in the horizontal position is zero.

${\omega }_1=0$

The velocity $\left(v_1\right)$ of the slender rod at the horizontal position is zero.

${\overline{v}}_1=0$

Find the total kinetic energy in the horizontal position $\left(T_1\right)$ using the relation.

$T_1=\frac{1}{2}m{\overline{v}}_1^2+\frac{1}{2}\overline{I}{\omega }_1^2$

Substitute 0 for ${\overline{v}}_1$ and 0 for ${\omega }_1$.

$\begin{array}{c}{T}_1=\frac{1}{2}m{\left(0\right)}^2+\frac{1}{2}\overline{I}{\left(0\right)}^2\\ =0\end{array}$

The elevation (h) of the pivot C is zero.

$h=0$

Find the total potential energy $\left(V_1\right)$  at the horizontal position using the relation.

$V_1=mgh$

Substitute 0 for h.

$\begin{array}{c}{V}_1=mg\left(0\right)\\ =0\end{array}$

Positon 2 (Vertical position):

Show the free-body diagram of the vertical position as in Figure 3.

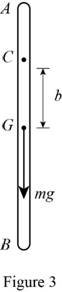
Find the velocity of the slender rod $\left({\overline{v}}_2\right)$ at the final position using the relation.

${\overline{v}}_2=b{\omega }_2$

Find the total kinetic energy in the vertical position $\left(T_2\right)$ using the relation.

$T_2=\frac{1}{2}m{\overline{v}}_2^2+\frac{1}{2}\overline{I}{\omega }_2^2$

Substitute $b{\omega }_2$ for ${\overline{v}}_2$ and $\frac{m{l}^2}{12}$ for $\overline{I}$.

$\begin{array}{c}{T}_2=\frac{1}{2}m{\left(b{\omega }_2\right)}^2+\frac{1}{2}\left(\frac{m{l}^2}{12}\right){\omega }_2^2\\ =\frac{m{b}^2{\omega }_2^2}{2}+\frac{m{l}^2{\omega }_2^2}{24}\end{array}$

The elevation of the pivot C is $h=-b$.

Find the total potential energy $\left(V_2\right)$ at the vertical position using the relation.

$V_2=mgh$

Substitute ­b for h.

$V_2=-mgb$

Write the equation of conservation of energy using the equation.

$T_1+V_1=T_2+V_2$

Substitute 0 for $T_1$, 0 for $V_1$, $\left(\frac{m{b}^2{\omega }_2^2}{2}+\frac{m{l}^2{\omega }_2^2}{24}\right)$ for $T_2$, and $-mgb$ for $V_2$.

$\begin{array}{l}0+0=\frac{m{b}^2{\omega }_2^2}{2}+\frac{m{l}^2{\omega }_2^2}{24}-mgb\\ 12b^2{\omega }_2^2+l^2{\omega }_2^2-24gb=0\\ {\omega }_2^2\left(12b^2+l^2\right)-24gb=0\\ {\omega }_2^2=\frac{24gb}{12b^2+l^2}\end{array}$ (1)

Integrate the angular velocity with respect to b and equate to zero.

$\begin{array}{c}\frac{d{\omega }_2^2}{db}=0\\ \frac{d\left(\frac{24gb}{12b^2+l^2}\right)}{db}=0\\ \frac{\left(12b^2+l^2\right)-b\left(24b\right)}{{\left(12b^2+l^2\right)}^2}=0\\ 12b^2+l^2-24b^2=0\end{array}$

$\begin{array}{c}-12b^2+l^2=0\\ b^2=\frac{l^2}{12}\\ b=\frac{l}{\sqrt{12}}\end{array}$

Therefore, the distance b for which the angular velocity of the rod is maximum in vertical position is $\underset{\_}{\frac{l}{\sqrt{12}}}$.

To determine

Find the angular velocity where the vertical position is maximum and the reaction at pivot C.

Answer to Problem 17.16P

The angular velocity corresponding to the maximum vertical position is $\underset{\_}{{\omega }_2=1.861\sqrt{\frac{g}{l}}\left(\text{clockwise}\right)}$.

The reaction at pivot C is $\underset{\_}{C=2mg(\uparrow )}$.

Explanation of Solution

Refer to the calculation of part (b):

Substitute $\frac{l}{\sqrt{12}}$ for b in Equation (1).

$\begin{array}{c}{\omega }_2^2=\frac{24g\left(\frac{l}{\sqrt{12}}\right)}{12{\left(\frac{l}{\sqrt{12}}\right)}^2+l^2}\\ =\frac{24gl}{\frac{12\sqrt{12}{l}^2}{12}+\sqrt{12}{l}^2}\\ =\frac{24g}{\sqrt{12}l+\sqrt{12}l}\\ =\frac{2\times \sqrt{12}\times \sqrt{12}g}{2\sqrt{12}l}\end{array}$

$\begin{array}{c}{\omega }_2=\sqrt{\frac{\sqrt{12}g}{l}}\\ ={\left(12\right)}^{\frac{1}{4}}\sqrt{\frac{g}{l}}\\ =1.861\sqrt{\frac{g}{l}}\left(\text{clockwise}\right)\end{array}$

Therefore, the angular velocity corresponding to the maximum vertical position is $\underset{\_}{{\omega }_2=1.861\sqrt{\frac{g}{l}}\left(\text{clockwise}\right)}$.

Show the free-body diagram of the slender rod as in Figure 4.

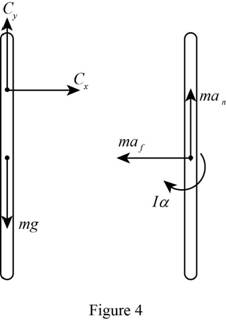
Find the normal acceleration $\left(a_n\right)$ using the relation.

$a_n=b{\omega }_2^2$

Substitute $\frac{l}{\sqrt{12}}$ for b and ${\left(12\right)}^{\frac{1}{4}}\sqrt{\frac{g}{l}}$ for ${\omega }_2$.

$\begin{array}{c}{a}_n=\frac{l}{\sqrt{12}}\times {\left({\left(12\right)}^{\frac{1}{4}}\sqrt{\frac{g}{l}}\right)}^2\\ =\frac{l}{\sqrt{12}}\times \frac{\sqrt{12}g}{l}\\ =g\end{array}$

The value of tangential acceleration is $a_f=b\alpha$.

Resolve the vertical component of forces.

$\begin{array}{l}{\displaystyle \sum F_y=0}\\ C_y-mg-m{a}_n=0\\ C_y-mg-mg=0\\ C_y=2mg\end{array}$

Take moment about point C as follows;

$\begin{array}{l}{\displaystyle \sum M_C=0}\\ mb{a}_f+\overline{I}\alpha =0\\ m{b}^2\alpha +\overline{I}\alpha =0\\ \alpha =0\end{array}$

Therefore, $a_f=0$

Resolve the horizontal component of forces.

$\begin{array}{l}{\displaystyle \sum F_x=0}\\ C_x+m{a}_f=0\\ C_x+m\left(0\right)=0\\ C_x=0\end{array}$

Find the resultant reaction at point C using the relation.

$C=\sqrt{C_x^2+C_y^2}$

Substitute 0 for $C_x$ and 2mg for $C_y$.

$\begin{array}{c}C=\sqrt{0^2+{\left(2mg\right)}^2}\\ =2mg(\uparrow )\end{array}$

Therefore, the reaction at pivot C is $\underset{\_}{C=2mg(\uparrow )}$.