High School Math 2015 Common Core Algebra 1 Student Edition Grade 8/9
15th Edition
ISBN: 9780133281149
Author: Prentice Hall
Publisher: Prentice Hall
expand_more
expand_more
format_list_bulleted
Videos
Question
Chapter 1.7, Problem 6LC
a)
To determine
To find:
A set of ordered pairs representing table data in ordered pair form
a)
Expert Solution
Answer to Problem 6LC
Required ordered pairs in form
Explanation of Solution
Given information:
Table given below shows the total enrollment in U.S. public school.
Also, x represents school years, 2012-13 onwards and y is the total enrollment
Concept used:
While forming an ordered pair, independent variable is put as first number and dependent variable is put as second number. Further the set of all first values of ordered pair is domain and set of all second numbers is range and if for a relation to be a function, each value of its domain must have a unique value in its co-domain.
Calculation:
Values of x will be taken as 2012, 2013, 2014, 2015 as number of school years, so its related ordered pairs will be
Conclusion:
So, above data in ordered pair form (Year, Enrollment) can be written as:
b)
To determine
To draw:
The related graph between year and enrollment.
b)
Expert Solution
Answer to Problem 6LC
Graph representing the relation between year and enrollment is,
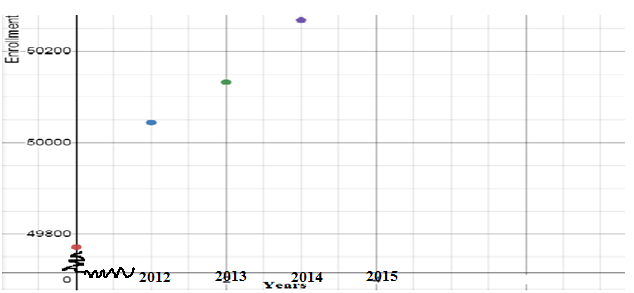
Explanation of Solution
Given information:
Table given below shows the total enrollment in M public school.
Also, , x represents school years, 2012-13 onwards and y is the total enrollment
Concept used:
While forming an ordered pair, independent variable is put as first number and dependent variable is put as second number. Further the set of all first values of ordered pair is domain and set of all second numbers is range and if for a relation to be a function, each value of its domain must have a unique value in its co-domain.
Calculation:
Years will be shown on x axis and enrollment on y axis, while plotting these pairs in XY plane as shown above.
Conclusion:
So, points calculated in ordered pair form, when plotted in XY plane, give the graph as shown above.
c)
To determine
To find:
Domain and range of the data.
c)
Expert Solution
Answer to Problem 6LC
Domain is
Explanation of Solution
Given information:
Table given below shows the total enrollment in M public school.
Also, , x represents school years, 2012-13 onwards and y is the total enrollment
Concept used:
While forming an ordered pair, independent variable is put as first number and dependent variable is put as second number. Further the set of all first values of ordered pair is domain and set of all second numbers is range and if for a relation to be a function, each value of its domain must have a unique value in its co-domain.
Calculation:
As domain is the set of all first numbers of all ordered pairs, so its domain of given relation is
And as for each new first value, there is associated a unique second value in all ordered pairs. So, this relation is surely a function.
Conclusion:
So, as above relation, for each different first value, there is always a unique second value in its given ordered pairs. So, it is surely a function, based on definition of the function.
Chapter 1 Solutions
High School Math 2015 Common Core Algebra 1 Student Edition Grade 8/9
Ch. 1.1 - Prob. 1PCh. 1.1 - Prob. 2PCh. 1.1 - Prob. 3PCh. 1.1 - Prob. 4PCh. 1.1 - Prob. 5PCh. 1.1 - Prob. 1LCCh. 1.1 - Prob. 2LCCh. 1.1 - Prob. 3LCCh. 1.1 - Prob. 4LCCh. 1.1 - Prob. 5LC
Ch. 1.1 - Prob. 6LCCh. 1.1 - Prob. 7LCCh. 1.1 - Prob. 8LCCh. 1.1 - Prob. 9PPECh. 1.1 - Prob. 10PPECh. 1.1 - Prob. 11PPECh. 1.1 - Prob. 12PPECh. 1.1 - Prob. 13PPECh. 1.1 - Prob. 14PPECh. 1.1 - Prob. 15PPECh. 1.1 - Prob. 16PPECh. 1.1 - Prob. 17PPECh. 1.1 - Prob. 18PPECh. 1.1 - Prob. 19PPECh. 1.1 - Prob. 20PPECh. 1.1 - Prob. 21PPECh. 1.1 - Prob. 22PPECh. 1.1 - Prob. 23PPECh. 1.1 - Prob. 24PPECh. 1.1 - Prob. 25PPECh. 1.1 - Prob. 26PPECh. 1.1 - Prob. 27PPECh. 1.1 - Prob. 28PPECh. 1.1 - Prob. 29PPECh. 1.1 - Prob. 30PPECh. 1.1 - Prob. 31PPECh. 1.1 - Prob. 32PPECh. 1.1 - Prob. 33PPECh. 1.1 - Prob. 34PPECh. 1.1 - Prob. 35PPECh. 1.1 - Prob. 36PPECh. 1.1 - Prob. 37PPECh. 1.1 - Prob. 38PPECh. 1.1 - Prob. 39PPECh. 1.1 - Prob. 40PPECh. 1.1 - Prob. 41PPECh. 1.1 - Prob. 1MPCh. 1.2 - Prob. 1PCh. 1.2 - Prob. 2PCh. 1.2 - Prob. 3PCh. 1.2 - Prob. 4PCh. 1.2 - Prob. 1LCCh. 1.2 - Prob. 2LCCh. 1.2 - Prob. 3LCCh. 1.2 - Prob. 4LCCh. 1.2 - Prob. 5LCCh. 1.2 - Prob. 6LCCh. 1.2 - Prob. 7LCCh. 1.2 - Prob. 8LCCh. 1.2 - Prob. 9PPECh. 1.2 - Prob. 10PPECh. 1.2 - Prob. 11PPECh. 1.2 - Prob. 12PPECh. 1.2 - Prob. 13PPECh. 1.2 - Prob. 14PPECh. 1.2 - Prob. 15PPECh. 1.2 - Prob. 16PPECh. 1.2 - Prob. 17PPECh. 1.2 - Prob. 18PPECh. 1.2 - Prob. 19PPECh. 1.2 - Prob. 20PPECh. 1.2 - Prob. 21PPECh. 1.2 - Prob. 22PPECh. 1.2 - Prob. 23PPECh. 1.2 - Prob. 24PPECh. 1.2 - Prob. 25PPECh. 1.2 - Prob. 26PPECh. 1.2 - Prob. 27PPECh. 1.2 - Prob. 28PPECh. 1.2 - Prob. 29PPECh. 1.2 - Prob. 30PPECh. 1.2 - Prob. 31PPECh. 1.2 - Prob. 32PPECh. 1.2 - Prob. 33PPECh. 1.2 - Prob. 34PPECh. 1.2 - Prob. 35PPECh. 1.2 - Prob. 36PPECh. 1.2 - Prob. 37PPECh. 1.2 - Prob. 38PPECh. 1.2 - Prob. 39PPECh. 1.2 - Prob. 40PPECh. 1.2 - Prob. 41PPECh. 1.2 - Prob. 42PPECh. 1.2 - Prob. 43PPECh. 1.2 - Prob. 44PPECh. 1.2 - Prob. 45PPECh. 1.2 - Prob. 46PPECh. 1.2 - Prob. 47PPECh. 1.2 - Prob. 48PPECh. 1.2 - Prob. 49PPECh. 1.2 - Prob. 50PPECh. 1.2 - Prob. 51PPECh. 1.2 - Prob. 52PPECh. 1.2 - Prob. 53PPECh. 1.2 - Prob. 54PPECh. 1.2 - Prob. 55PPECh. 1.2 - Prob. 56PPECh. 1.2 - Prob. 57PPECh. 1.2 - Prob. 58PPECh. 1.2 - Prob. 59PPECh. 1.2 - Prob. 60PPECh. 1.2 - Prob. 61STPCh. 1.2 - Prob. 62STPCh. 1.2 - Prob. 63STPCh. 1.2 - Prob. 64STPCh. 1.2 - Prob. 65MRCh. 1.2 - Prob. 66MRCh. 1.2 - Prob. 67MRCh. 1.2 - Prob. 68MRCh. 1.2 - Prob. 69MRCh. 1.2 - Prob. 70MRCh. 1.2 - Prob. 71MRCh. 1.2 - Prob. 72MRCh. 1.2 - Prob. 73MRCh. 1.2 - Prob. 74MRCh. 1.2 - Prob. 75MRCh. 1.2 - Prob. 76MRCh. 1.2 - Prob. 77MRCh. 1.2 - Prob. 78MRCh. 1.2 - Prob. 79MRCh. 1.2 - Prob. 80MRCh. 1.3 - Prob. 1PCh. 1.3 - Prob. 2PCh. 1.3 - Prob. 3PCh. 1.3 - Prob. 4PCh. 1.3 - Prob. 5PCh. 1.3 - Prob. 1LCCh. 1.3 - Prob. 2LCCh. 1.3 - Prob. 3LCCh. 1.3 - Prob. 4LCCh. 1.3 - Prob. 5LCCh. 1.3 - Prob. 6LCCh. 1.3 - Prob. 7LCCh. 1.3 - Prob. 8LCCh. 1.3 - Prob. 9PPECh. 1.3 - Prob. 10PPECh. 1.3 - Prob. 11PPECh. 1.3 - Prob. 12PPECh. 1.3 - Prob. 13PPECh. 1.3 - Prob. 14PPECh. 1.3 - Prob. 15PPECh. 1.3 - Prob. 16PPECh. 1.3 - Prob. 17PPECh. 1.3 - Prob. 18PPECh. 1.3 - Prob. 19PPECh. 1.3 - Prob. 20PPECh. 1.3 - Prob. 21PPECh. 1.3 - Prob. 22PPECh. 1.3 - Prob. 23PPECh. 1.3 - Prob. 24PPECh. 1.3 - Prob. 25PPECh. 1.3 - Prob. 26PPECh. 1.3 - Prob. 27PPECh. 1.3 - Prob. 28PPECh. 1.3 - Prob. 29PPECh. 1.3 - Prob. 30PPECh. 1.3 - Prob. 31PPECh. 1.3 - Prob. 32PPECh. 1.3 - Prob. 33PPECh. 1.3 - Prob. 34PPECh. 1.3 - Prob. 35PPECh. 1.3 - Prob. 36PPECh. 1.3 - Prob. 37PPECh. 1.3 - Prob. 38PPECh. 1.3 - Prob. 39PPECh. 1.3 - Prob. 40PPECh. 1.3 - Prob. 41PPECh. 1.3 - Prob. 42PPECh. 1.3 - Prob. 43PPECh. 1.3 - Prob. 44PPECh. 1.3 - Prob. 45PPECh. 1.3 - Prob. 46PPECh. 1.3 - Prob. 47PPECh. 1.3 - Prob. 48PPECh. 1.3 - Prob. 49PPECh. 1.3 - Prob. 50PPECh. 1.3 - Prob. 51PPECh. 1.3 - Prob. 52PPECh. 1.3 - Prob. 53PPECh. 1.3 - Prob. 54PPECh. 1.3 - Prob. 55PPECh. 1.3 - Prob. 56PPECh. 1.3 - Prob. 57PPECh. 1.3 - Prob. 58PPECh. 1.3 - Prob. 59PPECh. 1.3 - Prob. 60PPECh. 1.3 - Prob. 61PPECh. 1.3 - Prob. 62PPECh. 1.3 - Prob. 63PPECh. 1.3 - Prob. 64PPECh. 1.3 - Prob. 65PPECh. 1.3 - Prob. 66PPECh. 1.3 - Prob. 67PPECh. 1.3 - Prob. 68PPECh. 1.3 - Prob. 69PPECh. 1.3 - Prob. 70PPECh. 1.3 - Prob. 71PPECh. 1.3 - Prob. 72STPCh. 1.3 - Prob. 73STPCh. 1.3 - Prob. 74STPCh. 1.3 - Prob. 75MRCh. 1.3 - Prob. 76MRCh. 1.3 - Prob. 77MRCh. 1.3 - Prob. 78MRCh. 1.3 - Prob. 79MRCh. 1.3 - Prob. 80MRCh. 1.3 - Prob. 81MRCh. 1.3 - Prob. 82MRCh. 1.3 - Prob. 83MRCh. 1.3 - Prob. 84MRCh. 1.3 - Prob. 85MRCh. 1.4 - Prob. 1PCh. 1.4 - Prob. 2PCh. 1.4 - Prob. 3PCh. 1.4 - Prob. 4PCh. 1.4 - Prob. 1LCCh. 1.4 - Prob. 2LCCh. 1.4 - Prob. 3LCCh. 1.4 - Prob. 4LCCh. 1.4 - Prob. 5LCCh. 1.4 - Prob. 6LCCh. 1.4 - Prob. 7PPECh. 1.4 - Prob. 8PPECh. 1.4 - Prob. 9PPECh. 1.4 - Prob. 10PPECh. 1.4 - Prob. 11PPECh. 1.4 - Prob. 12PPECh. 1.4 - Prob. 13PPECh. 1.4 - Prob. 14PPECh. 1.4 - Prob. 15PPECh. 1.4 - Prob. 16PPECh. 1.4 - Prob. 17PPECh. 1.4 - Prob. 18PPECh. 1.4 - Prob. 19PPECh. 1.4 - Prob. 20PPECh. 1.4 - Prob. 21PPECh. 1.4 - Prob. 22PPECh. 1.4 - Prob. 23PPECh. 1.4 - Prob. 24PPECh. 1.4 - Prob. 25PPECh. 1.4 - Prob. 26PPECh. 1.4 - Prob. 27PPECh. 1.4 - Prob. 28PPECh. 1.4 - Prob. 29PPECh. 1.4 - Prob. 30PPECh. 1.4 - Prob. 31PPECh. 1.4 - Prob. 32PPECh. 1.4 - Prob. 33PPECh. 1.4 - Prob. 34PPECh. 1.4 - Prob. 35PPECh. 1.4 - Prob. 36PPECh. 1.4 - Prob. 37PPECh. 1.4 - Prob. 38PPECh. 1.4 - Prob. 39PPECh. 1.4 - Prob. 40PPECh. 1.4 - Prob. 41PPECh. 1.4 - Prob. 42PPECh. 1.4 - Prob. 43PPECh. 1.4 - Prob. 44PPECh. 1.4 - Prob. 45PPECh. 1.4 - Prob. 46PPECh. 1.4 - Prob. 47PPECh. 1.4 - Prob. 48PPECh. 1.4 - Prob. 49PPECh. 1.4 - Prob. 50PPECh. 1.4 - Prob. 51PPECh. 1.4 - Prob. 52PPECh. 1.4 - Prob. 53PPECh. 1.4 - Prob. 54PPECh. 1.4 - Prob. 55PPECh. 1.4 - Prob. 56PPECh. 1.4 - Prob. 57PPECh. 1.4 - Prob. 58STPCh. 1.4 - Prob. 59STPCh. 1.4 - Prob. 60STPCh. 1.4 - Prob. 61STPCh. 1.4 - Prob. 62RECh. 1.4 - Prob. 63RECh. 1.4 - Prob. 64RECh. 1.4 - Prob. 65RECh. 1.4 - Prob. 66RECh. 1.4 - Prob. 67RECh. 1.4 - Prob. 68RECh. 1.4 - Prob. 1MCQCh. 1.4 - Prob. 2MCQCh. 1.4 - Prob. 3MCQCh. 1.4 - Prob. 4MCQCh. 1.4 - Prob. 5MCQCh. 1.4 - Prob. 6MCQCh. 1.4 - Prob. 7MCQCh. 1.4 - Prob. 8MCQCh. 1.4 - Prob. 9MCQCh. 1.4 - Prob. 10MCQCh. 1.4 - Prob. 11MCQCh. 1.4 - Prob. 12MCQCh. 1.4 - Prob. 13MCQCh. 1.4 - Prob. 14MCQCh. 1.4 - Prob. 15MCQCh. 1.4 - Prob. 16MCQCh. 1.4 - Prob. 17MCQCh. 1.4 - Prob. 18MCQCh. 1.4 - Prob. 19MCQCh. 1.5 - Prob. 1PCh. 1.5 - Prob. 2PCh. 1.5 - Prob. 3PCh. 1.5 - Prob. 4PCh. 1.5 - Prob. 1LCCh. 1.5 - Prob. 2LCCh. 1.5 - Prob. 3LCCh. 1.5 - Prob. 4LCCh. 1.5 - Prob. 5LCCh. 1.5 - Prob. 6LCCh. 1.5 - Prob. 7LCCh. 1.5 - Prob. 8LCCh. 1.5 - Prob. 9LCCh. 1.5 - Prob. 10PPECh. 1.5 - Prob. 11PPECh. 1.5 - Prob. 12PPECh. 1.5 - Prob. 13PPECh. 1.5 - Prob. 14PPECh. 1.5 - Prob. 15PPECh. 1.5 - Prob. 16PPECh. 1.5 - Prob. 17PPECh. 1.5 - Prob. 18PPECh. 1.5 - Prob. 19PPECh. 1.5 - Prob. 20PPECh. 1.5 - Prob. 21PPECh. 1.5 - Prob. 22PPECh. 1.5 - Prob. 23PPECh. 1.5 - Prob. 24PPECh. 1.5 - Prob. 25PPECh. 1.5 - Prob. 26PPECh. 1.5 - Prob. 27PPECh. 1.5 - Prob. 28PPECh. 1.5 - Prob. 29PPECh. 1.5 - Prob. 30PPECh. 1.5 - Prob. 31PPECh. 1.5 - Prob. 32PPECh. 1.5 - Prob. 33PPECh. 1.5 - Prob. 34PPECh. 1.5 - Prob. 35PPECh. 1.5 - Prob. 36PPECh. 1.5 - Prob. 37PPECh. 1.5 - Prob. 38PPECh. 1.5 - Prob. 39PPECh. 1.5 - Prob. 40PPECh. 1.5 - Prob. 41PPECh. 1.5 - Prob. 42PPECh. 1.5 - Prob. 43PPECh. 1.5 - Prob. 44PPECh. 1.5 - Prob. 45PPECh. 1.5 - Prob. 46PPECh. 1.5 - Prob. 47PPECh. 1.5 - Prob. 48PPECh. 1.5 - Prob. 49PPECh. 1.5 - Prob. 50PPECh. 1.5 - Prob. 51PPECh. 1.5 - Prob. 52PPECh. 1.5 - Prob. 53PPECh. 1.5 - Prob. 54PPECh. 1.5 - Prob. 55PPECh. 1.5 - Prob. 56PPECh. 1.5 - Prob. 57PPECh. 1.5 - Prob. 58PPECh. 1.5 - Prob. 59PPECh. 1.5 - Prob. 60PPECh. 1.5 - Prob. 61PPECh. 1.5 - Prob. 62PPECh. 1.5 - Prob. 63PPECh. 1.5 - Prob. 64PPECh. 1.5 - Prob. 65PPECh. 1.5 - Prob. 66PPECh. 1.5 - Prob. 67PPECh. 1.5 - Prob. 68PPECh. 1.5 - Prob. 69PPECh. 1.5 - Prob. 70STPCh. 1.5 - Prob. 71STPCh. 1.5 - Prob. 72STPCh. 1.5 - Prob. 73STPCh. 1.5 - Prob. 74STPCh. 1.5 - Prob. 75MRCh. 1.5 - Prob. 76MRCh. 1.5 - Prob. 77MRCh. 1.5 - Prob. 78MRCh. 1.5 - Prob. 79MRCh. 1.5 - Prob. 80MRCh. 1.5 - Prob. 81MRCh. 1.5 - Prob. 82MRCh. 1.5 - Prob. 83MRCh. 1.5 - Prob. 84MRCh. 1.5 - Prob. 85MRCh. 1.6 - Prob. 1PCh. 1.6 - Prob. 2PCh. 1.6 - Prob. 3PCh. 1.6 - Prob. 4PCh. 1.6 - Prob. 1LCCh. 1.6 - Prob. 2LCCh. 1.6 - Prob. 3LCCh. 1.6 - Prob. 4LCCh. 1.6 - Prob. 5LCCh. 1.6 - Prob. 6LCCh. 1.6 - Prob. 7LCCh. 1.6 - Prob. 8PPECh. 1.6 - Prob. 9PPECh. 1.6 - Prob. 10PPECh. 1.6 - Prob. 11PPECh. 1.6 - Prob. 12PPECh. 1.6 - Prob. 13PPECh. 1.6 - Prob. 14PPECh. 1.6 - Prob. 15PPECh. 1.6 - Prob. 16PPECh. 1.6 - Prob. 17PPECh. 1.6 - Prob. 18PPECh. 1.6 - Prob. 19PPECh. 1.6 - Prob. 20PPECh. 1.6 - Prob. 21PPECh. 1.6 - Prob. 22PPECh. 1.6 - Prob. 23PPECh. 1.6 - Prob. 24PPECh. 1.6 - Prob. 25PPECh. 1.6 - Prob. 26PPECh. 1.6 - Prob. 27PPECh. 1.6 - Prob. 28PPECh. 1.6 - Prob. 29PPECh. 1.6 - Prob. 30PPECh. 1.6 - Prob. 31PPECh. 1.6 - Prob. 32PPECh. 1.6 - Prob. 33PPECh. 1.6 - Prob. 34PPECh. 1.6 - Prob. 35PPECh. 1.6 - Prob. 36PPECh. 1.6 - Prob. 37PPECh. 1.6 - Prob. 38PPECh. 1.6 - Prob. 39PPECh. 1.6 - Prob. 40PPECh. 1.6 - Prob. 41PPECh. 1.6 - Prob. 42PPECh. 1.6 - Prob. 43PPECh. 1.6 - Prob. 44PPECh. 1.6 - Prob. 45PPECh. 1.6 - Prob. 46PPECh. 1.6 - Prob. 47PPECh. 1.6 - Prob. 48PPECh. 1.6 - Prob. 49PPECh. 1.6 - Prob. 50PPECh. 1.6 - Prob. 51PPECh. 1.6 - Prob. 52PPECh. 1.6 - Prob. 53PPECh. 1.6 - Prob. 54PPECh. 1.6 - Prob. 55PPECh. 1.6 - Prob. 56PPECh. 1.6 - Prob. 57PPECh. 1.6 - Prob. 58PPECh. 1.6 - Prob. 59PPECh. 1.6 - Prob. 60PPECh. 1.6 - Prob. 61PPECh. 1.6 - Prob. 62PPECh. 1.6 - Prob. 63PPECh. 1.6 - Prob. 64PPECh. 1.6 - Prob. 65PPECh. 1.6 - Prob. 66PPECh. 1.6 - Prob. 67PPECh. 1.6 - Prob. 68PPECh. 1.6 - Prob. 69PPECh. 1.6 - Prob. 70STPCh. 1.6 - Prob. 71STPCh. 1.6 - Prob. 72STPCh. 1.6 - Prob. 73MRCh. 1.6 - Prob. 74MRCh. 1.6 - Prob. 75MRCh. 1.6 - Prob. 76MRCh. 1.6 - Prob. 77MRCh. 1.6 - Prob. 78MRCh. 1.6 - Prob. 1CBCh. 1.6 - Prob. 2CBCh. 1.6 - Prob. 3CBCh. 1.6 - Prob. 4CBCh. 1.6 - Prob. 5CBCh. 1.6 - Prob. 6CBCh. 1.6 - Prob. 7CBCh. 1.6 - Prob. 8CBCh. 1.6 - Prob. 9CBCh. 1.6 - Prob. 10CBCh. 1.6 - Prob. 11CBCh. 1.6 - Prob. 12CBCh. 1.6 - Prob. 13CBCh. 1.6 - Prob. 14CBCh. 1.6 - Prob. 15CBCh. 1.6 - Prob. 16CBCh. 1.6 - Prob. 17CBCh. 1.6 - Prob. 18CBCh. 1.7 - Prob. 1PCh. 1.7 - Prob. 2PCh. 1.7 - Prob. 3PCh. 1.7 - Prob. 4PCh. 1.7 - Prob. 5PCh. 1.7 - Prob. 1LCCh. 1.7 - Prob. 2LCCh. 1.7 - Prob. 3LCCh. 1.7 - Prob. 4LCCh. 1.7 - Prob. 5LCCh. 1.7 - Prob. 6LCCh. 1.7 - Prob. 7LCCh. 1.7 - Prob. 8LCCh. 1.7 - Prob. 9PPECh. 1.7 - Prob. 10PPECh. 1.7 - Prob. 11PPECh. 1.7 - Prob. 12PPECh. 1.7 - Prob. 13PPECh. 1.7 - Prob. 14PPECh. 1.7 - Prob. 15PPECh. 1.7 - Prob. 16PPECh. 1.7 - Prob. 17PPECh. 1.7 - Prob. 18PPECh. 1.7 - Prob. 19PPECh. 1.7 - Prob. 20PPECh. 1.7 - Prob. 21PPECh. 1.7 - Prob. 22PPECh. 1.7 - Prob. 23PPECh. 1.7 - Prob. 24PPECh. 1.7 - Prob. 25PPECh. 1.7 - Prob. 26PPECh. 1.7 - Prob. 27PPECh. 1.7 - Prob. 28PPECh. 1.7 - Prob. 29PPECh. 1.7 - Prob. 30PPECh. 1.7 - Prob. 31PPECh. 1.7 - Prob. 32PPECh. 1.7 - Prob. 33PPECh. 1.7 - Prob. 34PPECh. 1.7 - Prob. 35PPECh. 1.7 - Prob. 36PPECh. 1.7 - Prob. 37PPECh. 1.7 - Prob. 38PPECh. 1.7 - Prob. 39PPECh. 1.7 - Prob. 40PPECh. 1.7 - Prob. 41PPECh. 1.7 - Prob. 42PPECh. 1.7 - Prob. 43PPECh. 1.7 - Prob. 44PPECh. 1.7 - Prob. 45PPECh. 1.7 - Prob. 46PPECh. 1.7 - Prob. 47PPECh. 1.7 - Prob. 48PPECh. 1.7 - Prob. 49PPECh. 1.7 - Prob. 50PPECh. 1.7 - Prob. 51PPECh. 1.7 - Prob. 52PPECh. 1.7 - Prob. 53PPECh. 1.7 - Prob. 54PPECh. 1.7 - Prob. 55PPECh. 1.7 - Prob. 56PPECh. 1.7 - Prob. 57PPECh. 1.7 - Prob. 58PPECh. 1.7 - Prob. 59PPECh. 1.7 - Prob. 60PPECh. 1.7 - Prob. 61PPECh. 1.7 - Prob. 62PPECh. 1.7 - Prob. 63PPECh. 1.7 - Prob. 64PPECh. 1.7 - Prob. 65PPECh. 1.7 - Prob. 66PPECh. 1.7 - Prob. 67PPECh. 1.7 - Prob. 68PPECh. 1.7 - Prob. 69PPECh. 1.7 - Prob. 70PPECh. 1.7 - Prob. 71PPECh. 1.7 - Prob. 72PPECh. 1.7 - Prob. 73PPECh. 1.7 - Prob. 74PPECh. 1.7 - Prob. 75PPECh. 1.7 - Prob. 76PPECh. 1.7 - Prob. 77PPECh. 1.7 - Prob. 78PPECh. 1.7 - Prob. 79PPECh. 1.7 - Prob. 80PPECh. 1.7 - Prob. 81PPECh. 1.7 - Prob. 82PPECh. 1.7 - Prob. 83PPECh. 1.7 - Prob. 84PPECh. 1.7 - Prob. 85PPECh. 1.7 - Prob. 86PPECh. 1.7 - Prob. 87PPECh. 1.7 - Prob. 88PPECh. 1.7 - Prob. 89PPECh. 1.7 - Prob. 90PPECh. 1.7 - Prob. 1MPCh. 1.8 - Prob. 1PCh. 1.8 - Prob. 2PCh. 1.8 - Prob. 3PCh. 1.8 - Prob. 4PCh. 1.8 - Prob. 5PCh. 1.8 - Prob. 6PCh. 1.8 - Prob. 1LCCh. 1.8 - Prob. 2LCCh. 1.8 - Prob. 3LCCh. 1.8 - Prob. 4LCCh. 1.8 - Prob. 5LCCh. 1.8 - Prob. 6LCCh. 1.8 - Prob. 7PPECh. 1.8 - Prob. 8PPECh. 1.8 - Prob. 9PPECh. 1.8 - Prob. 10PPECh. 1.8 - Prob. 11PPECh. 1.8 - Prob. 12PPECh. 1.8 - Prob. 13PPECh. 1.8 - Prob. 14PPECh. 1.8 - Prob. 15PPECh. 1.8 - Prob. 16PPECh. 1.8 - Prob. 17PPECh. 1.8 - Prob. 18PPECh. 1.8 - Prob. 19PPECh. 1.8 - Prob. 20PPECh. 1.8 - Prob. 21PPECh. 1.8 - Prob. 22PPECh. 1.8 - Prob. 23PPECh. 1.8 - Prob. 24PPECh. 1.8 - Prob. 25PPECh. 1.8 - Prob. 26PPECh. 1.8 - Prob. 27PPECh. 1.8 - Prob. 28PPECh. 1.8 - Prob. 29PPECh. 1.8 - Prob. 30PPECh. 1.8 - Prob. 31PPECh. 1.8 - Prob. 32PPECh. 1.8 - Prob. 33PPECh. 1.8 - Prob. 34PPECh. 1.8 - Prob. 35PPECh. 1.8 - Prob. 36PPECh. 1.8 - Prob. 37PPECh. 1.8 - Prob. 38PPECh. 1.8 - Prob. 39PPECh. 1.8 - Prob. 40PPECh. 1.8 - Prob. 41PPECh. 1.8 - Prob. 42PPECh. 1.8 - Prob. 43PPECh. 1.8 - Prob. 44PPECh. 1.8 - Prob. 45PPECh. 1.8 - Prob. 46PPECh. 1.8 - Prob. 47PPECh. 1.8 - Prob. 48PPECh. 1.8 - Prob. 49PPECh. 1.8 - Prob. 50PPECh. 1.8 - Prob. 51PPECh. 1.8 - Prob. 52PPECh. 1.8 - Prob. 53PPECh. 1.8 - Prob. 54PPECh. 1.8 - Prob. 55PPECh. 1.8 - Prob. 56PPECh. 1.8 - Prob. 57PPECh. 1.8 - Prob. 58PPECh. 1.8 - Prob. 59PPECh. 1.8 - Prob. 60PPECh. 1.8 - Prob. 61PPECh. 1.8 - Prob. 62PPECh. 1.8 - Prob. 63PPECh. 1.8 - Prob. 64PPECh. 1.8 - Prob. 65PPECh. 1.8 - Prob. 66PPECh. 1.8 - Prob. 1MPCh. 1.8 - Prob. 1CBCh. 1.8 - Prob. 2CBCh. 1.9 - Prob. 1RCh. 1.9 - Prob. 2RCh. 1.9 - Prob. 3RCh. 1.9 - Prob. 4RCh. 1.9 - Prob. 1PCh. 1.9 - Prob. 2PCh. 1.9 - Prob. 3PCh. 1.9 - Prob. 1LCCh. 1.9 - Prob. 2LCCh. 1.9 - Prob. 3LCCh. 1.9 - Prob. 4LCCh. 1.9 - Prob. 5LCCh. 1.9 - Prob. 6LCCh. 1.9 - Prob. 7LCCh. 1.9 - Prob. 8PPECh. 1.9 - Prob. 9PPECh. 1.9 - Prob. 10PPECh. 1.9 - Prob. 11PPECh. 1.9 - Prob. 12PPECh. 1.9 - Prob. 13PPECh. 1.9 - Prob. 14PPECh. 1.9 - Prob. 15PPECh. 1.9 - Prob. 16PPECh. 1.9 - Prob. 17PPECh. 1.9 - Prob. 18PPECh. 1.9 - Prob. 19PPECh. 1.9 - Prob. 20PPECh. 1.9 - Prob. 21PPECh. 1.9 - Prob. 22PPECh. 1.9 - Prob. 23PPECh. 1.9 - Prob. 24PPECh. 1.9 - Prob. 25PPECh. 1.9 - Prob. 26PPECh. 1.9 - Prob. 27PPECh. 1.9 - Prob. 28PPECh. 1.9 - Prob. 29PPECh. 1.9 - Prob. 30PPECh. 1.9 - Prob. 31PPECh. 1.9 - Prob. 32PPECh. 1.9 - Prob. 33PPECh. 1.9 - Prob. 34PPECh. 1.9 - Prob. 35PPECh. 1.9 - Prob. 36STPCh. 1.9 - Prob. 37STPCh. 1.9 - Prob. 38STPCh. 1.9 - Prob. 39STPCh. 1.9 - Prob. 40MRCh. 1.9 - Prob. 41MRCh. 1.9 - Prob. 42MRCh. 1.9 - Prob. 43MRCh. 1.9 - Prob. 44MRCh. 1.9 - Prob. 45MRCh. 1.9 - Prob. 46MRCh. 1.9 - Prob. 47MRCh. 1.9 - Prob. 48MRCh. 1.9 - Prob. 49MRCh. 1.9 - Prob. 50MRCh. 1.9 - Prob. 51MRCh. 1.9 - Prob. 52MRCh. 1.9 - Prob. 53MRCh. 1.9 - Prob. 54MRCh. 1 - Prob. 1GRCh. 1 - Prob. 2GRCh. 1 - Prob. 3GRCh. 1 - Prob. 4GRCh. 1 - Prob. 5GRCh. 1 - Prob. 6GRCh. 1 - Prob. 7GRCh. 1 - Prob. 8GRCh. 1 - Prob. 9GRCh. 1 - Prob. 10GRCh. 1 - Prob. 11GRCh. 1 - Prob. 12GRCh. 1 - Prob. 13GRCh. 1 - Prob. 14GRCh. 1 - Prob. 15GRCh. 1 - Prob. 16GRCh. 1 - Prob. 17GRCh. 1 - Prob. 18GRCh. 1 - Prob. 19GRCh. 1 - Prob. 20GRCh. 1 - Prob. 21GRCh. 1 - Prob. 22GRCh. 1 - Prob. 23GRCh. 1 - Prob. 24GRCh. 1 - Prob. 25GRCh. 1 - Prob. 26GRCh. 1 - Prob. 27GRCh. 1 - Prob. 1CRCh. 1 - Prob. 2CRCh. 1 - Prob. 3CRCh. 1 - Prob. 4CRCh. 1 - Prob. 5CRCh. 1 - Prob. 6CRCh. 1 - Prob. 7CRCh. 1 - Prob. 8CRCh. 1 - Prob. 9CRCh. 1 - Prob. 10CRCh. 1 - Prob. 11CRCh. 1 - Prob. 12CRCh. 1 - Prob. 13CRCh. 1 - Prob. 14CRCh. 1 - Prob. 15CRCh. 1 - Prob. 16CRCh. 1 - Prob. 17CRCh. 1 - Prob. 18CRCh. 1 - Prob. 19CRCh. 1 - Prob. 20CRCh. 1 - Prob. 21CRCh. 1 - Prob. 22CRCh. 1 - Prob. 23CRCh. 1 - Prob. 24CRCh. 1 - Prob. 25CRCh. 1 - Prob. 26CRCh. 1 - Prob. 27CRCh. 1 - Prob. 28CRCh. 1 - Prob. 29CRCh. 1 - Prob. 30CRCh. 1 - Prob. 31CRCh. 1 - Prob. 32CRCh. 1 - Prob. 33CRCh. 1 - Prob. 34CRCh. 1 - Prob. 35CRCh. 1 - Prob. 36CRCh. 1 - Prob. 37CRCh. 1 - Prob. 38CRCh. 1 - Prob. 39CRCh. 1 - Prob. 40CRCh. 1 - Prob. 41CRCh. 1 - Prob. 42CRCh. 1 - Prob. 43CRCh. 1 - Prob. 44CRCh. 1 - Prob. 45CRCh. 1 - Prob. 46CRCh. 1 - Prob. 47CRCh. 1 - Prob. 48CRCh. 1 - Prob. 49CRCh. 1 - Prob. 50CRCh. 1 - Prob. 51CRCh. 1 - Prob. 52CRCh. 1 - Prob. 53CRCh. 1 - Prob. 54CRCh. 1 - Prob. 55CRCh. 1 - Prob. 56CRCh. 1 - Prob. 57CRCh. 1 - Prob. 58CRCh. 1 - Prob. 59CRCh. 1 - Prob. 60CRCh. 1 - Prob. 61CRCh. 1 - Prob. 62CRCh. 1 - Prob. 63CRCh. 1 - Prob. 64CRCh. 1 - Prob. 65CRCh. 1 - Prob. 66CRCh. 1 - Prob. 67CRCh. 1 - Prob. 68CRCh. 1 - Prob. 69CRCh. 1 - Prob. 70CRCh. 1 - Prob. 71CRCh. 1 - Prob. 72CRCh. 1 - Prob. 73CRCh. 1 - Prob. 74CRCh. 1 - Prob. 75CRCh. 1 - Prob. 76CRCh. 1 - Prob. 77CRCh. 1 - Prob. 78CRCh. 1 - Prob. 79CRCh. 1 - Prob. 80CRCh. 1 - Prob. 81CRCh. 1 - Prob. 82CRCh. 1 - Prob. 83CRCh. 1 - Prob. 84CRCh. 1 - Prob. 85CRCh. 1 - Prob. 86CRCh. 1 - Prob. 87CRCh. 1 - Prob. 88CRCh. 1 - Prob. 89CRCh. 1 - Prob. 90CRCh. 1 - Prob. 91CRCh. 1 - Prob. 92CRCh. 1 - Prob. 93CRCh. 1 - Prob. 94CRCh. 1 - Prob. 95CRCh. 1 - Prob. 96CRCh. 1 - Prob. 97CRCh. 1 - Prob. 98CRCh. 1 - Prob. 99CRCh. 1 - Prob. 1CTCh. 1 - Prob. 2CTCh. 1 - Prob. 3CTCh. 1 - Prob. 4CTCh. 1 - Prob. 5CTCh. 1 - Prob. 6CTCh. 1 - Prob. 7CTCh. 1 - Prob. 8CTCh. 1 - Prob. 9CTCh. 1 - Prob. 10CTCh. 1 - Prob. 11CTCh. 1 - Prob. 12CTCh. 1 - Prob. 13CTCh. 1 - Prob. 14CTCh. 1 - Prob. 15CTCh. 1 - Prob. 16CTCh. 1 - Prob. 17CTCh. 1 - Prob. 18CTCh. 1 - Prob. 19CTCh. 1 - Prob. 20CTCh. 1 - Prob. 21CTCh. 1 - Prob. 22CTCh. 1 - Prob. 23CTCh. 1 - Prob. 24CTCh. 1 - Prob. 1CCSRCh. 1 - Prob. 2CCSRCh. 1 - Prob. 3CCSRCh. 1 - Prob. 4CCSRCh. 1 - Prob. 5CCSRCh. 1 - Prob. 6CCSRCh. 1 - Prob. 7CCSRCh. 1 - Prob. 8CCSRCh. 1 - Prob. 9CCSRCh. 1 - Prob. 10CCSRCh. 1 - Prob. 11CCSRCh. 1 - Prob. 12CCSRCh. 1 - Prob. 13CCSRCh. 1 - Prob. 14CCSRCh. 1 - Prob. 15CCSRCh. 1 - Prob. 16CCSRCh. 1 - Prob. 17CCSRCh. 1 - Prob. 18CCSRCh. 1 - Prob. 19CCSRCh. 1 - Prob. 20CCSRCh. 1 - Prob. 21CCSRCh. 1 - Prob. 22CCSRCh. 1 - Prob. 23CCSRCh. 1 - Prob. 24CCSR
Additional Math Textbook Solutions
Find more solutions based on key concepts
Sixty percent of the students at a certain school wear neither a ring nor a necklace. Twenty percent wear a rin...
A First Course in Probability (10th Edition)
Hypothesis Testing Using a P-Value In Exercises 31–36,
identify the claim and state H0 and Ha.
find the standar...
Elementary Statistics: Picturing the World (7th Edition)
Trigonometric substitutions Evaluate the following integrals. 31. x29xdx,x3
Calculus: Early Transcendentals (2nd Edition)
Applying the Empirical Rule with z-Scores The Empirical Rule applies rough approximations to probabilities for ...
Introductory Statistics
The four flaws in the given survey.
Elementary Statistics
The following set of data is from sample of n=5: a. Compute the mean, median, and mode. b. Compute the range, v...
Basic Business Statistics, Student Value Edition
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- Într-un bloc sunt apartamente cu 2 camere și apartamente cu 3 camere , în total 20 de apartamente și 45 de camere.Calculați câte apartamente sunt cu 2 camere și câte apartamente sunt cu 3 camere.arrow_forward1.2.19. Let and s be natural numbers. Let G be the simple graph with vertex set Vo... V„−1 such that v; ↔ v; if and only if |ji| Є (r,s). Prove that S has exactly k components, where k is the greatest common divisor of {n, r,s}.arrow_forwardQuestion 3 over a field K. In this question, MË(K) denotes the set of n × n matrices (a) Suppose that A Є Mn(K) is an invertible matrix. Is it always true that A is equivalent to A-¹? Justify your answer. (b) Let B be given by 8 B = 0 7 7 0 -7 7 Working over the field F2 with 2 elements, compute the rank of B as an element of M2(F2). (c) Let 1 C -1 1 [4] [6] and consider C as an element of M3(Q). Determine the minimal polynomial mc(x) and hence, or otherwise, show that C can not be diagonalised. [7] (d) Show that C in (c) considered as an element of M3(R) can be diagonalised. Write down all the eigenvalues. Show your working. [8]arrow_forward
- R denotes the field of real numbers, Q denotes the field of rationals, and Fp denotes the field of p elements given by integers modulo p. You may refer to general results from lectures. Question 1 For each non-negative integer m, let R[x]m denote the vector space consisting of the polynomials in x with coefficients in R and of degree ≤ m. x²+2, V3 = 5. Prove that (V1, V2, V3) is a linearly independent (a) Let vi = x, V2 = list in R[x] 3. (b) Let V1, V2, V3 be as defined in (a). Find a vector v € R[×]3 such that (V1, V2, V3, V4) is a basis of R[x] 3. [8] [6] (c) Prove that the map ƒ from R[x] 2 to R[x]3 given by f(p(x)) = xp(x) — xp(0) is a linear map. [6] (d) Write down the matrix for the map ƒ defined in (c) with respect to the basis (2,2x + 1, x²) of R[x] 2 and the basis (1, x, x², x³) of R[x] 3. [5]arrow_forwardQuestion 4 (a) The following matrices represent linear maps on R² with respect to an orthonormal basis: = [1/√5 2/√5 [2/√5 -1/√5] " [1/√5 2/√5] A = B = [2/√5 1/√5] 1 C = D = = = [ 1/3/5 2/35] 1/√5 2/√5 -2/√5 1/√5' For each of the matrices A, B, C, D, state whether it represents a self-adjoint linear map, an orthogonal linear map, both, or neither. (b) For the quadratic form q(x, y, z) = y² + 2xy +2yz over R, write down a linear change of variables to u, v, w such that q in these terms is in canonical form for Sylvester's Law of Inertia. [6] [4]arrow_forwardpart b pleasearrow_forward
- Question 5 (a) Let a, b, c, d, e, ƒ Є K where K is a field. Suppose that the determinant of the matrix a cl |df equals 3 and the determinant of determinant of the matrix a+3b cl d+3e f ГЪ e [ c ] equals 2. Compute the [5] (b) Calculate the adjugate Adj (A) of the 2 × 2 matrix [1 2 A = over R. (c) Working over the field F3 with 3 elements, use row and column operations to put the matrix [6] 0123] A = 3210 into canonical form for equivalence and write down the canonical form. What is the rank of A as a matrix over F3? 4arrow_forwardQuestion 2 In this question, V = Q4 and - U = {(x, y, z, w) EV | x+y2w+ z = 0}, W = {(x, y, z, w) € V | x − 2y + w − z = 0}, Z = {(x, y, z, w) € V | xyzw = 0}. (a) Determine which of U, W, Z are subspaces of V. Justify your answers. (b) Show that UW is a subspace of V and determine its dimension. (c) Is VU+W? Is V = UW? Justify your answers. [10] [7] '00'arrow_forwardTools Sign in Different masses and Indicated velocities Rotational inert > C C Chegg 39. The balls shown have different masses and speeds. Rank the following from greatest to least: 2.0 m/s 8.5 m/s 9.0 m/s 12.0 m/s 1.0 kg A 1.2 kg B 0.8 kg C 5.0 kg D C a. The momenta b. The impulses needed to stop the balls Solved 39. The balls shown have different masses and speeds. | Chegg.com Images may be subject to copyright. Learn More Share H Save Visit > quizlet.com%2FBoyE3qwOAUqXvw95Fgh5Rw.jpg&imgrefurl=https%3A%2F%2Fquizlet.com%2F529359992%2Fc. Xarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
Algebra and Trigonometry (6th Edition)
Algebra
ISBN:9780134463216
Author:Robert F. Blitzer
Publisher:PEARSON
Contemporary Abstract Algebra
Algebra
ISBN:9781305657960
Author:Joseph Gallian
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Algebra And Trigonometry (11th Edition)
Algebra
ISBN:9780135163078
Author:Michael Sullivan
Publisher:PEARSON
Introduction to Linear Algebra, Fifth Edition
Algebra
ISBN:9780980232776
Author:Gilbert Strang
Publisher:Wellesley-Cambridge Press
College Algebra (Collegiate Math)
Algebra
ISBN:9780077836344
Author:Julie Miller, Donna Gerken
Publisher:McGraw-Hill Education
2.1 Introduction to inequalities; Author: Oli Notes;https://www.youtube.com/watch?v=D6erN5YTlXE;License: Standard YouTube License, CC-BY
GCSE Maths - What are Inequalities? (Inequalities Part 1) #56; Author: Cognito;https://www.youtube.com/watch?v=e_tY6X5PwWw;License: Standard YouTube License, CC-BY
Introduction to Inequalities | Inequality Symbols | Testing Solutions for Inequalities; Author: Scam Squad Math;https://www.youtube.com/watch?v=paZSN7sV1R8;License: Standard YouTube License, CC-BY