
Concept explainers
a
To make a table showing the relation between body and water weight for people weighing 100, 105, 110,120,125 and 130 pounds.
a
Explanation of Solution
Given:
The given relation is
Where w = weight of water in pounds.
b = body weight in pounds.
Calculation:
When the body weight ( b) =100 pounds, weight of water ( w ) is =
Similarly,
| Values of ‘ b’ | Values of ‘ w’ |
| 100 | |
| 105 | |
| 110 | |
| 120 | |
| 125 | |
| 130 |
Conclusion:
The above table shows the relation between body and water weight for people.
b
To identify the dependent and independent variables from the given relation.
b
Answer to Problem 6CB
Weight of body is independent variable.
Weight of water is dependent variable.
Explanation of Solution
Given:
The given relation is
Independent variables are those variables which keeps on changing and they are unaffected by the change of any other parameter. For example: - Time.
Hence, Weight of the body ( b) is the deciding parameter which does not depend on other variable. So it is the independent variable.
Weight of the water ( w) depends on weight of the body ( b) as per the given relation.
So, the Weight of the water is the dependent variable.
Conclusion:
Therefore, weight of body is independent variable and weight of water is dependent variable.
c
To write: the domain and range of the relation
c
Answer to Problem 6CB
Domain
Range
Explanation of Solution
Given:
The relation is
Domain is all the values of x - axis that is defined in the given relation.
Range is all the values of y - axis that are possible for corresponding values of x - axis.
Hence, for the relation
Calculation for graph:
Consider
| Values of ‘ b’ | Values of ‘ w’ |
| 100 | |
| 105 | |
| 110 | |
| 120 | |
| 125 | |
| 130 |
By taking different values of b , the graph can be plotted.
Graph:
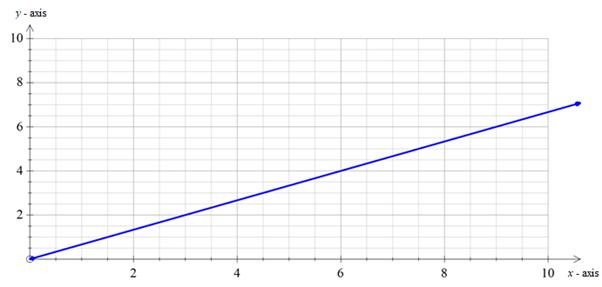
Interpretation:
From the above graph, it is clear that,
As the weight of the body increases, the weight of the water also increases.
d
To reverse the independent and dependent variable of the given relation, graph it and interpret the meaning of the graph.
d
Explanation of Solution
Given:
The relation is
Here, Weight of the body ( b ) is the independent variable.
Weight of water ( w) is the dependent variable
The given relation after reversing the independent and dependent variable is
This means, for every 3 pounds of water, there will be 2 pounds of body weight for an adult.
Calculation for graph:
Consider
| Values of ‘ w’ | Values of ‘ b’ |
| 100 | |
| 105 | |
| 110 | |
| 120 | |
| 125 | |
| 130 |
Graph:
 In the above graph, x - axis denotes the weight of the water ( w) in pounds.
In the above graph, x - axis denotes the weight of the water ( w) in pounds.
y - axis denotes the weight of the body ( b ) in pounds.
Interpretation:
From the above graph, it is clear that,
As the weight of the water increases, the weight of the body also increases.
Chapter 1 Solutions
High School Math 2015 Common Core Algebra 1 Student Edition Grade 8/9
Additional Math Textbook Solutions
Introductory Statistics
Thinking Mathematically (6th Edition)
A Problem Solving Approach To Mathematics For Elementary School Teachers (13th Edition)
Calculus: Early Transcendentals (2nd Edition)
Elementary Statistics (13th Edition)
A First Course in Probability (10th Edition)
- Can you check if my step is correct?arrow_forwardI need help explaining on this example on how can I define the Time-Domain Function, Apply the Laplace Transformation Formula, and Simplify to Find the Frequency-Domain Expression. I need to understand on finding Y(s)arrow_forwardI need help explaining on this example on how can I define the Time-Domain Function, Apply the Laplace Transformation Formula, andarrow_forward
- ma Classes Term. Spring 2025 Title Details Credit Hours CRN Schedule Type Grade Mode Level Date Status Message *MATHEMATICS FOR MANAGEME... MTH 245, 400 4 54835 Online Normal Grading Mode Ecampus Undergradu... 03/21/2025 Registered **Web Registered... *SOIL SCIENCE CSS 205, 400 0 52298 Online Normal Grading Mode Undergraduate 03/21/2025 Waitlisted Waitlist03/21/2025 PLANT PATHOLOGY BOT 451, 400 4 56960 Online Normal Grading Mode Undergraduate 03/21/2025 Registered **Web Registered... Records: 3 Schedule Schedule Detailsarrow_forwardHere is an augmented matrix for a system of equations (three equations and three variables). Let the variables used be x, y, and z: 1 2 4 6 0 1 -1 3 0 0 1 4 Note: that this matrix is already in row echelon form. Your goal is to use this row echelon form to revert back to the equations that this represents, and then to ultimately solve the system of equations by finding x, y and z. Input your answer as a coordinate point: (x,y,z) with no spaces.arrow_forward1 3 -4 In the following matrix perform the operation 2R1 + R2 → R2. -2 -1 6 After you have completed this, what numeric value is in the a22 position?arrow_forward
- 5 -2 0 1 6 12 Let A = 6 7 -1 and B = 1/2 3 -14 -2 0 4 4 4 0 Compute -3A+2B and call the resulting matrix R. If rij represent the individual entries in the matrix R, what numeric value is in 131? Input your answer as a numeric value only.arrow_forward1 -2 4 10 My goal is to put the matrix 5 -1 1 0 into row echelon form using Gaussian elimination. 3 -2 6 9 My next step is to manipulate this matrix using elementary row operations to get a 0 in the a21 position. Which of the following operations would be the appropriate elementary row operation to use to get a 0 in the a21 position? O (1/5)*R2 --> R2 ○ 2R1 + R2 --> R2 ○ 5R1+ R2 --> R2 O-5R1 + R2 --> R2arrow_forwardThe 2x2 linear system of equations -2x+4y = 8 and 4x-3y = 9 was put into the following -2 4 8 augmented matrix: 4 -3 9 This augmented matrix is then converted to row echelon form. Which of the following matrices is the appropriate row echelon form for the given augmented matrix? 0 Option 1: 1 11 -2 Option 2: 4 -3 9 Option 3: 10 ܂ -2 -4 5 25 1 -2 -4 Option 4: 0 1 5 1 -2 Option 5: 0 0 20 -4 5 ○ Option 1 is the appropriate row echelon form. ○ Option 2 is the appropriate row echelon form. ○ Option 3 is the appropriate row echelon form. ○ Option 4 is the appropriate row echelon form. ○ Option 5 is the appropriate row echelon form.arrow_forward
- Let matrix A have order (dimension) 2x4 and let matrix B have order (dimension) 4x4. What results when you compute A+B? The resulting matrix will have dimensions of 2x4. ○ The resulting matrix will be a single number (scalar). The resulting matrix will have dimensions of 4x4. A+B is undefined since matrix A and B do not have the same dimensions.arrow_forwardIf -1 "[a446]-[254] 4b = -1 , find the values of a and b. ○ There is no solution for a and b. ○ There are infinite solutions for a and b. O a=3, b=3 O a=1, b=2 O a=2, b=1 O a=2, b=2arrow_forwardA student puts a 3x3 system of linear equations is into an augmented matrix. The student then correctly puts the augmented matrix into row echelon form (REF), which yields the following resultant matrix: -2 3 -0.5 10 0 0 0 -2 0 1 -4 Which of the following conclusions is mathematically supported by the work shown about system of linear equations? The 3x3 system of linear equations has no solution. ○ The 3x3 system of linear equations has infinite solutions. The 3x3 system of linear equations has one unique solution.arrow_forward
 Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON
Algebra and Trigonometry (6th Edition)AlgebraISBN:9780134463216Author:Robert F. BlitzerPublisher:PEARSON Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning
Contemporary Abstract AlgebraAlgebraISBN:9781305657960Author:Joseph GallianPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON
Algebra And Trigonometry (11th Edition)AlgebraISBN:9780135163078Author:Michael SullivanPublisher:PEARSON Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press
Introduction to Linear Algebra, Fifth EditionAlgebraISBN:9780980232776Author:Gilbert StrangPublisher:Wellesley-Cambridge Press College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education
College Algebra (Collegiate Math)AlgebraISBN:9780077836344Author:Julie Miller, Donna GerkenPublisher:McGraw-Hill Education





