EBK PRECALCULUS:GRAPHICAL,...-NASTA ED.
10th Edition
ISBN: 9780135795910
Author: Demana
Publisher: PEARSON CO
expand_more
expand_more
format_list_bulleted
Videos
Expert Solution & Answer
Chapter 1.7, Problem 49E
Solution
a.
To find: The function
The function that models the cost of producing
Given information:
The cost of making each unstrung racket is $23 and total of $125000 in fixed overhead costs.
Calculation:
Multiply the number of rackets with the price of each unstrung racket and add fixed overhead costs to get the function that models the cost of producing unstrung rackets as follows:
Conclusion:
The function that models the cost of producing
b.
To find: The function
The function that models the cost of producing
Given information:
The cost of making each unstrung racket is $23 and total of $125000 in fixed overhead costs.
Calculation:
Multiply the number of rackets with the price of each strung racket and add fixed overhead costs to get the function that models the cost of producing unstrung rackets as follows:
Conclusion:
The function that models the cost of producing
c.
To find: The function
The function modelling the revenue generated by selling
Given information:
The cost of making each unstrung racket is $23 and total of $125000 in fixed overhead costs.
The price of an unstrung racket is $56 and the price of a strung racket is $79.
Calculation:
The selling price of one unstrung racket is $56. So, the selling price of
Therefore, the function modelling the revenue generated by selling
Conclusion:
The revenue function is
d.
To find: The function
The function modelling the revenue generated by selling
Given information:
The cost of making each unstrung racket is $23 and total of $125000 in fixed overhead costs.
The price of an unstrung racket is $56 and the price of a strung racket is $79.
Calculation:
The selling price of one unstrung racket is $79. So, the selling price of
Therefore, the function modelling the revenue generated by selling
Conclusion:
The revenue function is
e.
To graph: The functions
Given information:
The cost of making each unstrung racket is $23 and total of $125000 in fixed overhead costs.
The price of an unstrung racket is $56 and the price of a strung racket is $79.
Graph:
Use a graphing tool to draw the graph of the functions as shown below.
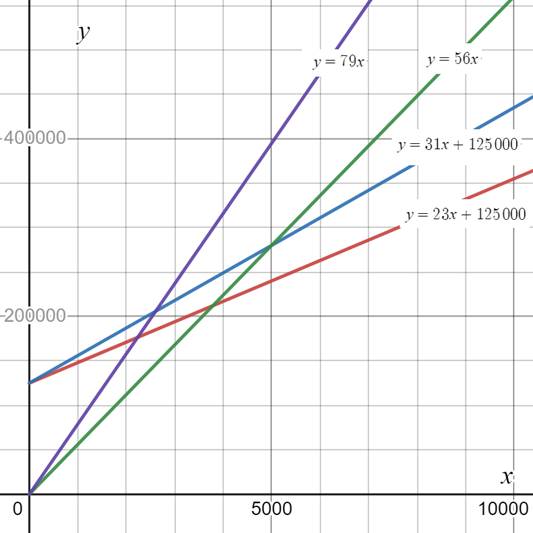
Interpretation:
Selling strung rackets generates more revenue than selling unstrung rackets.
f.
To write: whether the company should manufacture unstrung or strung rackets.
The company should manufacture strung rackets.
Given information:
The cost of making each unstrung racket is $23 and total of $125000 in fixed overhead costs.
The price of an unstrung racket is $56 and the price of a strung racket is $79.
Calculation:
Consider the graph drawn in part (e).
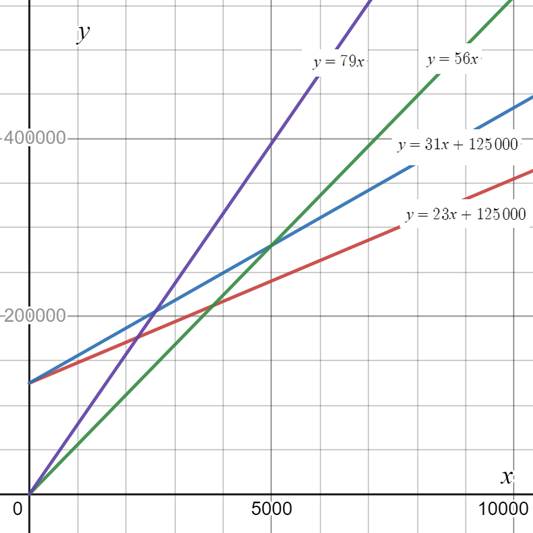
From the graph it can be observed that the revenue generated by selling strung rackets is more than revenue generated by unstrung rackets. Thus, it is recommended to manufacture strung rackets.
Conclusion:
Selling strung rackets generates more revenue than selling unstrung rackets.
Chapter 1 Solutions
EBK PRECALCULUS:GRAPHICAL,...-NASTA ED.
Ch. 1.1 - Prob. 1QRCh. 1.1 - Prob. 2QRCh. 1.1 - Prob. 3QRCh. 1.1 - Prob. 4QRCh. 1.1 - Prob. 5QRCh. 1.1 - Prob. 6QRCh. 1.1 - Prob. 7QRCh. 1.1 - Prob. 8QRCh. 1.1 - Prob. 9QRCh. 1.1 - Prob. 10QR
Ch. 1.1 - Prob. 1ECh. 1.1 - Prob. 2ECh. 1.1 - Prob. 3ECh. 1.1 - Prob. 4ECh. 1.1 - Prob. 5ECh. 1.1 - Prob. 6ECh. 1.1 - Prob. 7ECh. 1.1 - Prob. 8ECh. 1.1 - Prob. 9ECh. 1.1 - Prob. 10ECh. 1.1 - Prob. 11ECh. 1.1 - Prob. 12ECh. 1.1 - Prob. 13ECh. 1.1 - Prob. 14ECh. 1.1 - Prob. 15ECh. 1.1 - Prob. 16ECh. 1.1 - Prob. 18ECh. 1.1 - Prob. 19ECh. 1.1 - Prob. 20ECh. 1.1 - Prob. 21ECh. 1.1 - Prob. 22ECh. 1.1 - Prob. 23ECh. 1.1 - Prob. 24ECh. 1.1 - Prob. 25ECh. 1.1 - Prob. 26ECh. 1.1 - Prob. 27ECh. 1.1 - Prob. 28ECh. 1.1 - Prob. 29ECh. 1.1 - Prob. 30ECh. 1.1 - Prob. 31ECh. 1.1 - Prob. 32ECh. 1.1 - Prob. 33ECh. 1.1 - Prob. 34ECh. 1.1 - Prob. 35ECh. 1.1 - Prob. 36ECh. 1.1 - Prob. 37ECh. 1.1 - Prob. 38ECh. 1.1 - Prob. 39ECh. 1.1 - Prob. 40ECh. 1.1 - Prob. 41ECh. 1.1 - Prob. 42ECh. 1.1 - Prob. 43ECh. 1.1 - Prob. 44ECh. 1.1 - Prob. 45ECh. 1.1 - Prob. 46ECh. 1.1 - Prob. 47ECh. 1.1 - Prob. 48ECh. 1.1 - Prob. 49ECh. 1.1 - Prob. 50ECh. 1.1 - Prob. 51ECh. 1.1 - Prob. 52ECh. 1.1 - Prob. 53ECh. 1.1 - Prob. 54ECh. 1.1 - Prob. 55ECh. 1.1 - Prob. 56ECh. 1.1 - Prob. 57ECh. 1.1 - Prob. 58ECh. 1.1 - Prob. 59ECh. 1.1 - Prob. 60ECh. 1.1 - Prob. 61ECh. 1.1 - Prob. 62ECh. 1.1 - Prob. 63ECh. 1.2 - Prob. 1QRCh. 1.2 - Prob. 2QRCh. 1.2 - Prob. 3QRCh. 1.2 - Prob. 4QRCh. 1.2 - Prob. 5QRCh. 1.2 - Prob. 6QRCh. 1.2 - Prob. 7QRCh. 1.2 - Prob. 8QRCh. 1.2 - Prob. 9QRCh. 1.2 - Prob. 10QRCh. 1.2 - Prob. 1ECh. 1.2 - Prob. 2ECh. 1.2 - Prob. 3ECh. 1.2 - Prob. 4ECh. 1.2 - Prob. 5ECh. 1.2 - Prob. 6ECh. 1.2 - Prob. 7ECh. 1.2 - Prob. 8ECh. 1.2 - Prob. 9ECh. 1.2 - Prob. 10ECh. 1.2 - Prob. 11ECh. 1.2 - Prob. 12ECh. 1.2 - Prob. 13ECh. 1.2 - Prob. 14ECh. 1.2 - Prob. 15ECh. 1.2 - Prob. 16ECh. 1.2 - Prob. 17ECh. 1.2 - Prob. 18ECh. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Prob. 21ECh. 1.2 - Prob. 22ECh. 1.2 - Prob. 23ECh. 1.2 - Prob. 24ECh. 1.2 - Prob. 25ECh. 1.2 - Prob. 26ECh. 1.2 - Prob. 27ECh. 1.2 - Prob. 28ECh. 1.2 - Prob. 29ECh. 1.2 - Prob. 30ECh. 1.2 - Prob. 31ECh. 1.2 - Prob. 32ECh. 1.2 - Prob. 33ECh. 1.2 - Prob. 34ECh. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - Prob. 39ECh. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - Prob. 42ECh. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - Prob. 45ECh. 1.2 - Prob. 46ECh. 1.2 - Prob. 47ECh. 1.2 - Prob. 48ECh. 1.2 - Prob. 49ECh. 1.2 - Prob. 50ECh. 1.2 - Prob. 51ECh. 1.2 - Prob. 52ECh. 1.2 - Prob. 53ECh. 1.2 - Prob. 54ECh. 1.2 - Prob. 55ECh. 1.2 - Prob. 56ECh. 1.2 - Prob. 57ECh. 1.2 - Prob. 58ECh. 1.2 - Prob. 59ECh. 1.2 - Prob. 60ECh. 1.2 - Prob. 61ECh. 1.2 - Prob. 62ECh. 1.2 - Prob. 63ECh. 1.2 - Prob. 64ECh. 1.2 - Prob. 65ECh. 1.2 - Prob. 66ECh. 1.2 - Prob. 67ECh. 1.2 - Prob. 68ECh. 1.2 - Prob. 69ECh. 1.2 - Prob. 70ECh. 1.2 - Prob. 71ECh. 1.2 - Prob. 72ECh. 1.2 - Prob. 73ECh. 1.2 - Prob. 74ECh. 1.2 - Prob. 75ECh. 1.2 - Prob. 76ECh. 1.2 - Prob. 77ECh. 1.2 - Prob. 78ECh. 1.2 - Prob. 79ECh. 1.2 - Prob. 80ECh. 1.2 - Prob. 81ECh. 1.2 - Prob. 82ECh. 1.2 - Prob. 83ECh. 1.2 - Prob. 84ECh. 1.2 - Prob. 85ECh. 1.2 - Prob. 86ECh. 1.2 - Prob. 87ECh. 1.3 - Prob. 1QRCh. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 4QRCh. 1.3 - In Exercises 110, evaluate the expression without...Ch. 1.3 - Prob. 6QRCh. 1.3 - Prob. 7QRCh. 1.3 - Prob. 8QRCh. 1.3 - Prob. 9QRCh. 1.3 - Prob. 10QRCh. 1.3 - Prob. 1ECh. 1.3 - Prob. 2ECh. 1.3 - In Exercises 112, each graph is a slight variation...Ch. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - Prob. 6ECh. 1.3 - Prob. 7ECh. 1.3 - Prob. 8ECh. 1.3 - Prob. 9ECh. 1.3 - Prob. 10ECh. 1.3 - Prob. 11ECh. 1.3 - Prob. 12ECh. 1.3 - Prob. 13ECh. 1.3 - Prob. 14ECh. 1.3 - Prob. 15ECh. 1.3 - Prob. 16ECh. 1.3 - Prob. 17ECh. 1.3 - Prob. 18ECh. 1.3 - Prob. 19ECh. 1.3 - Prob. 20ECh. 1.3 - Prob. 21ECh. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - Prob. 25ECh. 1.3 - Prob. 26ECh. 1.3 - Prob. 27ECh. 1.3 - Prob. 28ECh. 1.3 - Prob. 29ECh. 1.3 - Prob. 30ECh. 1.3 - Prob. 31ECh. 1.3 - Prob. 32ECh. 1.3 - Prob. 33ECh. 1.3 - Prob. 34ECh. 1.3 - Prob. 35ECh. 1.3 - Prob. 36ECh. 1.3 - Prob. 37ECh. 1.3 - Prob. 38ECh. 1.3 - Prob. 39ECh. 1.3 - Prob. 40ECh. 1.3 - Prob. 41ECh. 1.3 - Prob. 42ECh. 1.3 - Prob. 43ECh. 1.3 - Prob. 44ECh. 1.3 - Prob. 45ECh. 1.3 - Prob. 46ECh. 1.3 - Prob. 47ECh. 1.3 - Prob. 48ECh. 1.3 - Prob. 49ECh. 1.3 - Prob. 50ECh. 1.3 - Prob. 51ECh. 1.3 - Prob. 52ECh. 1.3 - Prob. 53ECh. 1.3 - Prob. 54ECh. 1.3 - Prob. 55ECh. 1.3 - Prob. 56ECh. 1.3 - Prob. 57ECh. 1.3 - Prob. 58ECh. 1.3 - Prob. 59ECh. 1.3 - Prob. 60ECh. 1.3 - Prob. 61ECh. 1.3 - Prob. 62ECh. 1.3 - Prob. 63ECh. 1.3 - Prob. 64ECh. 1.3 - Prob. 65ECh. 1.3 - Prob. 67ECh. 1.3 - Prob. 68ECh. 1.3 - Prob. 69ECh. 1.4 - Prob. 1QRCh. 1.4 - Prob. 2QRCh. 1.4 - Prob. 3QRCh. 1.4 - Prob. 4QRCh. 1.4 - Prob. 5QRCh. 1.4 - Prob. 6QRCh. 1.4 - Prob. 7QRCh. 1.4 - Prob. 8QRCh. 1.4 - Prob. 9QRCh. 1.4 - Prob. 10QRCh. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - In Exercises 14 find formulas for the functions...Ch. 1.4 - Prob. 3ECh. 1.4 - Prob. 4ECh. 1.4 - Prob. 5ECh. 1.4 - Prob. 6ECh. 1.4 - Prob. 7ECh. 1.4 - Prob. 8ECh. 1.4 - Prob. 9ECh. 1.4 - Prob. 10ECh. 1.4 - Prob. 11ECh. 1.4 - Prob. 12ECh. 1.4 - Prob. 13ECh. 1.4 - Prob. 14ECh. 1.4 - Prob. 15ECh. 1.4 - Prob. 16ECh. 1.4 - Prob. 17ECh. 1.4 - Prob. 18ECh. 1.4 - Prob. 19ECh. 1.4 - Prob. 20ECh. 1.4 - Prob. 21ECh. 1.4 - Prob. 22ECh. 1.4 - Prob. 23ECh. 1.4 - Prob. 24ECh. 1.4 - Prob. 25ECh. 1.4 - Prob. 26ECh. 1.4 - Prob. 27ECh. 1.4 - Prob. 28ECh. 1.4 - Prob. 29ECh. 1.4 - Prob. 30ECh. 1.4 - Prob. 31ECh. 1.4 - Prob. 32ECh. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - Prob. 35ECh. 1.4 - Prob. 36ECh. 1.4 - Prob. 37ECh. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - Prob. 42ECh. 1.4 - Prob. 43ECh. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - Prob. 46ECh. 1.4 - Prob. 47ECh. 1.4 - Prob. 48ECh. 1.4 - Prob. 49ECh. 1.4 - Prob. 50ECh. 1.4 - Prob. 51ECh. 1.4 - Prob. 52ECh. 1.4 - Prob. 53ECh. 1.4 - Prob. 54ECh. 1.4 - Prob. 55ECh. 1.5 - Prob. 1QRCh. 1.5 - Prob. 2QRCh. 1.5 - Prob. 3QRCh. 1.5 - Prob. 4QRCh. 1.5 - Prob. 5QRCh. 1.5 - Prob. 6QRCh. 1.5 - Prob. 7QRCh. 1.5 - Prob. 8QRCh. 1.5 - Prob. 9QRCh. 1.5 - Prob. 10QRCh. 1.5 - Prob. 1ECh. 1.5 - Prob. 2ECh. 1.5 - Prob. 3ECh. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - Prob. 6ECh. 1.5 - Prob. 7ECh. 1.5 - Prob. 8ECh. 1.5 - Prob. 9ECh. 1.5 - Prob. 10ECh. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - In Exercises 1322, find a formula for f1x . Give...Ch. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - Prob. 17ECh. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - Prob. 21ECh. 1.5 - Prob. 22ECh. 1.5 - Prob. 23ECh. 1.5 - Prob. 24ECh. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - Prob. 28ECh. 1.5 - Prob. 29ECh. 1.5 - Prob. 30ECh. 1.5 - Prob. 31ECh. 1.5 - Prob. 32ECh. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - Prob. 36ECh. 1.5 - Prob. 37ECh. 1.5 - Prob. 38ECh. 1.5 - Prob. 39ECh. 1.5 - Prob. 40ECh. 1.5 - Prob. 41ECh. 1.5 - Prob. 42ECh. 1.5 - Prob. 43ECh. 1.5 - Prob. 44ECh. 1.5 - Prob. 45ECh. 1.5 - Prob. 46ECh. 1.5 - Prob. 47ECh. 1.5 - Prob. 48ECh. 1.5 - Prob. 49ECh. 1.5 - Prob. 50ECh. 1.5 - Prob. 51ECh. 1.6 - Prob. 1QRCh. 1.6 - Prob. 2QRCh. 1.6 - Prob. 3QRCh. 1.6 - Prob. 4QRCh. 1.6 - Prob. 5QRCh. 1.6 - Prob. 6QRCh. 1.6 - Prob. 7QRCh. 1.6 - Prob. 8QRCh. 1.6 - Prob. 9QRCh. 1.6 - Prob. 10QRCh. 1.6 - Prob. 1ECh. 1.6 - Prob. 2ECh. 1.6 - Prob. 3ECh. 1.6 - Prob. 4ECh. 1.6 - Prob. 5ECh. 1.6 - Prob. 6ECh. 1.6 - Prob. 7ECh. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - Prob. 11ECh. 1.6 - Prob. 12ECh. 1.6 - Prob. 13ECh. 1.6 - Prob. 14ECh. 1.6 - Prob. 15ECh. 1.6 - Prob. 16ECh. 1.6 - Prob. 17ECh. 1.6 - Prob. 18ECh. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prob. 23ECh. 1.6 - Prob. 24ECh. 1.6 - Prob. 25ECh. 1.6 - Prob. 26ECh. 1.6 - Prob. 27ECh. 1.6 - Prob. 28ECh. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.6 - Prob. 31ECh. 1.6 - Prob. 32ECh. 1.6 - Prob. 33ECh. 1.6 - Prob. 34ECh. 1.6 - Prob. 35ECh. 1.6 - Prob. 36ECh. 1.6 - Prob. 37ECh. 1.6 - Prob. 38ECh. 1.6 - Prob. 39ECh. 1.6 - Prob. 40ECh. 1.6 - Prob. 41ECh. 1.6 - Prob. 42ECh. 1.6 - Prob. 43ECh. 1.6 - Prob. 44ECh. 1.6 - Prob. 45ECh. 1.6 - Prob. 46ECh. 1.6 - Prob. 47ECh. 1.6 - Prob. 48ECh. 1.6 - Prob. 49ECh. 1.6 - Prob. 50ECh. 1.6 - Prob. 51ECh. 1.6 - Prob. 52ECh. 1.6 - Prob. 53ECh. 1.6 - Prob. 54ECh. 1.6 - Prob. 55ECh. 1.6 - Prob. 56ECh. 1.6 - Prob. 57ECh. 1.6 - Prob. 58ECh. 1.6 - Prob. 59ECh. 1.6 - Prob. 60ECh. 1.6 - Prob. 61ECh. 1.6 - Prob. 62ECh. 1.6 - Prob. 63ECh. 1.6 - Prob. 64ECh. 1.6 - Prob. 65ECh. 1.6 - Prob. 66ECh. 1.6 - Prob. 67ECh. 1.6 - Prob. 68ECh. 1.7 - Prob. 1QRCh. 1.7 - Prob. 2QRCh. 1.7 - Prob. 3QRCh. 1.7 - Prob. 4QRCh. 1.7 - Prob. 5QRCh. 1.7 - Prob. 6QRCh. 1.7 - Prob. 7QRCh. 1.7 - Prob. 8QRCh. 1.7 - Prob. 9QRCh. 1.7 - Prob. 10QRCh. 1.7 - Prob. 1ECh. 1.7 - Prob. 2ECh. 1.7 - Prob. 3ECh. 1.7 - Prob. 4ECh. 1.7 - Prob. 5ECh. 1.7 - Prob. 6ECh. 1.7 - Prob. 7ECh. 1.7 - Prob. 8ECh. 1.7 - In Exercises 110, write a mathematical expression...Ch. 1.7 - Prob. 10ECh. 1.7 - Prob. 11ECh. 1.7 - Prob. 12ECh. 1.7 - Prob. 13ECh. 1.7 - In Exercises 1114, choose a variable and write a...Ch. 1.7 - Prob. 15ECh. 1.7 - In Exercises 1520, write the specified quantity as...Ch. 1.7 - Prob. 17ECh. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - Prob. 25ECh. 1.7 - Prob. 26ECh. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - Prob. 29ECh. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - Prob. 33ECh. 1.7 - Prob. 34ECh. 1.7 - Prob. 35ECh. 1.7 - In Exercises 2136, write an equation for the...Ch. 1.7 - Finding the Model and Solving Water is stored in a...Ch. 1.7 - Prob. 38ECh. 1.7 - Prob. 39ECh. 1.7 - Prob. 40ECh. 1.7 - Prob. 41ECh. 1.7 - Prob. 42ECh. 1.7 - Prob. 43ECh. 1.7 - Prob. 44ECh. 1.7 - Prob. 45ECh. 1.7 - Prob. 46ECh. 1.7 - Prob. 47ECh. 1.7 - Prob. 48ECh. 1.7 - Prob. 49ECh. 1.7 - Prob. 50ECh. 1.7 - Prob. 51ECh. 1 - Prob. 1RECh. 1 - Prob. 2RECh. 1 - Prob. 3RECh. 1 - Prob. 4RECh. 1 - Prob. 5RECh. 1 - Prob. 6RECh. 1 - Prob. 7RECh. 1 - Prob. 8RECh. 1 - Prob. 9RECh. 1 - Prob. 10RECh. 1 - Prob. 11RECh. 1 - Prob. 12RECh. 1 - Prob. 13RECh. 1 - Prob. 14RECh. 1 - Prob. 15RECh. 1 - Prob. 16RECh. 1 - Prob. 17RECh. 1 - Prob. 18RECh. 1 - Prob. 19RECh. 1 - Prob. 20RECh. 1 - Prob. 21RECh. 1 - Prob. 22RECh. 1 - Prob. 23RECh. 1 - Prob. 24RECh. 1 - Prob. 25RECh. 1 - Prob. 26RECh. 1 - Prob. 27RECh. 1 - Prob. 28RECh. 1 - Prob. 29RECh. 1 - Prob. 30RECh. 1 - Prob. 31RECh. 1 - Prob. 32RECh. 1 - Prob. 33RECh. 1 - Prob. 34RECh. 1 - Prob. 35RECh. 1 - Prob. 36RECh. 1 - Prob. 37RECh. 1 - Prob. 38RECh. 1 - Prob. 39RECh. 1 - Prob. 40RECh. 1 - Prob. 41RECh. 1 - Prob. 42RECh. 1 - Prob. 43RECh. 1 - Prob. 44RECh. 1 - Prob. 45RECh. 1 - Prob. 46RECh. 1 - Prob. 47RECh. 1 - Prob. 48RECh. 1 - Prob. 49RECh. 1 - Prob. 50RECh. 1 - Prob. 51RECh. 1 - Prob. 52RECh. 1 - Prob. 53RECh. 1 - Prob. 54RECh. 1 - Prob. 55RECh. 1 - Prob. 56RECh. 1 - Prob. 57RECh. 1 - Prob. 58RECh. 1 - Prob. 59RECh. 1 - Prob. 60RECh. 1 - In Exercises 5964, write the specified quantity as...Ch. 1 - Prob. 62RECh. 1 - Prob. 63RECh. 1 - Prob. 64RECh. 1 - Prob. 65RECh. 1 - Prob. 67RECh. 1 - Prob. 68RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- This question is a previous exam question. I am using it for practice but am stuckarrow_forwardin Q. A firm price of 501: If the Total cast is given by perfect competition sells its products at the TTC = 3Q² +2Q+5. level of output will will be the level of profit at What What Devive the Consumer Curve approach. demand the function maximize this firm's, that using putput level. the indifference prpfit. Q₂. The Total Cost equation in the production of bacon has hypothetical factor a 2 A C= "TC 1000+ 159" +03 ; Where ç. Kash, Bacao - metric bone Compute and 11" tonnes the and average cost at output level of 10. Stretch theme marginal cost of the the shope Carve an the production average, Cost arve 12 tonnes and explain, the relationship between Marginal Cost product es tamen op d Galaxy A71 01 Curve inarrow_forwardif w(x, y, z) = sin' ( xyz) (y zî + x z j + xy k) Find grad (div) at (0.5, 1, 0.5) (xyz)2arrow_forward
- Q2/ verify that grad (hgrad f- f grad h) 1 E = 11 h h₂ where and h are scalar factions.arrow_forward(b) Find the value of each of these sums. Στο 3 • 21 =0 (i) (ii) Σ=1 Σ=023 2arrow_forward(b) For each of the following sets, 6 is an element of that set. (i) {x ER|x is an integer greater than 1} (ii) {x ЄR|x is the cube of an integer} (iii) {6, {6}} (iv) {{6},{6, {6}}} (v) {{{2}}}arrow_forward
- Question 1 Reverse the order of integration to calculate .8 .2 A = = So² Son y1/3 cos² (x²) dx dy. Then the value of sin(A) is -0.952 0.894 0.914 0.811 0.154 -0.134 -0.583 O 0.686 1 ptsarrow_forward3 Calculate the integral approximations T and M6 for 2 x dx. Your answers must be accurate to 8 decimal places. T6= e to search M6- Submit answer Next item Answers Answer # m 0 T F4 F5 The Weather Channel UP DELL F6 F7 % 5 olo in 0 W E R T A S D F G ZX C F8 Score & 7 H FO F10 8 の K B N Marrow_forwardStart with a circle of radius r=9. Form the two shaded regions pictured below. Let f(6) be the area of the shaded region on the left which has an arc and two straight line sides. Let g(6) be the area of the shaded region on the right which is a right triangle. Note that the areas of these two regions will be functions of 6; r=9 is fixed in the problem. 0 f(0) (a) Find a formula for f(6)= | | (b)Find a formula for g(6)= lim ƒ (6) (c) 80 = lim g (0) (d) 80 = lim (e) [f(8)/g(6)]= 0 g(0)arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=_niP0JaOgHY;License: Standard YouTube License, CC-BY