
Concept explainers
Calculate the Riemann sum for the given
a) Lower-left vertex
b) Midpoint of rectangle
Then calculate the exact value of the double integral.
Answer to Problem 1CRE
Solution:
(a) The Riemann sum for the given double integral using lower-left vertices is 240.
(b)The Riemann sum for the given double integral using midpoints is 510.
And the exact value of the double integral is 520.
Explanation of Solution
Given:
The integral:
Formulas:
Where
Calculations:
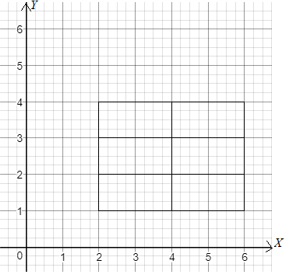
From the given integral, we can observe that and . Since our aim is to find , we need to divide the rectangle into subrectangles. The length and width of each subrectangle are calculated as follows:
Therefore, the area of each subrectangle is .
The subrectangles are shown in Image 1.
Image 1:
(a) Using Lower-left vertex
Here, we use the lower-left vertices of each subrectangleto find the Riemann sum . Notice that the lower-left vertices are and are shown in Image 2.
Image 2:
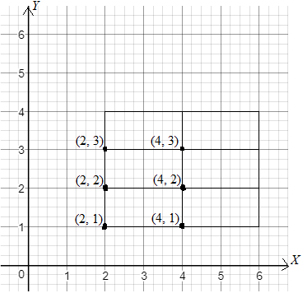
Thus,
(b) Using Midpoint of Rectangle:
Here, we use the midpoints of each subrectangle to find the Riemann sum . Notice that the midpoints are and are shown in Image 3.
Image 3:
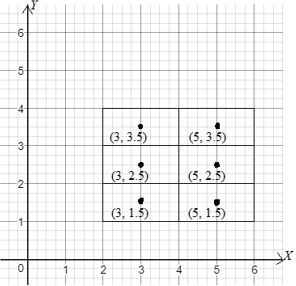
Thus,
To calculate the exact value of the integral:
Conclusion:
Thus,
(a) The Riemann sum for the given double integral using lower-left vertices is 240.
(b)The Riemann sum for the given double integral using midpoints is 510.
And the exact value of the double integral is 520.
Want to see more full solutions like this?
Chapter 16 Solutions
CALCULUS 4E (LL) W/ ACHIEVE ACCESS
- Consider the graphs of y = f(x) and y = g(x) in the given diagram y= f(x). y = g(x) Evaluate (f+g)(2) -5 Determine all for which g(x) < f(x) Determine all for which f(x) +3 = g(x)arrow_forwardI) For what value(s) of x does g(x) = -4? Separate multiple answers with commas as needed. J) Give the interval(s) of such that g(x) > 0. Use the union symbol between multiple intervals. K) Give the interval(s) of such that g(x) <0. Use the union symbol between multiple intervals.arrow_forwardneed help on Barrow_forward
- 4. Use the properties of limits to help decide whether each limit exists. If a limit exists, fi lim (2x²-4x+5) a) x-4 b) lim 2 x²-16 x-4x+2x-8arrow_forward7. The concentration of a drug in a patient's bloodstream h hours after it was injected is given by 0.17 h Ah= h²+2' Find and interpret lim A(h). Remember, the answers to word problems should always be given in a complete h→00 sentence, with proper units, in the context of the problem.arrow_forward#2arrow_forward
- 2. We want to find the inverse of f(x) = (x+3)² a. On the graph at right, sketch f(x). (Hint: use what you know about transformations!) (2 points) b. What domain should we choose to get only the part of f (x) that is one- to-one and non-decreasing? Give your answer in inequality notation. (2 points) - c. Now use algebra to find f¯¹ (x). (2 points) -4- 3- 2 1 -4 -3 -2 -1 0 1 -1- -2- --3- -4 -N- 2 3 4arrow_forward1. Suppose f(x) = 2 4 == x+3 and g(x) = ½-½. Find and fully simplify ƒ(g(x)). Be sure to show all x your work, write neatly so your work is easy to follow, and connect your expressions with equals signs. (4 points)arrow_forwardFind the ane sided limit lim 2 x+1-3x-3arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
