Chapter 15.4, Problem 28ES

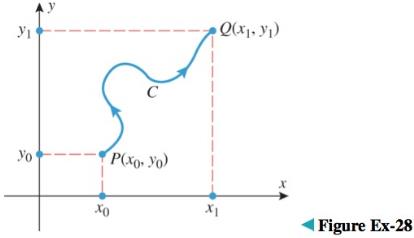
In the accompanying figure, C is a smooth oriented curve from $P\left(x_0,y_0\right)\text{to}Q\left(x_1,y_1\right)$ that is contained inside the rectangle with corners at the origin and Q and outside the rectangle with corners at the origin and P.

(a) What region in the figure has area ${\displaystyle {\int }_{C}xdy?}$

(b) What region in the figure has area ${\displaystyle {\int }_{C}ydx?}$

(c) Express ${\displaystyle {\int }_{C}xdy+{\displaystyle {\int }_{C}ydx}}$ in terms of the coordinates of P and Q.

(d) Interpret the result of part (c) in terms of the Fundamental Theorem of Line Integrals.

(e) Interpret the result in part (c) in terms of integration by parts.