Chapter 15, Problem 84CP

A smaller disk of radius r and mass m is attached rigidly to the face of a second larger disk of radius R and mass M as shown in Figure P15.48. The center of the small disk is located at the edge of the large disk. The large disk is mounted at its center on a frictionless axle. The assembly is rotated through a small angle θ from its equilibrium position and released. (a) Show that the speed of the center of the small disk as it passes through the equilibrium position is

$v=2{\left[\frac{Rg(1-\cos \theta )}{(M/m)+{(r/R)}^2+2}\right]}^{1/2}$

(b) Show that the period of the motion is

$v=2\pi {\left[\frac{(M/2m)+R^2+m{r}^2}{2mgR}\right]}^{1/2}$

Figure P15.48

To determine

To show: The speed of the center of the small disk as it passes through the equilibrium position is $v=2{\left[\frac{Rg\left(1-\cos \theta \right)}{\left(M/m\right)+{\left(r/R\right)}^2+2}\right]}^{1/2}$.

Answer to Problem 84CP

The speed of the center of the small disk as it passes through the equilibrium position is $2{\left[\frac{Rg\left(1-\cos \theta \right)}{\left(M/m\right)+{\left(r/R\right)}^2+2}\right]}^{1/2}$.

Explanation of Solution

Given info: The radius of the smaller disk is $r$, the mass of the smaller disk is $m$, the radius of larger disk is $R$, the mass of the larger disk is $M$ and the angle at which assembly is rotated is $\theta$.

Consider the figure for the given situation.

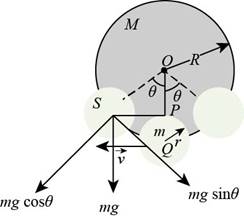
Figure (1)

The loss in the potential energy at $S$ is converted into kinetic energy at $Q$.

Write the expression for the height of the smaller disk from the centre point $O$.

$h=OB-OA$

Here,

$h$ is the height of the smaller disk from the centre point $O$.

Substitute $R$ for $OB$ and $R\cos \theta$ for $OA$ in above equation to find $h$.

$\begin{array}{c}h=R-R\cos \theta \\ =R\left(1-\cos \theta \right)\end{array}$

Here,

$R$ is the radius of larger disk.

$\theta$ is the angle at which assembly is rotated.

Write the expression for the loss in potential energy.

$E_{\text{potential}}=mgh$

Here,

$E_{\text{potential}}$ is the loss in potential energy.

$m$ is mass of the smaller disk.

$g$ is the acceleration due to gravity.

Substitute $R\left(1-\cos \theta \right)$ for $h$ in above equation to find $E_{\text{potential}}$.

$E_{\text{potential}}=mgR\left(1-\cos \theta \right)$

Write the expression for the moment of inertia of the larger disk about the cylinder axis.

$I_{\text{larger}\text{disk}}=\frac{M{R}^2}{2}$

Here,

$I_{\text{larger}\text{disk}}$ is the moment of inertia of the larger disk about the cylinder axis.

$M$ is mass of the larger disk.

$R$ is the radius of larger disk.

Write the expression for the moment of inertia of the smaller disk about the cylinder axis.

$I_{\text{small}\text{disk}}=\frac{m{r}^2}{2}$

Here,

$I_{\text{small}\text{disk}}$ is the moment of inertia of the smaller disk about the cylinder axis.

$r$ is the radius of smaller disk.

Write the expression for the moment of inertia of the smaller disk about the diameter.

$I^{\prime }=m{R}^2$

Here,

$I^{\prime }$ is the moment of inertia of the smaller disk about the diameter.

Write the expression for the net moment of inertia of the two disk system.

$I=I_{\text{larger}\text{disk}}+I_{\text{small}\text{disk}}+I^{\prime }$

Here,

$I$ is the net moment of inertia of the two disk system.

Substitute $\frac{M{R}^2}{2}$ for $I_{\text{larger}\text{disk}}$, $\frac{m{r}^2}{2}$ for $I_{\text{small}\text{disk}}$ and $m{R}^2$ for $I^{\prime }$ in the above equation to find $I$.

$I=\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2$

Write the expression for the angular velocity of the disk.

$\omega =\frac{v}{R}$

Here,

$\omega$ is the angular velocity of the disk.

$v$ is the linear velocity of the disk.

The gain in kinetic energy of the system is equal to the sum of the center of mass of the small disk, the rotational energy of the larger disk and the rotational energy of the smaller disk about $O$.

Write the expression for the gain in kinetic energy of the system.

$E_{\text{kinetic}}=\frac{1}{2}I{\omega }^2$

Here,

$E_{\text{kinetic}}$ is the gain in kinetic energy of the system.

Substitute $\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right)$ for $I$ and $\frac{v}{R}$ for $\omega$ in the above equation to find $E_{\text{kinetic}}$.

$E_{\text{kinetic}}=\frac{1}{2}\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right){\left(\frac{v}{R}\right)}^2$

Apply conservation law of energy.

$E_{\text{potential}}=E_{\text{kinetic}}$

Substitute $\frac{1}{2}\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right){\left(\frac{v}{R}\right)}^2$ for $E_{\text{kinetic}}$ and $mgR\left(1-\cos \theta \right)$ for $E_{\text{potential}}$ in the above equation.

$\begin{array}{c}mgR\left(1-\cos \theta \right)=\frac{1}{2}\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right){\left(\frac{v}{R}\right)}^2\\ {\left(\frac{v}{R}\right)}^2=\frac{2mgR\left(1-\cos \theta \right)}{\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right)}\\ v^2=\frac{2mgR\left(1-\cos \theta \right)}{\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right)}{R}^2\\ v={\left[\frac{2mgR\left(1-\cos \theta \right)}{\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right)}\right]}^{1/2}R\end{array}$

Further solve the above equation.

$\begin{array}{c}v={\left[\frac{2gR\left(1-\cos \theta \right)}{\frac{R^2}{2}\left(\frac{M}{m}+\frac{m{r}^2}{m{R}^2}+\frac{m}{m}\right)}\right]}^{1/2}R\\ ={\left[\frac{4gR\left(1-\cos \theta \right)}{\left(M/m\right)+{\left(r/R\right)}^2+2}\right]}^{1/2}\\ =2{\left[\frac{Rg\left(1-\cos \theta \right)}{\left(M/m\right)+{\left(r/R\right)}^2+2}\right]}^{1/2}\end{array}$

Conclusion:

Therefore, the speed of the center of the small disk as it passes through the equilibrium position is $2{\left[\frac{Rg\left(1-\cos \theta \right)}{\left(M/m\right)+{\left(r/R\right)}^2+2}\right]}^{1/2}$.

To determine

To show: The period of the motion is $T=2\pi {\left[\frac{\left(M+2m\right)R^2+m{r}^2}{2mgR}\right]}^{1/2}$.

Answer to Problem 84CP

The period of the motion is $2\pi {\left[\frac{\left(M+2m\right)R^2+m{r}^2}{2mgR}\right]}^{1/2}$.

Explanation of Solution

Given info: The radius of the smaller disk is $r$, the mass of the smaller disk is $m$, the radius of larger disk is $R$, the mass of the larger disk is $M$ and the angle at which assembly is rotated is $\theta$.

As the value of angle at which assembly is rotated is very small.

$\sin \theta \approx \theta$

From the figure, write the expression for the equation of motion.

$I\frac{d^2\theta }{d{t}^2}=-mgR\sin \theta$

Substitute $\theta$ for $\sin \theta$ in above equation.

$\begin{array}{c}I\frac{d^2\theta }{d{t}^2}=-mgR\theta \\ \frac{d^2\theta }{d{t}^2}+\frac{mgR}{I}\theta =0\end{array}$ (1)

Write the expression for the equation of motion.

$\frac{d^2\theta }{d{t}^2}+{\omega }^2\theta =0$ (2)

Compare equations (1) and (2).

$\begin{array}{c}{\omega }^2=\frac{mgR}{I}\\ \omega =\sqrt{\frac{mgR}{I}}\end{array}$

Formula to calculate the period of the motion is,

$\begin{array}{c}\omega =\frac{2\pi }{T}\\ T=\frac{2\pi }{\omega }\end{array}$

Here,

$T$ is the period of the motion.

Substitute $\sqrt{\frac{mgR}{I}}$ for $\omega$ in the above equation.

$T=\frac{2\pi }{\sqrt{\frac{mgR}{I}}}$

Substitute $\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right)$ for $I$ in the above equation.

$\begin{array}{c}T=\frac{2\pi }{\sqrt{\frac{mgR}{\left(\frac{M{R}^2}{2}+\frac{m{r}^2}{2}+m{R}^2\right)}}}\\ =2\pi {\left[\frac{M{R}^2+m{r}^2+2m{R}^2}{2mgR}\right]}^{1/2}\\ =2\pi {\left[\frac{\left(M+2m\right)R^2+m{r}^2}{2mgR}\right]}^{1/2}\end{array}$

Conclusion:

Therefore, the period of the motion is $2\pi {\left[\frac{\left(M+2m\right)R^2+m{r}^2}{2mgR}\right]}^{1/2}$.