Chapter 15, Problem 30P

To determine

Find the member end moments and reaction for the frames.

Answer to Problem 30P

The end moments at the member AC $\left(M_{AC}\right)$, CA $\left(M_{CA}\right)$, CD $\left(M_{CD}\right)$, DC $\left(M_{DC}\right)$, DB $\left(M_{DB}\right)$ and BD $\left(M_{BD}\right)$ are $\underset{\_}{47.3\text{k}\cdot \text{ft}}$, $\underset{\_}{19\text{k}\cdot \text{ft}}$, $\underset{\_}{-19\text{k}\cdot \text{ft}}$, $\underset{\_}{-103.4\text{k}\cdot \text{ft}}$, $\underset{\_}{103.4\text{k}\cdot \text{ft}}$ and $\underset{\_}{89.4\text{k}\cdot \text{ft}}$ respectively and the reactions at the point A$\left(A_x\right)\left(A_y\right)$ and B$\left(B_x\right)\left(B_y\right)$ are $\underset{\_}{\left(0.05\text{k}\leftarrow \right),\left(16.34\text{k}\uparrow \right)}$ and $\underset{\_}{\left(19.95\text{k}\leftarrow \right),\left(31.65\text{k}\uparrow \right)}$ respectively.

Explanation of Solution

Fixed end moment:

Formula to calculate the fixed moment for UDL is $\frac{W{L}^2}{12}$.

Calculation:

Consider the flexural rigidity EI of the frame is constant.

Show the free body diagram of the entire frame as in Figure 1.

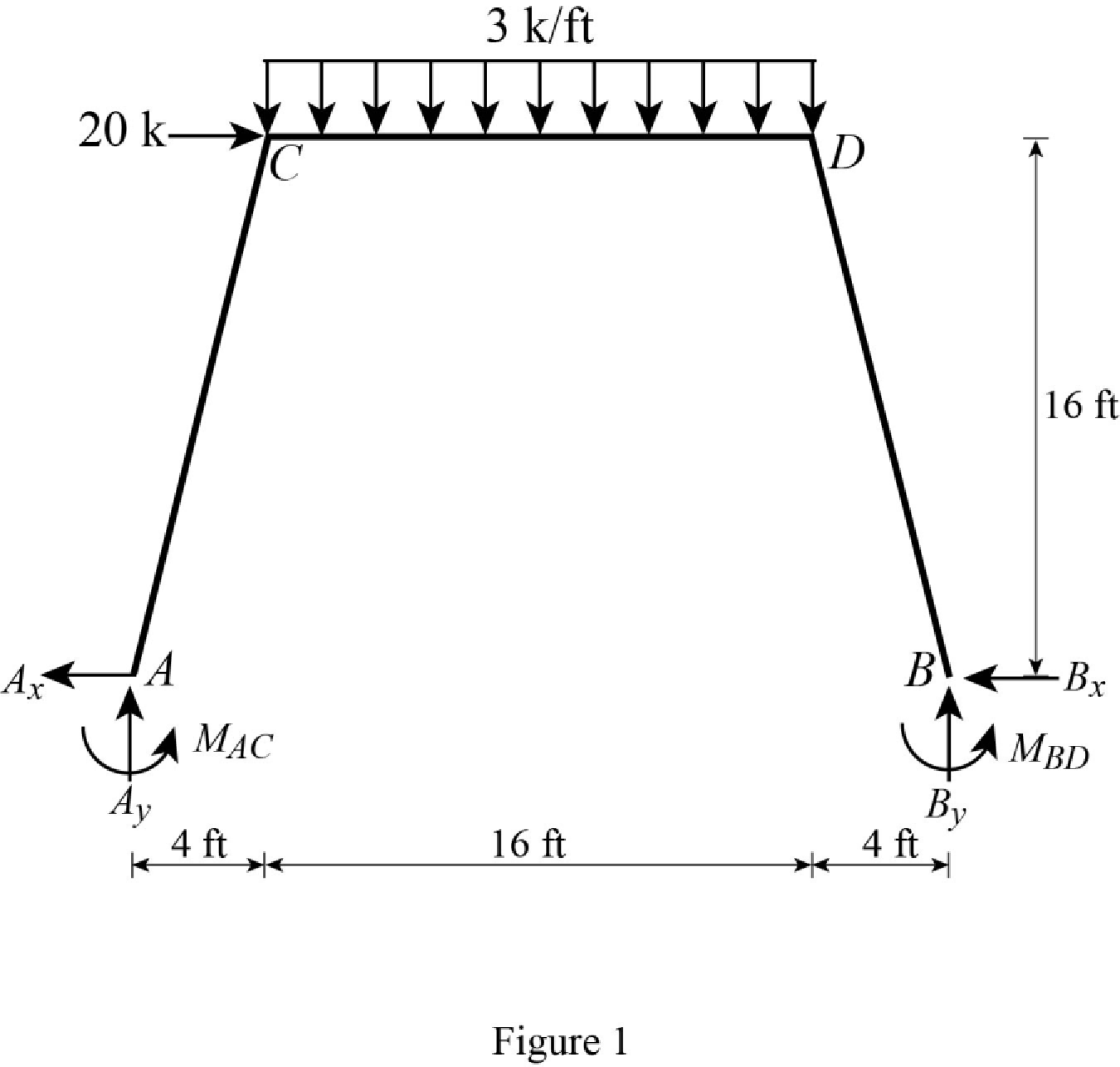
Refer Figure 1,

Calculate the fixed end moment for AC.

${\text{FEM}}_{AC}=0$

Calculate the fixed end moment for CA.

${\text{FEM}}_{CA}=0$

Calculate the fixed end moment for CD.

$\begin{array}{c}{\text{FEM}}_{CD}=\frac{3\times {16}^2}{12}\\ =64\text{k}\cdot \text{ft}\end{array}$

Calculate the fixed end moment for DC.

${\text{FEM}}_{DC}=-64\text{k}\cdot \text{ft}$

Calculate the fixed end moment for DB.

${\text{FEM}}_{DB}=0\text{k}\cdot \text{ft}$

Calculate the fixed end moment for BD.

${\text{FEM}}_{BD}=0\text{k}\cdot \text{ft}$

Chord rotations:

Show the free body diagram of the chord rotation of the frame as in Figure 2.

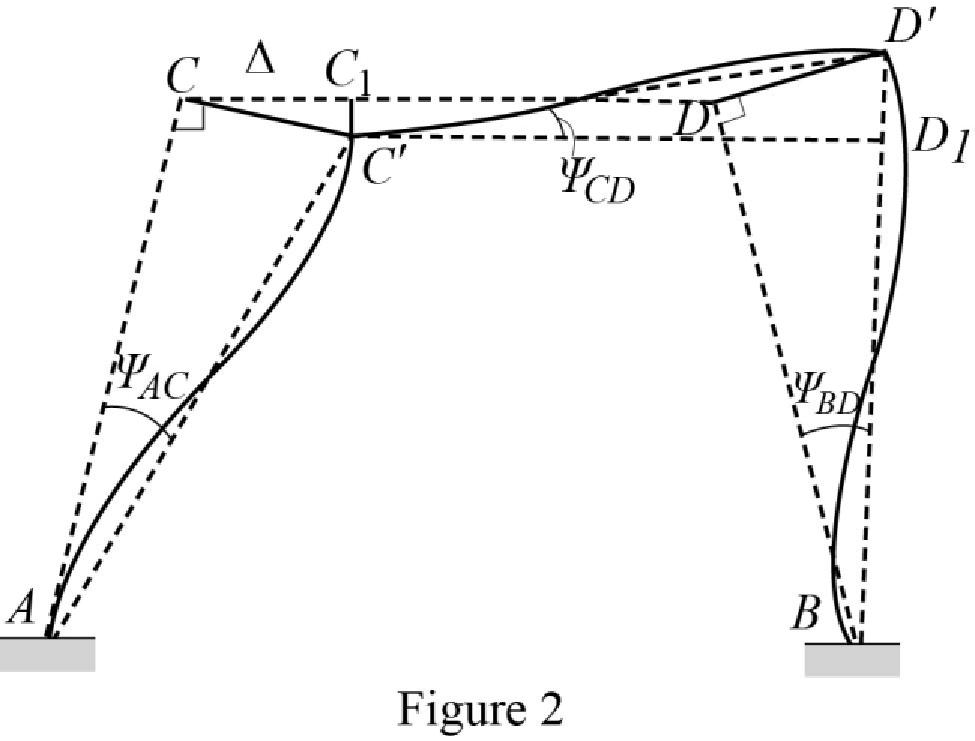
Calculate the length of AC by using Pythagoras theorem.

$\begin{array}{c}{L}_{AC}=\sqrt{\left({16}^2\right)+\left(4^2\right)}\\ =16.49\text{ft}\end{array}$

Calculate the length of BD by using Pythagoras theorem.

$\begin{array}{c}{L}_{BD}=\sqrt{\left({16}^2\right)+\left(4^2\right)}\\ =16.49\text{ft}\end{array}$

Calculate the chord rotation of the frame AC.

$\begin{array}{c}{\psi }_{AC}=-\frac{C{C}^{\prime }}{L_{AC}}\\ =-\frac{\frac{\sqrt{17}}{4}\Delta }{16.49}\\ =-0.0625\Delta \end{array}$

Calculate the chord rotation of the frame BD.

$\begin{array}{c}{\psi }_{BD}=-\frac{D{D}^{\prime }}{L_{BD}}\\ =-\frac{\frac{\sqrt{17}}{4}\Delta }{5}\\ =-0.0625\Delta \end{array}$

Calculate the chord rotation of the frame CD.

$\begin{array}{c}{\psi }_{CD}=-\frac{D_1{D}^{\prime }}{L_{CD}}\\ =\frac{2\left(\frac{1}{4}\right)\Delta }{16}\\ =0.03125\Delta \end{array}$

Calculate the slope deflection equation for the member AC.

$M_{AC}=\frac{2EI}{L}\left(2{\theta }_A+{\theta }_C-3{\psi }_{AC}\right)+{\text{FEM}}_{AC}$

Substitute 16.49 ft for L, 0 for ${\theta }_A$, $-0.0625\Delta$ for ${\psi }_{AC}$, and 0 for ${\text{FEM}}_{AC}$.

$\begin{array}{c}{M}_{AC}=\frac{2EI}{16.49}\left(2\left(0\right)+{\theta }_C-3\left(-0.0625\Delta \right)\right)+0\\ =0.121EI{\theta }_C+0.0227EI\Delta \end{array}$        (1)

Calculate the slope deflection equation for the member CA.

$M_{CA}=\frac{2EI}{L}\left(2{\theta }_C+{\theta }_A-3{\psi }_{CA}\right)+{\text{FEM}}_{CA}$

Substitute 16.49 ft for L, 0 for ${\theta }_A$, $-0.0625\Delta$ for ${\psi }_{CA}$, and 0 for ${\text{FEM}}_{CA}$.

$\begin{array}{c}{M}_{CA}=\frac{2EI}{16.49}\left(2{\theta }_C+0-3\left(-0.0625\Delta \right)\right)-0\\ =0.2426EI{\theta }_C+0.0227EI\Delta \end{array}$        (2)

Calculate the slope deflection equation for the member CD.

$M_{CD}=\frac{2EI}{L}\left(2{\theta }_C+{\theta }_D-{\psi }_{CD}\right){\text{+FEM}}_{CD}$

Substitute 16 ft for L, $0.03125\Delta$ for ${\psi }_{CD}$, and $64\text{k}\cdot \text{ft}$ for ${\text{FEM}}_{CD}$.

$\begin{array}{c}{M}_{CD}=\frac{2EI}{16}\left(2{\theta }_C+{\theta }_D-3\left(0.03125\Delta \right)\right)+64\\ =0.25EI{\theta }_C+0.125EI{\theta }_D-0.01172EI\Delta +64\end{array}$        (3)

Calculate the slope deflection equation for the member DC.

$M_{DC}=\frac{2EI}{L}\left(2{\theta }_D+{\theta }_C-{\psi }_{DC}\right){\text{+FEM}}_{DC}$

Substitute 16 ft for L, $0.03125\Delta$ for ${\psi }_{DC}$, and $-64\text{k}\cdot \text{ft}$ for ${\text{FEM}}_{DC}$.

$\begin{array}{c}{M}_{DC}=\frac{2EI}{16}\left(2{\theta }_D+{\theta }_C-3\left(0.15\Delta \right)\right)-64\\ =0.125EI{\theta }_C+0.25EI{\theta }_D-0.01172EI\Delta -64\end{array}$        (4)

Calculate the slope deflection equation for the member DB.

$M_{DB}=\frac{2EI}{L}\left(2{\theta }_D+{\theta }_B-3{\psi }_{DB}\right){\text{+FEM}}_{DB}$

Substitute 16.49 ft for L, 0 for ${\theta }_B$, $-0.0625\Delta$ for ${\psi }_{DB}$, and $0\text{k}\cdot \text{ft}$ for ${\text{FEM}}_{DB}$.

$\begin{array}{c}{M}_{DB}=\frac{2EI}{16.49}\left(2{\theta }_D+\left(0\right)-3\left(-0.0625\Delta \right)\right)+0\\ =0.2426EI{\theta }_D+0.0227EI\Delta \end{array}$        (5)

Calculate the slope deflection equation for the member BD.

$M_{BD}=\frac{2EI}{L}\left(2{\theta }_B+{\theta }_D-3{\psi }_{BD}\right){\text{+FEM}}_{BD}$

Substitute 16.49 ft for L, 0 for ${\theta }_B$, $-0.0625\Delta$ for ${\psi }_{BD}$, and $0\text{k}\cdot \text{ft}$ for ${\text{FEM}}_{BD}$.

$\begin{array}{c}{M}_{BD}=\frac{2EI}{16.49}\left({\theta }_D+2\left(0\right)-3\left(-0.0625\Delta \right)\right)+0\\ =0.121EI{\theta }_D+0.0227EI\Delta \end{array}$        (6)

Write the equilibrium equation as below.

$M_{CA}+M_{CD}=0$

Substitute equation (2) and equation (3) in above equation.

$\begin{array}{l}0.2426EI{\theta }_C+0.0227EI\Delta +0.25EI{\theta }_C+0.125EI{\theta }_D-0.01172EI\Delta +64=0\\ 0.4926EI{\theta }_C+0.125EI{\theta }_D+0.011EI\Delta =-64\end{array}$        (7)

Write the equilibrium equation as below.

$M_{DC}+M_{DB}=0$

Substitute equation (4) and equation (5) in above equation.

$\begin{array}{l}0.125EI{\theta }_C+0.25EI{\theta }_D-0.01172EI\Delta -64+0.2426EI{\theta }_D+0.0227EI\Delta =0\\ 0.125EI{\theta }_C+0.4926EI{\theta }_D+0.011EI\Delta =64\end{array}$        (8)

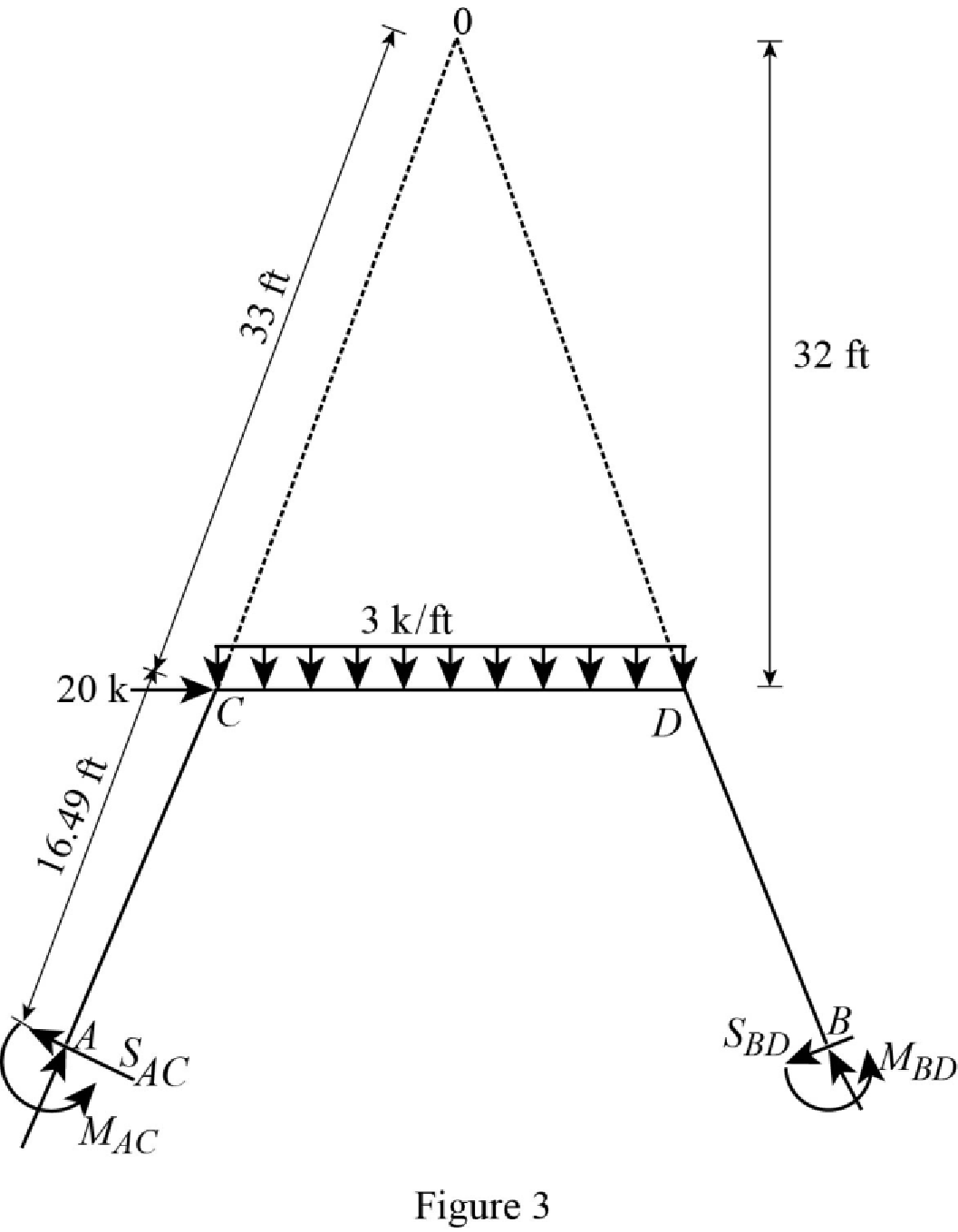
Show the free body diagram of the entire frame due to sway force as in Figure 3.

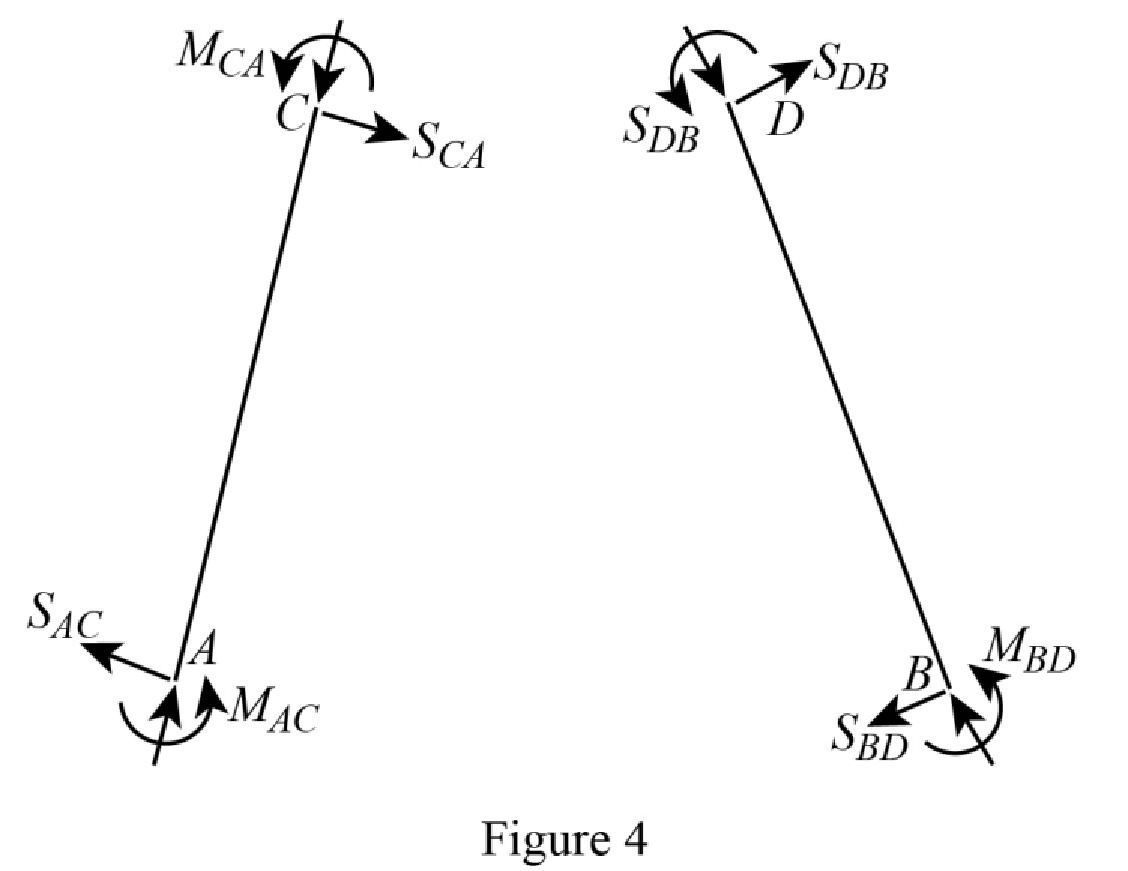
Show the free body diagram of the frame due to sway force as in Figure 4.

Calculate the horizontal reaction at the member AC due to sway force by taking moment about point A.

$\begin{array}{l}{\displaystyle \sum M_A=0}\\ \left(-S_{AC}\times 16.49\right)+M_{AC}+M_{CA}=0\\ S_{AC}=\frac{M_{AC}+M_{CA}}{16.49}\end{array}$

Calculate the horizontal reaction at the member BD due to sway force by taking moment about point B.

$\begin{array}{l}{\displaystyle \sum M_A=0}\\ \left(-S_{BD}\times 16.49\right)+M_{BD}+M_{DB}=0\\ S_{BD}=\frac{M_{BD}+M_{DB}}{16.49}\end{array}$

Calculate the reaction of the support C and support D due to sway force by taking the moment about O.

$\begin{array}{l}{\displaystyle \sum M_0=0}\\ M_{AC}+M_{BD}-S_{AC}\left(16.49+33\right)-S_{BD}\left(16.49+33\right)+\left(20\times 32\right)=0\\ M_{AC}+M_{BD}-\left[\frac{M_{AC}+M_{CA}}{16.49}\left(49.49\right)\right]-\left[\frac{M_{BD}+M_{DB}}{16.49}\left(49.49\right)\right]+640=0\\ M_{AC}+M_{BD}-3M_{AC}-3M_{CA}-3M_{BD}-3M_{DB}+640=0\\ -2M_{AC}-2M_{BD}-3M_{CA}-3M_{DB}=-640\end{array}$

Substitute equation (1), equation (2), equation (5), and equation (6) in above equation.

$\begin{array}{l}\left\{\begin{array}{l}-2\left(0.121EI{\theta }_C+0.0227EI\Delta \right)-3\left(0.2426EI{\theta }_C+0.0227EI\Delta \right)\\ -2\left(0.121EI{\theta }_D+0.0227EI\Delta \right)-3\left(0.2426EI{\theta }_D+0.0227EI\Delta \right)\end{array}\right\}=-640\\ \left\{\begin{array}{l}-0.242EI{\theta }_C-0.0454EI\Delta -0.7278EI{\theta }_C-0.0681EI\Delta \\ -0.0242EI{\theta }_D-0.0454EI\Delta -0.7278EI{\theta }_D-0.0681EI\Delta \end{array}\right\}=-640\\ -0.9698{\theta }_C-0.9698EI{\theta }_D-0.227EI\Delta =-640\\ 0.9698{\theta }_C+0.9698EI{\theta }_D+0.227EI\Delta =640\end{array}$        (9)

Solve the equation (7), equation (8), and equation (9).

$\begin{array}{l}{\theta }_C=\frac{-233.3}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}\\ {\theta }_D=\frac{114.9}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}\\ \Delta =\frac{3325.5}{EI}\text{k}\cdot {\text{ft}}^{\text{3}}\end{array}$

Calculate the moment about AC.

Substitute $\frac{-233.3}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}$ for ${\theta }_C$ and $\frac{3325.5}{EI}\text{k}\cdot {\text{ft}}^{\text{3}}$ for $\Delta$ in equation (1).

$\begin{array}{c}{M}_{AC}=0.121EI\left(\frac{-233.3}{EI}\right)+0.0227EI\left(\frac{3325.5}{EI}\right)\\ =47.3\text{k}\cdot \text{ft}\end{array}$

Calculate the moment about CA.

Substitute $\frac{-233.3}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}$ for ${\theta }_C$ and $\frac{3325.5}{EI}\text{k}\cdot {\text{ft}}^{\text{3}}$ for $\Delta$ in equation (1).

$\begin{array}{c}{M}_{CA}=0.2426EI\left(\frac{-233.3}{EI}\right)+0.0227EI\left(\frac{3325.5}{EI}\right)\\ =19\text{k}\cdot \text{ft}\end{array}$

Calculate the moment about CD.

Substitute $\frac{-233.3}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}$ for ${\theta }_C$, $\frac{114.9}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}$ for ${\theta }_D$, and $\frac{3325.5}{EI}\text{k}\cdot {\text{ft}}^{\text{3}}$ for $\Delta$ in equation (3).

$\begin{array}{c}{M}_{CD}=0.25EI\left(\frac{-233.3}{EI}\right)+0.125EI\left(\frac{114.9}{EI}\right)-0.01172EI\left(\frac{3325.5}{EI}\right)+64\\ =-19\text{k}\cdot \text{ft}\end{array}$

Calculate the moment about DC.

Substitute $\frac{-233.3}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}$ for ${\theta }_C$, $\frac{114.9}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}$ for ${\theta }_D$ and $\frac{3325.5}{EI}\text{k}\cdot {\text{ft}}^{\text{3}}$ for $\Delta$ in equation (4).

$\begin{array}{c}{M}_{DC}=0.125EI\left(\frac{-233.3}{EI}\right)+0.25EI\left(\frac{114.9}{EI}\right)-0.01172EI\left(\frac{3325.5}{EI}\right)-64\\ =-103.4\text{k}\cdot \text{ft}\end{array}$

Calculate the moment about DB.

Substitute $\frac{114.9}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}$ for ${\theta }_D$ and $\frac{3325.5}{EI}\text{k}\cdot {\text{ft}}^{\text{3}}$ for $\Delta$ in equation (5).

$\begin{array}{c}{M}_{DB}=0.2426EI\left(\frac{114.9}{EI}\right)+0.0227EI\left(\frac{3325.5}{EI}\right)\\ =103.4\text{k}\cdot \text{ft}\end{array}$

Calculate the moment about BD.

Substitute $\frac{114.9}{EI}\text{k}\cdot {\text{ft}}^{\text{2}}$ for ${\theta }_D$ and $\frac{3325.5}{EI}\text{k}\cdot {\text{ft}}^{\text{3}}$ for $\Delta$ in equation (6).

$\begin{array}{c}{M}_{BD}=0.121EI\left(\frac{114.9}{EI}\right)+0.0227EI\left(\frac{3325.5}{EI}\right)\\ =89.4\text{k}\cdot \text{ft}\end{array}$

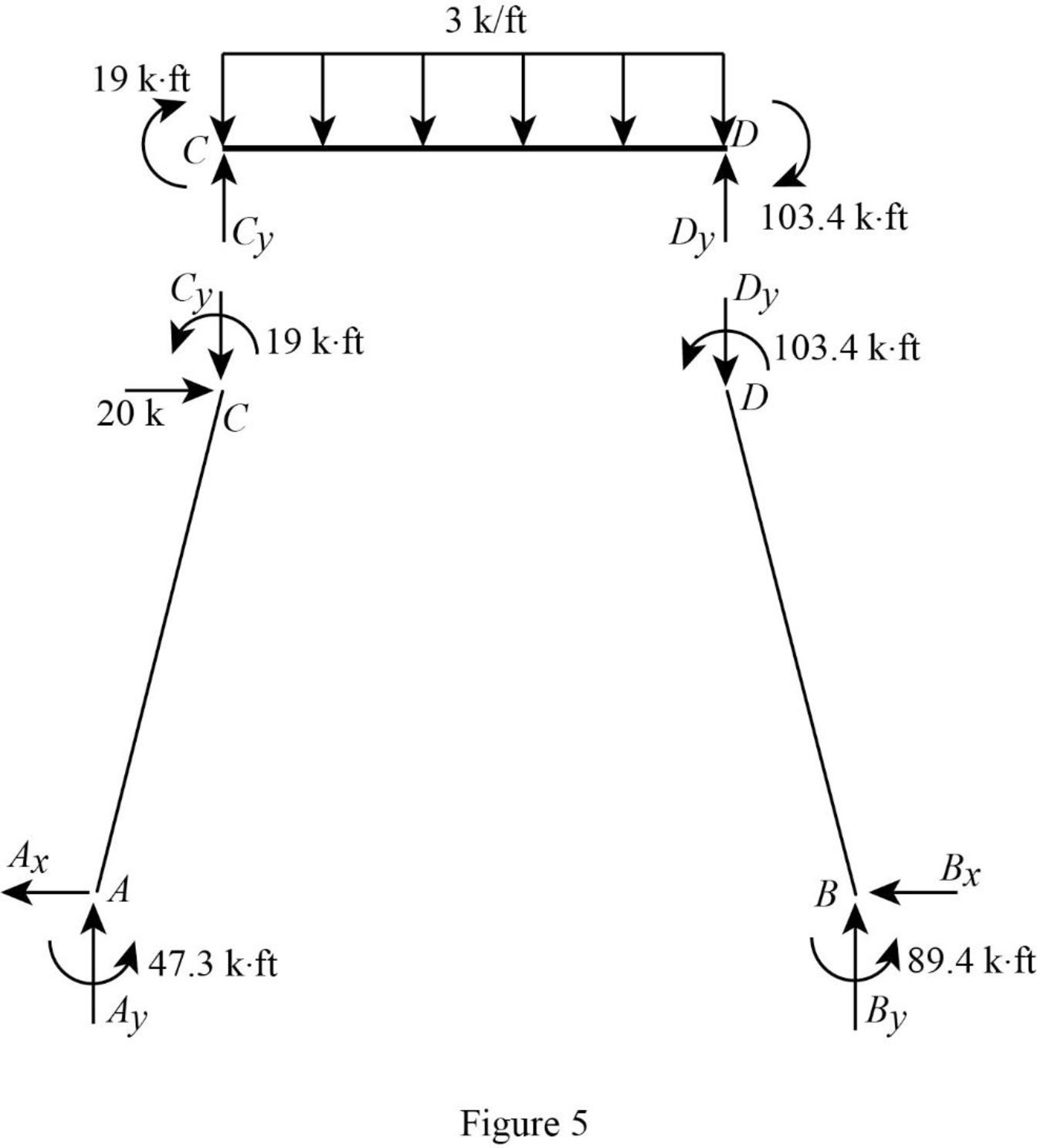
Show the section free body diagram of the member AC, CD and DB as in Figure 5.

Consider the member CD.

Calculate the vertical reaction at the joint D by taking moment about point C.

$\begin{array}{l}+\circlearrowleft {\displaystyle \sum M_C=0}\\ D_y\left(16\right)-\left(3\times 16\times \frac{16}{2}\right)-19-103.4=0\\ D_y\left(16\right)=506.4\\ D_y=\frac{506.4}{16}\\ D_y=31.65\text{k}\uparrow \end{array}$

Calculate the vertical reaction at joint C by resolving the vertical equilibrium.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ D_y+C_y=\left(3\times 16\right)\\ C_y+31.65=48\\ C_y=16.34\text{k}\uparrow \end{array}$

Consider the member AC.

Calculate the vertical reaction at joint A by resolving the vertical equilibrium.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ C_y+A_y=0\\ -16.34+A_y=0\\ A_y=16.34\text{k}\uparrow \end{array}$

Calculate the horizontal reaction at the joint A by taking moment about point C.

$\begin{array}{l}+\circlearrowleft {\displaystyle \sum M_C=0}\\ -A_x\left(16\right)-\left(16.35\times 4\right)+47.3+19=0\\ A_x\left(16\right)=0.9\\ A_x=\frac{0.9}{16}\\ A_x=0.05\text{k}\leftarrow \end{array}$

Consider the member BD.

Calculate the vertical reaction at joint B by resolving the vertical equilibrium.

$\begin{array}{l}+\uparrow {\displaystyle \sum F_y=0}\\ B_y+D_y=0\\ -31.65+B_y=0\\ B_y=31.65\text{k}\uparrow \end{array}$

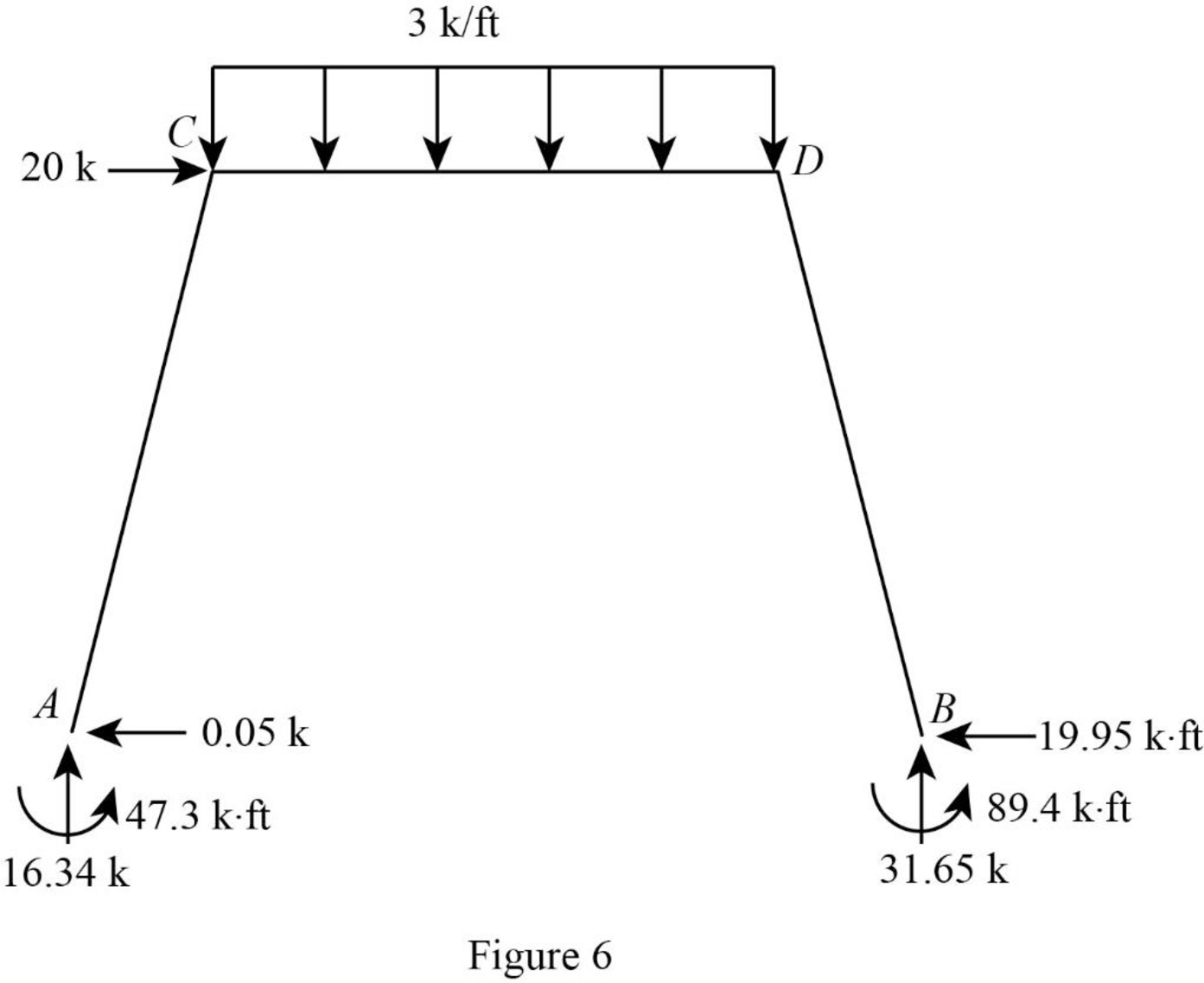
Consider the entire frame.

Calculate the horizontal reaction at the joint B by considering the horizontal equilibrium.

$\begin{array}{l}+\to {\displaystyle \sum F_x=0}\\ B_x+A_x=-20\\ B_x-0.05=-20\\ B_x=19.95\text{k}\leftarrow \end{array}$

Show the reactions of the frame as in Figure 6.