
Find the factors of safety with respect to overturning, sliding, and bearing capacity failure.
Answer to Problem 15.4P
The factor of safety with respect to overturning is
The factor of safety with respect to sliding is
The factor of safety with respect to bearing capacity failure is
Explanation of Solution
Given information:
The cohesion
The unit weight
The friction angle
The unit weight
The cohesion
The unit weight of soil
The friction angle
The backfill angle
Calculation:
Check stability with respect to overturning.
Consider point C as the left end of the toe base as named as C.
Divide the retaining wall into section as in Figure 1.
Sketch the section of the retaining wall as shown in Figure 1.
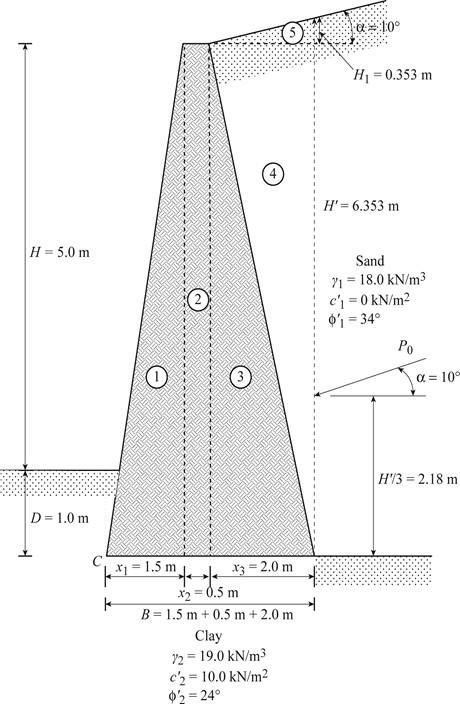
Here,
Refer Table 14.2, “Values of
Take the value of active earth pressure coefficient
Refer Figure 1.
Find the height of the inclined portion of backfill
Substitute 2 m for
Find the total height of the inclined backfill
Here, H is the height of retaining wall and D is the depth to the bottom of the base slab.
Substitute 5.0 m for H, 1.0 m for D, and 0.353 m
Find the active earth pressure
Substitute
Find the vertical component of the active earth pressure
Substitute
Find the horizontal component of the active earth pressure
Substitute
Find the weight of section 1
Here,
Substitute 1.5 m for
Find the moment arm or lever arm
Substitute 1.5 m for
Find the moment about point C
Substitute
Find the weight of section 2
Here,
Substitute 0.5 m for
Find the moment arm or lever arm
Substitute 1.5 m for
Find the moment about point C
Substitute
Find the weight of section 3
Here,
Substitute 2.0 m for
Find the moment arm or lever arm
Substitute 0.5 m for
Find the moment about point C
Substitute
Find the weight of section 4
Here,
Substitute 2.0 m for
Find the moment arm or lever arm
Substitute 2.0 m for
Find the moment about point C
Substitute 108 kN/m for
Find the weight of section 5
Substitute 2 m for
Find the moment arm or lever arm
Substitute 2.0 m for
Find the moment about point C
Substitute
Find the moment arm or lever arm
Substitute 0.5 m for
Find the moment about point C
Substitute
Find the total moment about the point C
Substitute
Find the total vertical load
Substitute
Summarize the values of weight, moment arm from C, and moment about C as shown in Table 1.
| Section | weight | moment arm from C | moment about C |
| 1 | 108 | 1 | 108 |
| 2 | 72 | 1.75 | 126 |
| 3 | 144 | 2.67 | 384.5 |
| 4 | 108 | 3.33 | 359.6 |
| 5 | 6.35 | 3.33 | 21.15 |
| 4 | 75.56 | ||
Find the overturning moment
Substitute
Find the factor of safety
Substitute
Therefore, the factor of safety with respect to overturning is
Check the stability with respect to sliding.
Find the coefficient of passive earth pressure
Substitute
Find the passive earth pressure
Here,
Substitute 1 m for D,
Find the angle of friction
Substitute
Find the factor of safety against sliding
Substitute
Therefore, the factor of safety with respect to sliding is
Check the stability with bearing capacity failure.
Find the eccentricity (e) using the equation:
Substitute 4 m for B,
Check for eccentricity.
Substitute 0.22 m for e and 4 m for B.
The eccentricity is within the limit. Therefore, there is no tensile stress produced at the end of the steel section.
Find the maximum pressure
Substitute
Find the effective breadth
Substitute 4 m for B and 0.22 m for e.
Refer Table 16.2, “Bearing Capacity Factors” in the textbook.
Take the value of bearing capacity factor,
Take the value of bearing capacity factor,
Take the value of bearing capacity factor,
Find the depth factor
Substitute 1 m for D and 4 m for B.
Find the load (q) due the soil in front of heel using the equation:
Substitute
Find the inclination angle of vertical load
Substitute
Find the inclination factor
Substitute
Find the depth factor
Here,
Substitute
The depth factor
Find the inclination factor
Substitute
Find the ultimate bearing capacity of the shallow foundation
Substitute
Find the factor of safety against bearing capacity failure
Substitute
Therefore, the factor of safety with respect to bearing capacity failure is
Want to see more full solutions like this?
Chapter 15 Solutions
EBK FUNDAMENTALS OF GEOTECHNICAL ENGINE
- Sketch the effective stress profile for the silt layer to a depth of 5 meters for a uniform layer of silt having a depth to the water table of 4 m (choose several discrete points with depth and plot by hand). Use Bishop's definition of effective stress for the silt layer, assuming x =S.. Assume a value of G. = 2.65 and that the gravimetric water content of the silt below the water table is 20%. Use the SWRC for the silt from the figure below. Assume that the air pressure is equal to atmospheric pressure (i.e., zero). Consider variations in total unit weight with the degree of saturation in your calculations. 100000 a. 10000 Sand: a = 0.3 kPa, n = 3.0 Silt: a=0.05 kPa, n=2.5 0.01 kPa, n = 1.8 1000 Clay: Matric suction (kPa) 00 100 10 10 1 0.1 ° 20 60 80 40 Saturation (%) 100 10arrow_forwardYou are asked to design a two-story commercial building that has reinforced masonry shear walls as shown below. The height of the parapet above the roof is 2 feet. The walls are to be constructed of 8-inch CMU and are to be fully grouted. The building is assigned to SDC D, and therefore, the walls have to be special RM shear walls according to TMS 402. There are 6 shear walls to resist the lateral seismic force along one principal axis of the building and 4 shear walls along the other axis. The corner walls are flanged walls meeting the requirements in Sec. 5.2.3 of TMS 402-22. The columns carry only gravity loads and no lateral seismic forces. The floor and roof diaphragms are relatively flexible in out-of-plane bending compared to the in-plane flexural stiffness of the walls, so that you can ignore the coupling moments and shear forces exerted by the diaphragms on the walls. However, the in-plane stiffness of the diagrams is high so that their planar deformation can be ignored.…arrow_forwardDevelop a signal design and timing for the intersection shown in the figure below. In each case accommodate both vehicular and pedestrian movements. In general, use the following values for the problem: pedestrian walking speed = 1 [m/s], vehicle deceleration = 3 [m/s²], driver reaction time = 1.5 [s], length of vehicle 6 [m], and level grade = 0. If you need to assume = other variables and parameters to solve this problem clearly state that in your report and explain the reason. 250 1100 One-way Speed limit = 50 [km/h] Pedestrian = 15 per each crosswalk Crosswalk widths = 3 [m] Lane width = 4 [m] Saturation flow = 1800 [veh/h/lane] 1100 70 80 T 200 900arrow_forward
- A pre-timed four-phase signal has critical lane group flow rates for the first three phases of 260, 280, and 310 [veh/h] (saturation flow rates are 2000 [veh/h/In] for all phases). The lost time is known to be 5 seconds for each phase. If the cycle length is 90 seconds, what is the estimated effective green time of the fourth phase?arrow_forwarda. Assume a bus line with N stops, where the distance between stops is S. Free flow speed of the bus is v, with acceleration and deceleration, a. P passengers per stop are boarding and alighting, and the time needed for a passenger to board or alight is T seconds. What is the average speed of a bus? b. Following on part (a), assume the origins of passengers are spread uniformly along the bus route. The destination of all passengers is the last stop. The walking speed of passengers is u. Determine the average travel time (walking + in-vehicle) of passengers. c. Simplify the above equation when N is large enough (approximating N-1/2 by N-1). Consider now that you can decide on S, where you replace N=L/S (L is the length of the route). Find the value of S that minimises the travelling time of the passengers. d. In the same setting as (c), assume that some passengers do not go to the terminal but alight before. Explain if your answer from (c) would increase or decrease and why. If you need…arrow_forwardThe minimum cycle length for an intersection is determined to be 95 seconds. The critical lane group flow ratios were calculated as 0.235, 0.25, 0.17, and 0.125, respectively. Assuming 5 seconds lost per phase, determine which X was used.arrow_forward
- A four-phase traffic signal has critical lane group flow ratios of 0.250, 0.150, 0.225 and 0.125. If the lost time per phase is 4 seconds and a critical intersection v/c of 0.85 is desired, calculate the minimum cycle length and the phase effective green times such that the lane group v/c ratios are equalized.arrow_forwardA pre-timed four-phase signal has critical lane group flow rates for the first three phases of 260, 280, and 310 [veh/h] (saturation flow rates are 2000 [veh/h/ln] for all phases). The lost time is known to be 5 seconds for each phase. If the cycle length is 90 seconds, what is the estimated effective green time of the fourth phase?arrow_forwardPLEASE SOLVE THE QUESTIONS IN THE PICTURE, make sure you show all of your work please. Thank you for your help!arrow_forward
- Please solve the following question in the picture, make sure you show all of your work and formulas you use. Thank you so much for your help!arrow_forwardDetermine all the quantities mentioned. Show complete solution using Mohr's Circle only.arrow_forwardAnswer the following questions please.arrow_forward
 Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Fundamentals of Geotechnical Engineering (MindTap...Civil EngineeringISBN:9781305635180Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning
Principles of Geotechnical Engineering (MindTap C...Civil EngineeringISBN:9781305970939Author:Braja M. Das, Khaled SobhanPublisher:Cengage Learning Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781305081550Author:Braja M. DasPublisher:Cengage Learning



