Chapter 15, Problem 13P

In a classic study, Loftus and Palmer (1974) investigated the relationship between memory for eyewitnesses and the questions they are asked. In the study, participants watched a film of an automobile accident and then were questioned about the accident. One group was asked how fast the cars were going when they "smashed into" each other. A second group was asked about the speed when the ears "hit" each other and a third group was not asked any question about the speed of the ears. A week later, the participants returned to answer additional questions about the accident, including whether they recalled seeing any broken glass. Although there was no broken glass in the film, several students claimed to remember seeing it. The following table shows the Frequency distribu­tion of responses for each group.

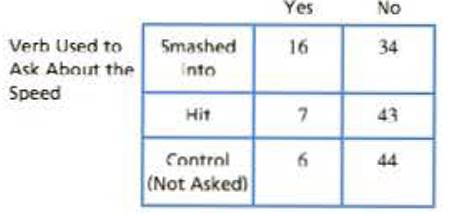
1. a. Does the proportion of participants who claim to remember broken glass differ significantly from group to group? Test with or α = .05
2. b. Compute Cramér's V to measure the size of the treatment effect.
3. c. Describe how the phrasing of the question influenced the participants' memories.
4. d. Write a sentence demonstrating how the outcome of the hypothesis lest and the measure of effect size would be reported in a journal article

To determine

To check: Whether the proportions of participants who claim to remember broken glass differ significantly from group to group for the given question.

Answer to Problem 13P

Reject null and conclude that proportion of participants who claim to remember broken glass differ significantly from group to group.

Explanation of Solution

Given info:

A sample of 150 students were involved in a study based on “the response they gave regarding the broken glass or verb used for speed”. The distribution is given in the question. Use $\alpha =0.05$ to test the claim.

Calculations:

Step 1: Null Hypothesis and Alternate Hypothesis are:

$H_0:$ Proportion of participants who claim to remember broken glass don’t differ significantly from group to group.

$H_1:$ Proportion of participants who claim to remember broken glass differ significantly from group to group

Step 2: For the given sample, degrees of freedom equals:

$\begin{array}{c}df=(R-1)(C-1) \text{where R equals number of rows and C equals columns}\\ =(3-1)(2-1)\\ =2\end{array}$

With $\alpha =0.05$ and $df=2$, the critical value (CV)  is obtained from the ${\chi }^2-table$ as

${\chi }^2=5.991$

Step 3: ${\chi }^2-statistics$ is calculated as:

${\chi }^2={\displaystyle \sum \frac{{(f_o-f_e)}^2}{f_e}}$

The formula to calculate expected frequency is:

$f_e=\frac{f_c{f}_r}{n}{\text{where f}}_{\text{r}}{\text{ is row frequency and f}}_{\text{c}}\text{ is column frequency}$

Substitute $n=600$ in the above formula and compute respective values of expected frequencies:

For the category “smashed into”, the expected frequencies are:

$\begin{array}{c}{f}_{e,yes}=\frac{29\times 50}{150}\\ f_{e,no}=\frac{121\times 50}{150}\end{array}$

For the category “Hit”, the expected frequencies are:

$\begin{array}{c}{f}_{e,yes}=\frac{29\times 50}{150}\\ f_{e,no}=\frac{121\times 50}{150}\end{array}$

Similarly, for the category “control”, the expected frequencies are:

$\begin{array}{c}{f}_{e,yes}=\frac{29\times 50}{150}\\ f_{e,no}=\frac{121\times 50}{150}\end{array}$

The observed and expected frequency is given below:

	Yes	No	Total
Smashed into	16 (9.66)	34 (40.33)	50
Hit	7 (9.66)	43 (40.33)	50
Control (not asked)	6 (9.66)	44 (40.33)	50
Total	29	121	150

Here the values within the braces are the expected frequencies.

Finally substitute the values in the ${\chi }^2$-statistics formula as:

$\begin{array}{c}{\chi }^2=\frac{{(16-9.66)}^2}{9.66}+\frac{{(7-9.66)}^2}{9.66}+\frac{{(6-9.66)}^2}{9.66}+\frac{{(34-40.33)}^2}{40.33}+\frac{{(43-40.33)}^2}{40.33}+\frac{{(44-40.33)}^2}{40.33}\\ =\frac{40.19}{9.66}+\frac{7.07}{9.66}+\frac{13.39}{9.66}+\frac{40.06}{40.33}+\frac{7.12}{40.33}+\frac{13.46}{40.33}\\ =6.27+1.50\\ =7.77\end{array}$

Step 4: Rejection rule:

Reject $H_0$ when ${\chi }^2\text{-statistics}>\text{CV}$.

Since ${\chi }^2\text{-statistics}(=7.77)>\text{critical\_value}(=5.991)$, reject the null hypothesis.

Step 5: Conclusion

Reject the null hypothesis and conclude that proportion of participants who claim to remember broken glass differ significantly from group to group.

To determine

To find: The value of Cramer’s V to measure the size of the treatment effect.

Answer to Problem 13P

The value of Cramer’s v is 0.227

Explanation of Solution

Calculations:

The formula for Cramer’s V is:

$Cramer’sV=\sqrt{\frac{{\chi }^2}{(d{f}^{\ast })n}}$

Here,

$\begin{array}{c}df=\min (R-1,C-1)\\ =2-1\\ =1\end{array}$

Substitute 7.77 for ${\chi }^2$, 150 for $n$ and 1 for $d{f}^{\ast }$,

$\begin{array}{c}Cramer’sV=\sqrt{\frac{7.77}{1\times 150}}\\ =0.227\end{array}$

Hence, value of Cramer’s V is 0.227

To determine

To describe: How does the phrasing of the question influence the participant’s memories.

Answer to Problem 13P

The phrasing of question influenced the participants memories little bit.

Explanation of Solution

Cramer’s V is used as post-test to determine strengths of association once the chi-square has determined significance. A value of 0.227 indicates a small effect. That is, a little association between the groups.

To determine

How would the outcome of hypothesis and Cramer’s V will be written in the report.

Answer to Problem 13P

Report will be ${\chi }^2(2,n=150)=7.77,p<0.05,V=0.16$.

Explanation of Solution

The result showed that the proportion of participants who claim to remember broken glass differ significantly from group to group.

${\chi }^2(2,n=150)=7.77,p<0.05,V=0.16$