
Concept explainers
Doughnuts are cooked by dropping the dough into hot vegetable oil until it changes from white to a rich, golden brown. One popular brand of doughnut automates this process; the doughnuts are made on an assembly line that customers can view in operation as they wait to order. Watching the doughnuts cook gives the customers time to develop an appetite as they ponder the physics of the process.
First, the uncooked doughnut is dropped into hot vegetable oil, whose density is ρ = 919 kg/m3. There it browns on one side as it floats on the oil. After cooking for the proper amount of time, a mechanical lever flips the doughnut over so it can cook on the other side. The doughnut floats fairly high in the oil, with less than half of its volume submerged. As a result, the final product has a characteristic white stripe around the middle where the dough is always out of the oil, as shown in Figure 15-54.
Figure 15-54 Steps in cooking a doughnut

The relationship between the density of the doughnut and the height of the white stripe is graphed in Figure 15-55. On the x axis we plot the density of the doughnut as a fraction of the density of the vegetable cooking oil; the y axis shows the height of the white stripe as a fraction of the total height of the doughnut. Notice that the height of the white stripe is plotted for both positive and negative values.
Figure 15-55 Cooking a floating doughnut
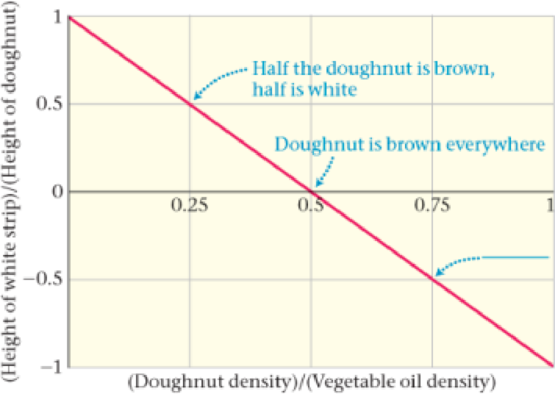
109. •• A new doughnut is being planned whose density will be 330 kg/m3. If the height of the doughnut is H, what will be the height of the white stripe?
- A. 0.14H
- B. 0.24H
- C. 0.28H
- D. 0.64H
Want to see the full answer?
Check out a sample textbook solution
Chapter 15 Solutions
EBK PHYSICS
Additional Science Textbook Solutions
Organic Chemistry (8th Edition)
Introductory Chemistry (6th Edition)
Human Physiology: An Integrated Approach (8th Edition)
Applications and Investigations in Earth Science (9th Edition)
Microbiology: An Introduction
Brock Biology of Microorganisms (15th Edition)
- Please solve and answer this problem correctly please. Thank you!!arrow_forwarda) Use the node-voltage method to find v1, v2, and v3 in the circuit in Fig. P4.14. b) How much power does the 40 V voltage source deliver to the circuit? Figure P4.14 302 202 w w + + + 40 V V1 80 Ω 02 ΣΑΩ 28 A V3 + w w 102 202arrow_forwardPlease solve and answer this problem correctly please. Thank you!!arrow_forward
- You're on an interplanetary mission, in an orbit around the Sun. Suppose you make a maneuver that brings your perihelion in closer to the Sun but leaves your aphelion unchanged. Then you must have Question 2 options: sped up at perihelion sped up at aphelion slowed down at perihelion slowed down at aphelionarrow_forwardThe force of the quadriceps (Fq) and force of the patellar tendon (Fp) is identical (i.e., 1000 N each). In the figure below angle in blue is Θ and the in green is half Θ (i.e., Θ/2). A) Calculate the patellar reaction force (i.e., R resultant vector is the sum of the horizontal component of the quadriceps and patellar tendon force) at the following joint angles: you need to provide a diagram showing the vector and its components for each part. a1) Θ = 160 degrees, a2) Θ = 90 degrees. NOTE: USE ONLY TRIGNOMETRIC FUNCTIONS (SIN/TAN/COS, NO LAW OF COSINES, NO COMPLICATED ALGEBRAIC EQUATIONS OR ANYTHING ELSE, ETC. Question A has 2 parts!arrow_forwardThe force of the quadriceps (Fq) and force of the patellar tendon (Fp) is identical (i.e., 1000 N each). In the figure below angle in blue is Θ and the in green is half Θ (i.e., Θ/2). A) Calculate the patellar reaction force (i.e., R resultant vector is the sum of the horizontal component of the quadriceps and patellar tendon force) at the following joint angles: you need to provide a diagram showing the vector and its components for each part. a1) Θ = 160 degrees, a2) Θ = 90 degrees. NOTE: USE DO NOT USE LAW OF COSINES, NO COMPLICATED ALGEBRAIC EQUATIONS OR ANYTHING ELSE, ETC. Question A has 2 parts!arrow_forward
- No chatgpt pls will upvotearrow_forwardThe force of the quadriceps (Fq) and force of the patellar tendon (Fp) is identical (i.e., 1000 N each). In the figure below angle in blue is Θ and the in green is half Θ (i.e., Θ/2). A) Calculate the patellar reaction force (i.e., R resultant vector is the sum of the horizontal component of the quadriceps and patellar tendon force) at the following joint angles: you need to provide a diagram showing the vector and its components for each part. a1) Θ = 160 degrees, a2) Θ = 90 degrees. NOTE: USE ONLY TRIGNOMETRIC FUNCTIONS (SIN/TAN/COS, NO LAW OF COSINES, NO COMPLICATED ALGEBRAIC EQUATIONS OR ANYTHING ELSE, ETC. Question A has 2 parts!arrow_forwardNo chatgpt pls will upvotearrow_forward
- No chatgpt pls will upvotearrow_forwardSolve and answer the question correctly please. Thank you!!arrow_forward་ The position of a particle is described by r = (300e 0.5t) mm and 0 = (0.3t²) rad, where t is in seconds. Part A Determine the magnitude of the particle's velocity at the instant t = 1.5 s. Express your answer to three significant figures and include the appropriate units. v = Value Submit Request Answer Part B ? Units Determine the magnitude of the particle's acceleration at the instant t = 1.5 s. Express your answer to three significant figures and include the appropriate units. a = Value A ? Unitsarrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





