
To solve: The function is defined on the interval ,
a. Graph .
In (b)–(e), approximate the area under from 0 to 3 as follows:
Answer to Problem 11AYU
a.
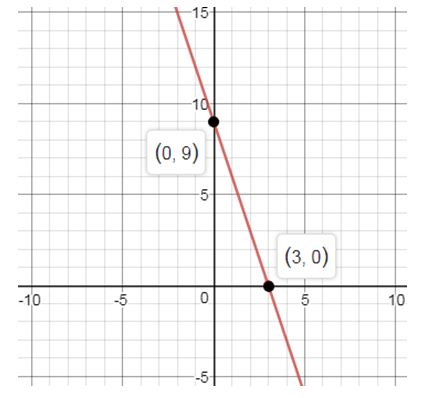
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
a. Graph
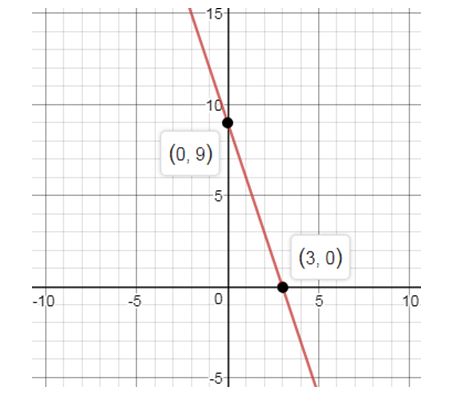
To solve: The function is defined on the interval ,
b. Partition into three subintervals of equal length and choose as the left endpoint of each subinterval.
Answer to Problem 11AYU
b. 18
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
b. Partition into three subintervals of equal length 1 and choose as the left endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
c. Partition into three subintervals of equal length and choose as the right endpoint of each subinterval.
Answer to Problem 11AYU
c. 9
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
c. Partition into three subintervals of equal length 1 and choose as the right endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
d. Partition into six subintervals of equal length and choose as the left endpoint of each subinterval.
Answer to Problem 11AYU
d.
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
d. Partition into six subintervals of equal length and choose as the left endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
e. Partition into six subintervals of equal length and choose as the right endpoint of each subinterval.
Answer to Problem 11AYU
e.
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
e. Partition into six subintervals of equal length and choose as the right endpoint of each subinterval.
The area is approximated as
To solve: The function is defined on the interval ,
f. What is the actual area ?
Answer to Problem 11AYU
f.
Explanation of Solution
Given:
The function is defined on the interval .
Calculation:
f. The actual area under the graph of from 0 to 3 is the area of a right triangle whose base is of length 3 and whose height is 9. The actual area is
Therefore
Chapter 14 Solutions
Precalculus
Additional Math Textbook Solutions
Elementary Statistics
A First Course in Probability (10th Edition)
Pre-Algebra Student Edition
Basic Business Statistics, Student Value Edition
Algebra and Trigonometry (6th Edition)
Elementary Statistics (13th Edition)
- A 20 foot ladder rests on level ground; its head (top) is against a vertical wall. The bottom of the ladder begins by being 12 feet from the wall but begins moving away at the rate of 0.1 feet per second. At what rate is the top of the ladder slipping down the wall? You may use a calculator.arrow_forwardExplain the focus and reasons for establishment of 12.4.1(root test) and 12.4.2(ratio test)arrow_forwarduse Integration by Parts to derive 12.6.1arrow_forward
- Explain the relationship between 12.3.6, (case A of 12.3.6) and 12.3.7arrow_forwardExplain the key points and reasons for the establishment of 12.3.2(integral Test)arrow_forwardUse 12.4.2 to determine whether the infinite series on the right side of equation 12.6.5, 12.6.6 and 12.6.7 converges for every real number x.arrow_forward
- use Corollary 12.6.2 and 12.6.3 to derive 12.6.4,12.6.5, 12.6.6 and 12.6.7arrow_forwardExplain the focus and reasons for establishment of 12.5.1(lim(n->infinite) and sigma of k=0 to n)arrow_forwardExplain the focus and reasons for establishment of 12.5.3 about alternating series. and explain the reason why (sigma k=1 to infinite)(-1)k+1/k = 1/1 - 1/2 + 1/3 - 1/4 + .... converges.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





