Chapter 14, Problem 63CR

a.

To determine

Test whether the linear relationship is useful or not at the 0.01 level of significance.

Answer to Problem 63CR

There is convincing evidence that the linear relationship is useful between y and at least one of the predictors at the 0.01 level of significance.

Explanation of Solution

Calculation:

It is given that variable y is the average language score, $x_1$ is occupational index, $x_2$ is median income, $x_3$ is percentage of title I enrollment, $x_4$ is Hispanic enrollment, $x_5$ is logarithm of fourth-grade enrollment, $x_6$ is prior test score, $x_7$ is administrator teacher ratio, $x_8$ is pupil teacher ratio, $x_9$ is certified staff pupil ratio, and $x_{10},x_{11}$ are the indicator variables for average teaching experience. The sample size is 88 and the number of variables (k) is 11.

1.

The model is $y=\alpha +{\beta }_1{x}_1+{\beta }_2{x}_2+\mathrm{...}+{\beta }_{11}{x}_{11}+e$.

2.

Null hypothesis:

$H_0:{\beta }_1={\beta }_2=\mathrm{...}={\beta }_{11}=0$

That is, there is no useful linear relationship between y and any of the predictors.

3.

Alternative hypothesis:

$H_a:$ At least one among ${\beta }_i^{\text{'}}\text{s}$ is not zero.

That is, there is a useful linear relationship between y and any of the predictors.

4.

Here, the significance level is $\alpha =0.01$.

5.

Test statistic:

$F=\frac{\frac{R^2}{k}}{\frac{\left(1-R^2\right)}{n-\left(k+1\right)}}$

Here, n is the sample size and k is the number of variables in the model.

6.

Assumptions:

Since there is no availability of original data to check the assumptions, there is a need to assume that the variables are related to the model, and the random deviation is distributed normally with mean 0 and the fixed standard deviation.

7.

Calculation:

The value of $R^2$ is 0.64.

The value of F-test statistic is calculated as follows:

$\begin{array}{c}F=\frac{\frac{R^2}{k}}{\frac{\left(1-R^2\right)}{n-\left(k+1\right)}}\\ =\frac{\frac{0.64}{11}}{\frac{\left(1-0.64\right)}{\left(88-\left(11+1\right)\right)}}\\ =\frac{0.058}{\frac{0.36}{76}}\\ =\frac{0.058\times 76}{0.36}\\ =\frac{4.408}{0.36}\\ =12.24\end{array}$

8.

P-value:

Software procedure:

Step-by-step procedure to find the P-value using the MINITAB software:

• Choose Graph > Probability Distribution Plot choose View Probability > OK.
• From Distribution, choose ‘F’ distribution.
• Enter the Numerator df as 11 and Denominator df as 76.
• Click the Shaded Area tab.
• Choose X Value and Right Tail for the region of the curve to shade.
• Enter the X value as 12.24.
• Click OK.

Output obtained using the MINITAB software is represented as follows:

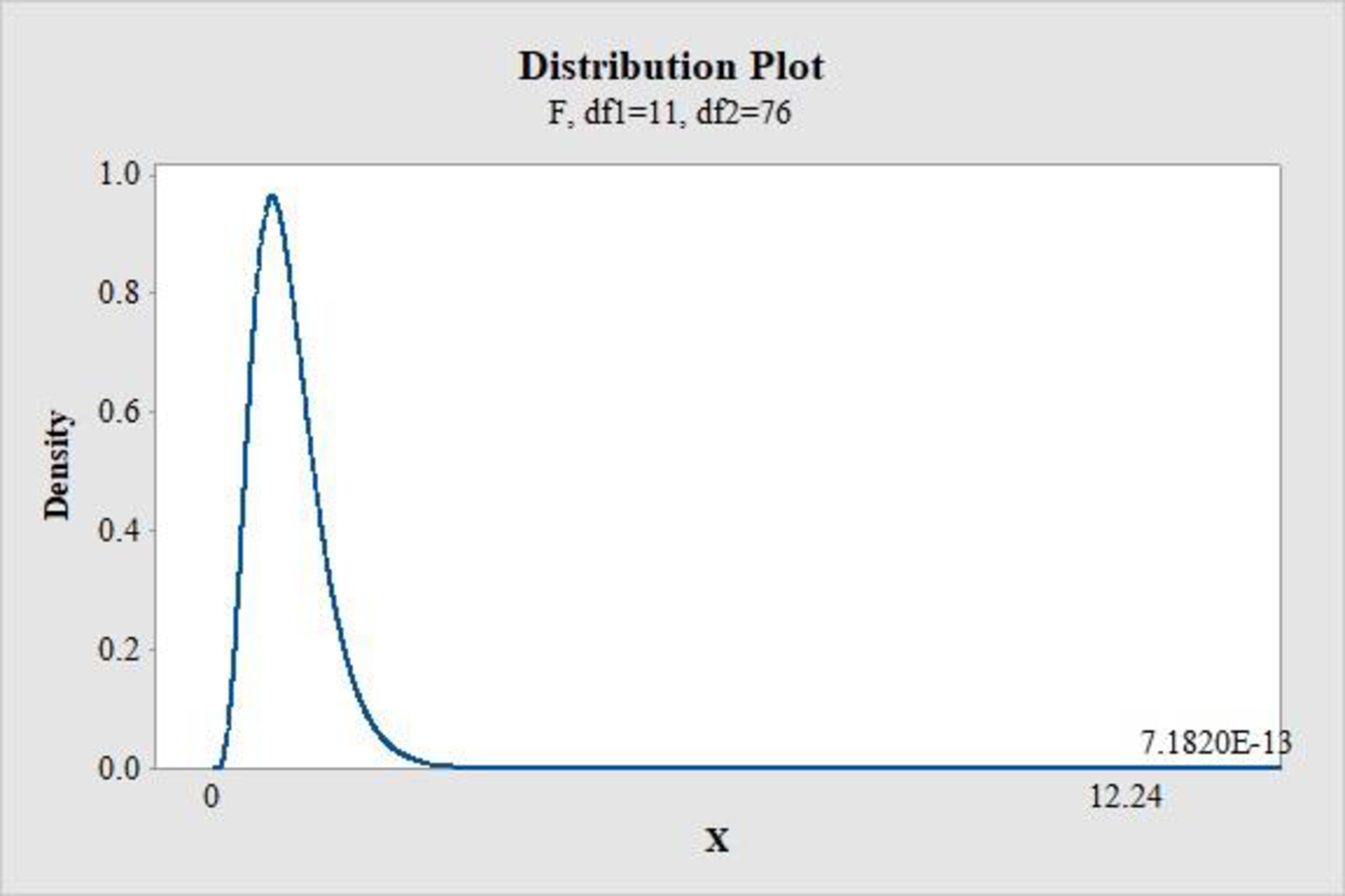
From MINITAB output, the P-value is 0.

9.

Conclusion:

If $P\text{-value}\le \alpha$, then reject the null hypothesis.

Therefore, the P-value of 0 is less than the 0.01 level of significance.

Hence, reject the null hypothesis.

Thus, there is convincing evidence that the linear relationship is useful between y and at least one of the predictors at the 0.01 level of significance.

b.

To determine

Calculate the value of adjusted $R^2$.

Answer to Problem 63CR

The value of adjusted $R^2$ is 0.5879.

Explanation of Solution

Calculation:

The formula for adjusted $R^2$ is as follows:

$R_{adj}^2=1-\left(1-R^2\right)\left(\frac{n-1}{n-\left(k+1\right)}\right)$

Substitute the value of $R^2$ as 0.64, n as 88, and k as 11 in the adjusted $R^2$ formula.

$\begin{array}{c}{R}_{adj}^2=1-\left(1-R^2\right)\left(\frac{n-1}{n-\left(k+1\right)}\right)\\ =1-\left(1-0.64\right)\left(\frac{88-1}{88-\left(11+1\right)}\right)\\ =1-\left(0.36\right)\left(\frac{87}{76}\right)\\ =1-0.4121\\ =0.5879\end{array}$

Thus, the value of adjusted $R^2$ is 0.5879.

c.

To determine

Calculate a 95% confidence interval for ${\beta }_1$ and interpret it.

Answer to Problem 63CR

The 95% confidence interval for ${\beta }_1$ is $\left(\underset{\_}{0.1615,0.7545}\right)$.

Explanation of Solution

Calculation:

Here, ${\beta }_1$ is the coefficient of variable $x_1$.

Since there is no availability of original data to check the assumptions, there is a need to assume that the variables are related to the model, and the random deviation is distributed normally with mean 0 and the fixed standard deviation.

The formula for confidence interval for ${\beta }_1$ is as follows:

$b_1\pm \left(t\text{ critical value}\right)s_{b_1}$.

Where, $b_1$ is the estimated value of ${\beta }_1$ and $s_{b_1}$ is the estimated standard deviation of $b_1$.

Degrees of freedom:

$\begin{array}{c}df=n-\left(k+1\right)\\ =88-\left(11+1\right)\\ =88-12\\ =76\end{array}$

Software procedure:

Step-by-step procedure to find P-value using the MINITAB software:

• Choose Graph > Probability Distribution Plot choose View Probability > OK.
• From Distribution, choose ‘t’ distribution.
• Enter the Degrees of freedom as 76.
• Click the Shaded Area tab.
• Choose Probability and Both Tails for the region of the curve to shade.
• Enter the Probability value as 0.05.
• Click OK.

Output obtained using the MINITAB software is represented as follows:

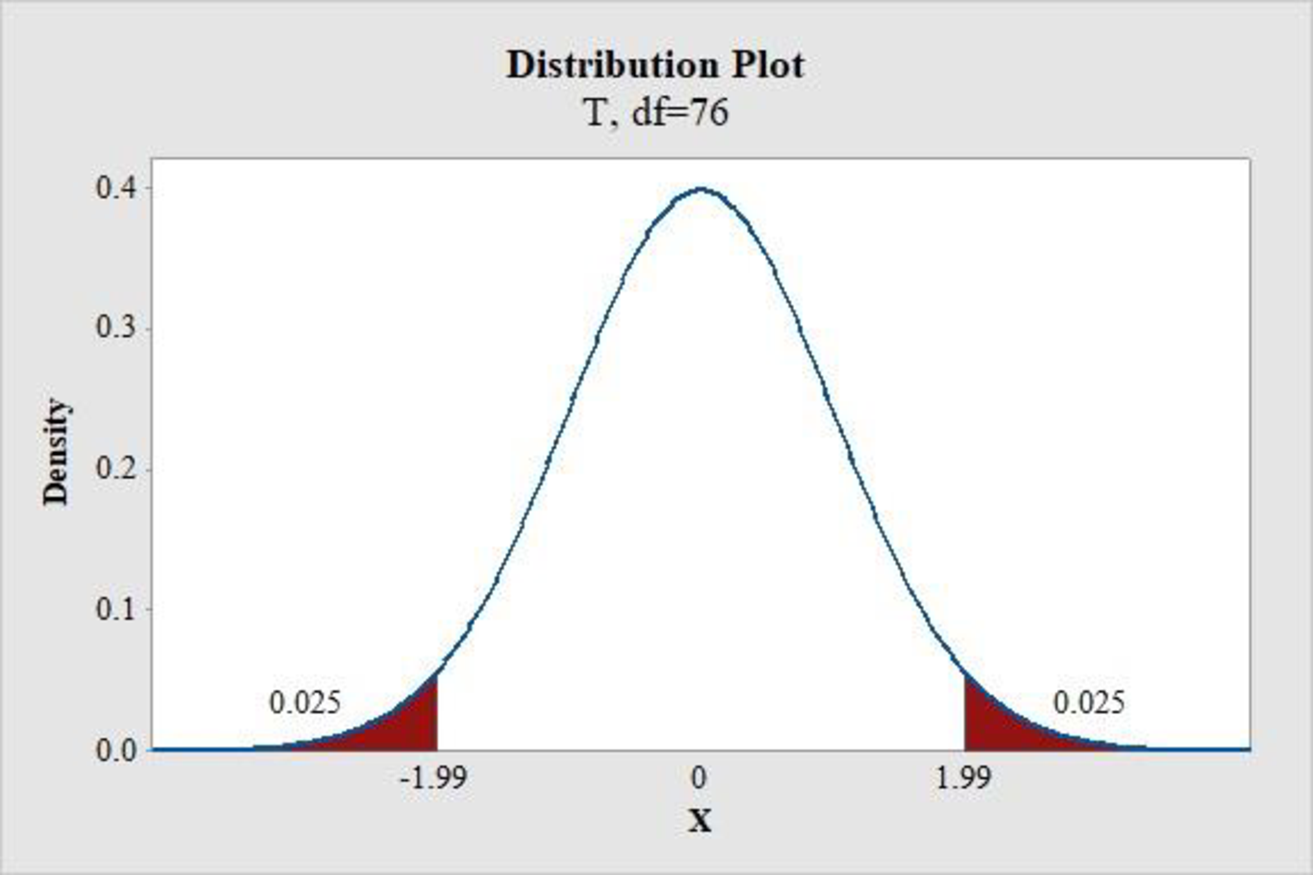
From the MINITAB output, the critical value is 1.99.

The value of $s_{b_1}$ is calculated as follows:

$\begin{array}{c}{s}_{b_1}=\frac{b_1}{t_1}\\ =\frac{0.458}{3.08}\\ =0.149\end{array}$

Here, the value of $b_1$ is 0.458 and the value of $s_{b_1}$ is 0.149.

The 95% confidence interval for ${\beta }_1$ is calculated as follows:

$\begin{array}{c}{b}_1\pm \left(t\text{ critical value}\right)s_{b_1}=0.458\pm \left(1.99\right)0.149\\ =0.458\pm 0.2965\\ =\left(0.458-0.2965,0.458+0.2965\right)\\ =\left(0.1615,0.7545\right)\end{array}$

Thus, the 95% confidence interval for ${\beta }_1$ is $\left(\underset{\_}{0.1615,0.7545}\right)$.

Interpretation:

There is 95% confidence that the average increase in y associated with 1-unit increase in occupational index is between 0.1615 and 0.7545, when the other predictors are fixed.

d.

To determine

Check whether one or more predictors could be eliminated from the model and find which one could be eliminated first.

Answer to Problem 63CR

The variable $\underset{\_}{x_9}$ leads to be eliminated.

Explanation of Solution

Calculation:

The criterion of elimination of a variable is, if t-ratio satisfies $-2\le t\text{ ratio}\le 2$, it can be eliminated from the model.

From the given output in step 1, the t-ratio for $x_1$ is 3.08, the t-ratio for $x_2$ is –0.59, the t-ratio for $x_3$ is –4.02, the t-ratio for $x_4$ is –1.73, the t-ratio for $x_5$ is –2.34, the t-ratio for $x_6$ is 3.60, the t-ratio for $x_7$ is 0.42, the t-ratio for $x_8$ is 0.42, the t-ratio for $x_9$ is –0.27, the t-ratio for $x_{10}$ is –1.30, and the t-ratio for $x_{11}$ is –0.58.

Here, the t-ratio for $x_2$, $x_4$, $x_7$, $x_8$, $x_9$, $x_{10}$, and $x_{11}$ variables are satisfying the criteria of elimination. However, the value of t ratio, which is closest to zero, will be eliminated first. Therefore, the value of –0.27 is close to zero among these variables. Thus, the variable $\underset{\_}{x_9}$ leads to be eliminated.

e.

To determine

Identify the hypothesis that can be tested to identify whether any of the peer group variables provided useful information about y.

Explain if any one of the test procedures presented in the chapter can be used.

Explanation of Solution

Calculation:

Hypotheses:

Null hypothesis:

$H_0:{\beta }_1={\beta }_3={\beta }_9=0$.

Alternative hypothesis:

$H_a:$ At least one among ${\beta }_i^{\text{'}}\text{s}$ is not zero.

There are no procedures presented in this chapter that could be used to test the above hypotheses. In this chapter, the procedures to be tested for the model utility or significance of individual predictors are presented. Moreover, the given null hypothesis is based on the testing of a subset that contains four predictors.