
Concept explainers
Review. For the arrangement shown in Figure P14.60, the inclined plane and the small pulley are frictionless; the string supports the object of mass M at the bottom of the plane; and the string has mass m. The system is in equilibrium, and the vertical part of the string has a length h. We wish to study standing waves set up in the vertical section of the string. (a) What analysis model describes the object of mass M? (b) What analysis model describes the waves on the vertical part of the string? (c) Find the tension in the string. (d) Model the shape of the string as one leg and the hypotenuse of a right triangle. Find the whole length of the string. (e) Find the mass per unit length of the string. (f) Find the speed of waves on the string. (g) Find the lowest frequency for a standing wave on the vertical section of the string. (h) Evaluate this result for M = 1.50 kg, m = 0.750 g, h = 0.500 m, and θ = 30.0°. (i) Find the numerical value for the lowest frequency for a standing wave on the sloped section of the string.
Figure P14.60
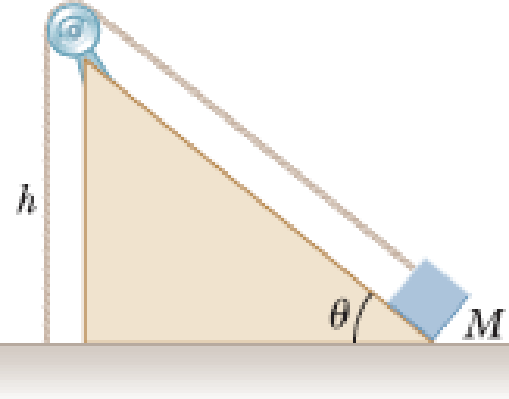
(a)
The analysis model
Answer to Problem 60P
The object is described using constant acceleration model.
Explanation of Solution
The mass of the object supported by the string is
The object of mass
Conclusion:
Therefore, the object of mass
(b)
The analysis model
Answer to Problem 60P
The waves on the vertical part of the string can be described using the waves under boundary conditions model.
Explanation of Solution
The mass of the object supported by the string is
The vertical portion of the string is fixed at both the ends hence the boundary conditions stand for the waves. Write the general equation for the wavelength on the string.
Here,
Conclusion:
Therefore, the waves on the vertical part of the string can be described using the waves under boundary conditions model.
(c)
The tension on the string
Answer to Problem 60P
The tension on the string is
Explanation of Solution
Figure.1 shows the arrangement of the mass-pulley system.
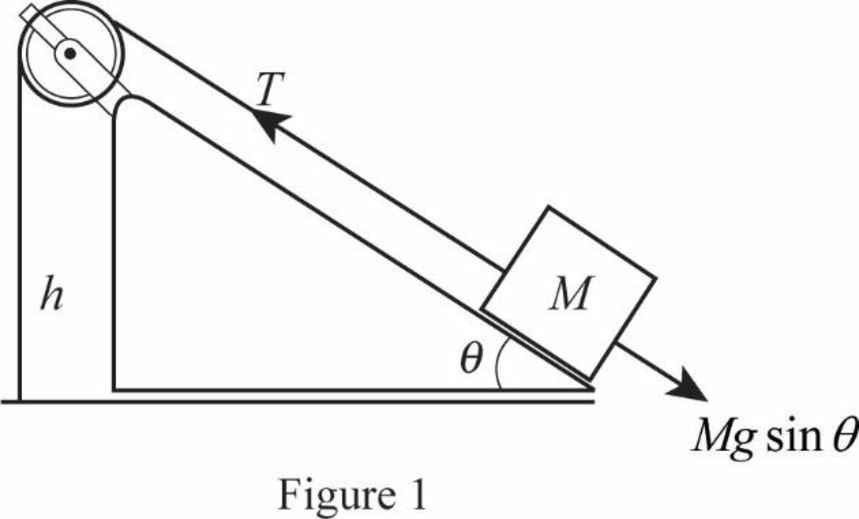
Write the equation for the net force acting on the mass.
Here,
Conclusion:
Re-write the equation (I) such that the net force is zero.
Therefore, the tension on the string is
(d)
The length of the string
Answer to Problem 60P
The length of the string is
Explanation of Solution
Write the equation for the sine of the angle of inclination.
Rewrite the equation (I) to find the equation for the
Write the equation for the total length of the string.
Conclusion:
Substitute equation (II) in equation (III).
Therefore, the length of the strings is
(e)
The mass per unit length of the string
Answer to Problem 60P
The mass per unit length of the string is
Explanation of Solution
Write the equation for the mass per unit length of the string.
Here,
Conclusion:
Substitute equation (V) in equation (VI).
Therefore, the mass per unit length of the string is
(f)
The speed of waves on the string
Answer to Problem 60P
The speed of waves on the string is
Explanation of Solution
Write the equation for the speed of the waves on the string.
Here,
Conclusion:
Substitute equation (II) and equation (VIII) in equation (IX).
Therefore, the speed of the waves on the string is
(g)
The lowest frequency for a standing wave
Answer to Problem 60P
The lowest frequency for the standing waves is
Explanation of Solution
The length
Write the equation for the frequency of the standing wave.
Here,
Conclusion:
Substitute equation (X) and equation (XI) in equation (XII).
Therefore, the lowest possible frequency of the standing waves is
(h)
The lowest frequency for a set of given values
Answer to Problem 60P
The lowest frequency for the standing waves is
Explanation of Solution
Write the equation for the lowest frequency of the standing wave from equation (XIII).
Conclusion:
Substitute
Therefore, the lowest frequency of the standing waves is
(i)
The lowest frequency on the sloped section
Answer to Problem 60P
The lowest frequency for the standing waves on the sloped section is
Explanation of Solution
The wavelength of the fundamental mode of vibration is twice the length of the sloped section.
Here,
Substitute equation (X) and equation (XIV) in equation (XII).
Substitute
Therefore, the lowest frequency of the standing waves is
Want to see more full solutions like this?
Chapter 14 Solutions
Bundle: Principles of Physics: A Calculus-Based Text, 5th + WebAssign Printed Access Card for Serway/Jewett's Principles of Physics: A Calculus-Based Text, 5th Edition, Multi-Term
- No chatgpt pls will upvotearrow_forward1.62 On a training flight, a Figure P1.62 student pilot flies from Lincoln, Nebraska, to Clarinda, Iowa, next to St. Joseph, Missouri, and then to Manhattan, Kansas (Fig. P1.62). The directions are shown relative to north: 0° is north, 90° is east, 180° is south, and 270° is west. Use the method of components to find (a) the distance she has to fly from Manhattan to get back to Lincoln, and (b) the direction (relative to north) she must fly to get there. Illustrate your solutions with a vector diagram. IOWA 147 km Lincoln 85° Clarinda 106 km 167° St. Joseph NEBRASKA Manhattan 166 km 235° S KANSAS MISSOURIarrow_forwardPlz no chatgpt pls will upvotearrow_forward
- 3.19 • Win the Prize. In a carnival booth, you can win a stuffed gi- raffe if you toss a quarter into a small dish. The dish is on a shelf above the point where the quarter leaves your hand and is a horizontal dis- tance of 2.1 m from this point (Fig. E3.19). If you toss the coin with a velocity of 6.4 m/s at an angle of 60° above the horizontal, the coin will land in the dish. Ignore air resistance. (a) What is the height of the shelf above the point where the quarter leaves your hand? (b) What is the vertical component of the velocity of the quarter just before it lands in the dish? Figure E3.19 6.4 m/s 2.1arrow_forwardCan someone help me answer this thank you.arrow_forward1.21 A postal employee drives a delivery truck along the route shown in Fig. E1.21. Determine the magnitude and direction of the resultant displacement by drawing a scale diagram. (See also Exercise 1.28 for a different approach.) Figure E1.21 START 2.6 km 4.0 km 3.1 km STOParrow_forward
- help because i am so lost and it should look something like the picturearrow_forward3.31 A Ferris wheel with radius Figure E3.31 14.0 m is turning about a horizontal axis through its center (Fig. E3.31). The linear speed of a passenger on the rim is constant and equal to 6.00 m/s. What are the magnitude and direction of the passenger's acceleration as she passes through (a) the lowest point in her circular motion and (b) the high- est point in her circular motion? (c) How much time does it take the Ferris wheel to make one revolution?arrow_forward1.56 ⚫. Three horizontal ropes pull on a large stone stuck in the ground, producing the vector forces A, B, and C shown in Fig. P1.56. Find the magnitude and direction of a fourth force on the stone that will make the vector sum of the four forces zero. Figure P1.56 B(80.0 N) 30.0 A (100.0 N) 53.0° C (40.0 N) 30.0°arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





