Mathematics For Machine Technology
8th Edition
ISBN: 9781337798310
Author: Peterson, John.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 14, Problem 50A
In the following table, the radii and heights of cylinders are given. Determine the volumes of the cylinders. Round the answers to the nearest whole number.
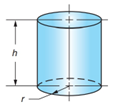
50.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Advanced Functional Analysis Mastery Quiz
Instructions:
.
No partial credit will be awarded; any mistake will result in a score of 0.
Submit your solution before the deadline.
Ensure your solution is detailed, and all steps are well-documented
No Al tools (such as Chat GPT or others) may be used to assist in solving the problems. All work
must be your own.
Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a
score of 0.
Problem
Let X and Y be Banach spaces, and T: XY be a bounded linear operator. Consider the
following tasks
1. [Operator Norm and Boundedness] a. Prove that for any bounded linear operator T: XY
the norm of satisfies:
Tsup ||T(2)||.
2-1
b. Show that if T' is a bounded linear operator on a Banach space and T <1, then the
operatur 1-T is inverüble, and (IT) || ST7
2. [Weak and Strong Convergence] a Define weak and strong convergence in a Banach space .X.
Provide examples of sequences that converge weakly but not strongly, and vice…
please solve handwritten without use of AI
Advanced Mathematics Mastery Quiz
Instructions:
.
No partial credit will be awarded; any mistake will result in a score of 0.
. Submit your solution before the deadline.
•
Ensure your solution is detailed, and all steps are well-documented.
.
No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work
must be your own.
Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a
score of 0.
Problem
Let the function f(x, y, z) = r³y-2xy + 3yz² +e+y+ and consider the following tasks:
1. [Critical Points and Classification] a. Find all critical points of f(x, y, z).
b. Use the second partial derivative test to classify each critical point as a local minimum, local
maximum, or saddle point.
2. [Gradient and Divergence] a. Compute the gradient vector Vf.
b. Calculate the divergence of the gradient field and explain its significance.
3. [Line Integral Evaluation] Consider the vector field F(x, y, z) = (e² + yz, x²y
ar).
a.…
Chapter 14 Solutions
Mathematics For Machine Technology
Ch. 14 - Subtract 7516278 .Ch. 14 - Multiply 7238 . Express the result as a mixed...Ch. 14 - Multiply 1.7022.35 .Ch. 14 - Use Figure 14-5 to answer Exercises 4 through 6....Ch. 14 - Use Figure 14-5 to answer Exercises 4 through 6....Ch. 14 - Use Figure 14-5 to answer Exercises 4 through 6....Ch. 14 - Raise the following numbers to the indicated...Ch. 14 - Raise the following numbers to the indicated...Ch. 14 - Raise the following numbers to the indicated...Ch. 14 - Raise the following numbers to the indicated...
Ch. 14 - Raise the following numbers to the indicated...Ch. 14 - Raise the following numbers to the indicated...Ch. 14 - Raise the following numbers to the indicated...Ch. 14 - Raise the following numbers to the indicated...Ch. 14 - Raise the following numbers to the indicated...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the lengths of the sides...Ch. 14 - In the following table, the radii of circles are...Ch. 14 - In the following table, the radii of circles are...Ch. 14 - In the following table, the radii of circles are...Ch. 14 - In the following table, the radii of circles are...Ch. 14 - In the following table, the radii of circles are...Ch. 14 - In the following table, the diameters of spheres...Ch. 14 - In the following table, the diameters of spheres...Ch. 14 - In the following table, the diameters of spheres...Ch. 14 - In the following table, the diameters of spheres...Ch. 14 - In the following table, the diameters of spheres...Ch. 14 - In the following table, the radii and heights of...Ch. 14 - In the following table, the radii and heights of...Ch. 14 - In the following table, the radii and heights of...Ch. 14 - In the following table, the radii and heights of...Ch. 14 - In the following table, the radii and heights of...Ch. 14 - In the following table, the diameters and heights...Ch. 14 - In the following table, the diameters and heights...Ch. 14 - In the following table, the diameters and heights...Ch. 14 - In the following table, the diameters and heights...Ch. 14 - Prob. 55ACh. 14 - Prob. 56ACh. 14 - Prob. 57ACh. 14 - Find the area of this plate. All dimensions are in...Ch. 14 - Find the metal volume of this bushing. All...Ch. 14 - Find the volume of this pin. All dimensions are in...Ch. 14 - Prob. 61A
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.Similar questions
- Advanced Functional Analysis Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. ⚫ Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. • No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X te a Banach space, and let T: XX be a linear operetor satisfying ||T|| - 1. Corsider the following tasks: 1. [Bounded Linear Operators] a. Prove that I is a bounded linear operator if and only if there exists a constant C such that ||T()||C|||| for all 2 € X. b. Show that if I' is a linear operator on a Banach space X and ||T||-1, then ||T(x)||||||| for all EX. 2. [Spectral Theorem] Let A be a self-adjoint operator on a Hibert space H. Assume that A has a non-empty spectrum. a. State and prove the Spectral…arrow_forwardAdvanced Mathematics Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. . . No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let the function f(x, y, z)=-42y+2ay" +22 tasks: and consider the following 1. [Critical Points and Classification] a. Find all critical points of f(x, y, z). b. Use the second partial derivative test to classify each critical point as a local minimum, local maximum, or saddle point. 2. [Directional Derivatives and Gradients] a. Compute the gradient vector Vf of f(x, y, z). b. Find the directional derivative of f at the point (1, 1, 1) in the direction of the vector v = (1,-2,3). 3. [Line Integral Evaluation] Consider the…arrow_forwardAdvanced Functional Analysis Mastery Quiz Instructions: . . No partial credit will be awarded; any mistake will result in a score of 0. Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. . . No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X and Y be Banach spaces, and let T: XY be a bounded linear operator. Consider the following tasks: 1. [Baire's Category Theorem and Applications] a. State and prove Baire's Category Theorem for Banach spaces. Use the theorem to prove that a complete metric space cannot be the countable union of nowhere dense sets. b. Use Baire's Category Theorem to show that if T: XY is a bounded linear operator between Banach spaces, then the set of points in X where I' is continuous is a dense G8 set. 2. [Norms and…arrow_forward
- Advanced Functional Analysis Mastery Quiz Instructions: No partial credit will be awarded; any mistake will result in a score of 0. . Submit your solution before the deadline. . Ensure your solution is detailed, and all steps are well-documented. No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X be a Banach space, and 7' be a bounded linear operator acting on X. Consider the following tasks: 1. [Operator Norm and Boundedness] a. Prove that the operator norm of a linear operator T': X →→ X is given by: ||T|| =sup ||T(2)|| 2-1 b. Show that if 'T' is a bounded linear operator on a Banach space, then the sequence {7"} converges to zero pointwise on any bounded subset of X if and only if ||T|| p, from X to X, where 4, (y)=(x, y), is a linear operator. b. Consider a sequence {} CX. Prove that if →→ 6(2)→→ (2)…arrow_forwardMathematics Challenge Quiz Instructions: • You must submit your solution before the deadline. • Any mistake will result in a score of 0 for this quiz. • Partial credit is not allowed; ensure your answer is complete and accurate. Problem Consider the parametric equations: x(t) = e cos(3t), y(t) = e sin(3t) fort Є R. 1. [Parametric Curve Analysis] a. Prove that the parametric curve represents a spiral by eliminating t and deriving the general equation in Cartesian form. b. Find the curvature (t) of the curve at any point 1. 2. [Integral Evaluation] For the region enclosed by the spiral between t = 0 and t =π, compute the area using the formula: where t₁ = 0 and t₂ = . A == √ √ ²x²(1)y (t) − y(t) x' (t)] dt 3. [Differential Equation Application] The curve satisfies a differential equation of the form: d'y da2 dy + P(x)+q(x)y = 0 a. Derive the explicit forms of p(x) and q(2). b. Verify your solution by substituting (t) and y(t) into the differential equation. 4. [Optimization and Limits]…arrow_forwardAdvanced Functional Analysis Mastery Quiz Instructions: No partial credit will be awarded: any mistake will result in a score of 0. Submit your solution before the deadline. Ensure your solution is detailed, and all stops are well-documented. No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X and Y be Banach spaces, and let T: X →Y be a bounded linear operator. Consider the following tasks: 1. [Banach Fixed-Point Theorem] a State and prove the Banach Fixed-Point Theorem (Contraction Mapping Theorem). Provide a detailed explanation of how the theorem guarantees the existence of a unique fixed point for a contraction mapping on a complete metric space. b. Let T: X → X be a contraction mapping on X = R² with T(r. u) = (3.). Find the unique fixed point of T. 2. [Duality and the Hahn-Banach Theorem] a. State…arrow_forward
- Mathematics Mastery Quiz Instructions: • No partial credit will be awarded; any mistake will result in a score of 0. Submit your solution before the deadline. Ensure your solution is detailed and all steps are well-documented. Problem Let the function f(x, y) = x²y³ - 3x+y+ety and consider the following tasks: 1. [Critical Points and Classification] a. Find all critical points of f(x, y). b. Use the second partial derivative test to classify each critical point as a local minimum, local maximum, or saddle point. 2. [Line Integral Evaluation] Consider the vector field F(x, y) = (2x³y - y³ + e², 3x²y² - 4x³ + e³). a. Verify whether F is conservative. b. If conservative, compute the line integral of F along the curve C, parameterized as: C: Sx(t) = t² [y(t) = ln(t + 1)' tЄ [0,1].arrow_forwardAdvanced Functional Analysis Mastery Quiz Instructions: . No partial credit will be awarded; any mistake will result in a score of 0. . Submit your solution before the deadline. Ensure your solution is detailed, and all steps are well-documented. No Al tools (such as ChatGPT or others) may be used to assist in solving the problems. All work must be your own. Solutions will be checked for Al usage and plagiarism. Any detected violation will result in a score of 0. Problem Let X and Y be Banach spaces, and T: XY a bounded linear operator. Consider the following tasks: 1. [Bounded Linear Operators and Closed Graph Theorem] a. State and prove the Closed Graph Theorem, which asserts that if T: XY is a linear operator between Banach spaces and the graph of T' is closed in X x Y, then I' is bounded. b. Using the Closed Graph Theorem, show that if T: XY is an injective linear operator and the graph of 'I' is closed, then I' is bounded. 2. [Convergence and Strong vs Weak Topologies] a. Define…arrow_forwardPlease give a handwritten solution without use of AIarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
The surface area and volume of cone, cylinder, prism and pyramid; Author: AtHome Tuition;https://www.youtube.com/watch?v=SlaQmaJCOt8;License: Standard YouTube License, CC-BY