
The following gas-phase reaction was studied at
Determine the order of the reaction and the rate constant based on the following data.
Time (s) |
P(mmHg) |
0 |
15.76 |
181 |
18.88 |
513 |
22.79 |
1164 |
27.08 |
where P is the total pressure. |
Interpretation:
The order of the reaction and the rate constant, based on the given data, areto be determined.
Concept introduction:
The power of the concentration of reactants is called the order of the reaction.
According to the Arrheniusequation, the rate that is dependent on a given temperature is called the rate constant.
Answer to Problem 22QP
Solution: The order of the reaction is first order and the rate constant is
Explanation of Solution
Given information: The following gas phase reaction was studied at a temperature of
The reaction is as follows:
The given data is as follows:
Consider
The reaction is as follows:
The pressure data is represented below.
Therefore, the pressure increases, and the change in pressure (
The data is represented as follows:
The plot of
The plot of
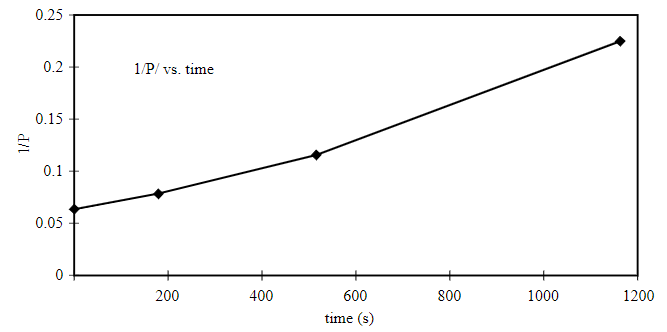
The plot of
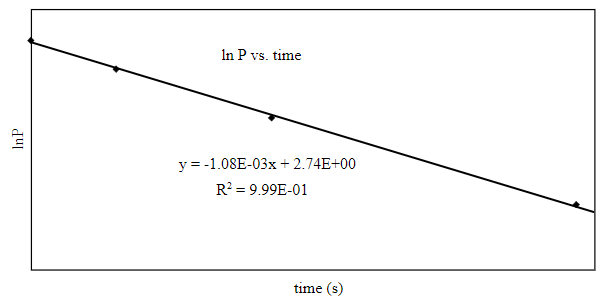
The rate constant for the first-order reaction is as follows:
The reaction is a first-order reaction, as can be interpreted from the graph. The slope for a first-order reaction is equal to the rate constant
The order of reaction is first order and rate constant is
Want to see more full solutions like this?
Chapter 14 Solutions
Chemistry
- Draw the mechanism for the formation of diol by starting with one pen and all in... basic conditions then acidic conditions then draw the mechanism for the formation of a carboxylic acid from your product.arrow_forwardDraw the mechanism for the oxidation of 3-bromo-cyclohexan-1-ol.arrow_forwardConvert the following Fischer projection to Haworth projections. show work and show the arrows please.arrow_forward
- Draw the mechanism for the substitution reaction converting an alcohol into an alkyl halide. If chirality is important to the reaction include it.arrow_forwardWrite, in words three different reactions we can use to make an alcohol.arrow_forwardDraw the reduction mechanism for the reduction of the aldehyde.arrow_forward
 Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning
Chemistry: The Molecular ScienceChemistryISBN:9781285199047Author:John W. Moore, Conrad L. StanitskiPublisher:Cengage Learning Chemistry for Engineering StudentsChemistryISBN:9781285199023Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781285199023Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning





