
(a)
Interpretation:
The number of nodal planes perpendicular to the bonding axes of each of the three
Concept introduction:
Overlap of atomic orbitals (AOs) can be thought of as wave interference. It can be constructive or destructive. Constructive interference increases the electron density between two nuclei (an antinode) and results in a molecular orbital (MO) of lower energy. The phases of overlapping orbitals are the same in this case. Destructive interference decreases the electron density between two nuclei and results in an MO of higher energy. The phases of such AOs are the opposite. Since the electron density between two nuclei decreases, there is a node (or a nodal plane) between the two atoms.
Answer to Problem 14.26P
The number of nodal planes is three for MO A, two for MO B, and four for MO C.
The order of increasing energy of the three MOs is
Explanation of Solution
The phases of the wave function of the two AOs on either side of a nodal plane are opposite each other. This results in destructive interference reducing the electron density to zero at the nodal plane.
Therefore, the nodal planes in the three MOs are:
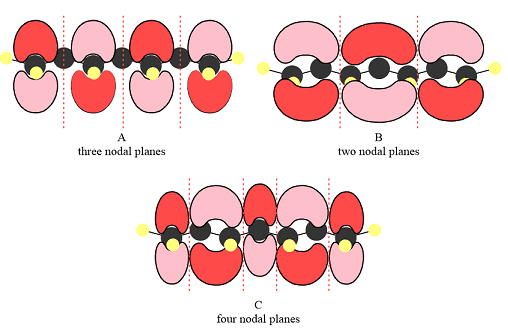
The energy of the MO increases with the number of nodes. Therefore, the order of increasing energy of the three orbitals is
When atomic orbitals with different phases overlap, a node (zero electron density) is formed at the center, increasing the energy of the MO.
(b)
Interpretation:
The p orbital AO contributions on each carbon atom that would give rise to each MO are to be drawn.
Concept introduction:
The p orbitals that contribute to
Answer to Problem 14.26P
The p orbitals that contribute to each of the three MOs are
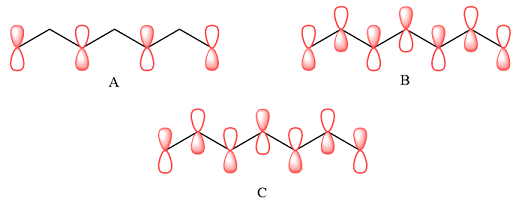
Explanation of Solution
In case of A, the MOs shown are present on alternate carbon atoms. This means they do not overlap and are non-bonding MOs. The corresponding AOs are p orbital on alternate carbon atoms. There is no contribution from atoms that lie in the nodal planes. The p orbitals on either side of each nodal plane have opposite phases.
Therefore, the p orbitals that contribute to MOs shown in A are
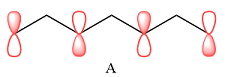
There are no bonding or antibonding interactions in this case.
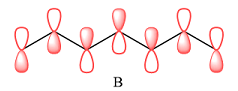
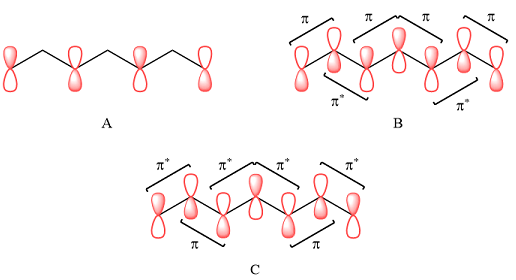
In case of B, there are three bonding MOs. The p orbitals of C1 and C2 (from left) overlap to produce a bonding MO, therefore, they must be in phase. The p orbitals of C3, C4, and C5 overlap constructively to produce a three-center bonding MO. The p orbitals of C6 and C7 overlap to produce another bonding MO. There are two nodal planes, one between C2 and C3, and the second between C5 and C6. This means that the phases of the MOs, and therefore of the contributing AOs on the two sides of each nodal plane must be opposite.
Therefore, the p orbitals contributing to the MOs as shown in B are
In case of C, there are three nodal planes, between C1-C2, between C3-C4, between C4-C5, and between C6-C7. The phases of the orbitals on either side of each nodal plane must be opposite. There are only two bonding MO interactions, the first between C2 and C3 and the second between C5 and C6, therefore, these pairs must be of the same phase.
Therefore, p orbitals contributing to the MOs as shown in C are
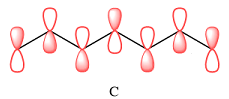
The p orbitals contributing to each MO are determined on the basis of the phases and the presence of an adjacent nodal plane.
(c)
Interpretation:
Each internuclear region is to be identified as having a bonding or an antibonding type of interaction.
Concept introduction:
A bonding interaction arises when the phases of the interacting AOs are the same. This increases the electron density between the two nuclei and lowers the energy of the MO. An antibonding interaction arises when the phases of the interacting AOs are different. This decreases the electron density between the two nuclei to zero at the center and increases the energy of the MO.
Answer to Problem 14.26P
The bonding (
Explanation of Solution
A bonding interaction requires p orbitals of the same phase on adjacent atoms. An antibonding interaction requires the interacting p orbitals to be of opposite phases. An antibonding interaction leads to a nodal plane between the two atoms.
Therefore, in A, there are no bonding or antibonding interactions as the AOs are not on adjacent carbon atoms. In case of B, there are bonding interactions between p AOs of C1 and C2 (from left), between C3, C4, and C5, and between C6 and C7. There are antibonding interactions between C2 and C3 and between C5 and C6.
In case of C, there are two bonding interactions, between C2 and C3, and between C5 and C6. The remaining four interactions are antibonding.

The type of interaction is determined on the basis of the phases of the interacting AOs.
(d)
Interpretation:
Whether each MO is overall bonding, nonbonding or antibonding is to be determined on the basis of the answer to part (c).
Concept introduction:
If the number of bonding interactions are more than the number of antibonding interactions, the MO is overall bonding. If the number of antibonding interactions is more than that of bonding interactions, the MO is overall antibonding. If the numbers are equal or there are no interactions, the MO is overall nonbonding.
Answer to Problem 14.26P
The MO shown in A is overall nonbonding. MO B is overall bonding. MO C is overall antibonding.
Explanation of Solution
The contributing p AOs are on alternate carbon atoms, and therefore, not in a position to interact. Therefore, there are no bonding or antibonding interactions in this case. Therefore, the MO shown in A is overall nonbonding.
In case of B, there are four bonding and two antibonding interactions. Effectively, this means the MO is overall bonding.
In case of C, there are only two bonding interactions but four antibonding interations. Therefore, this MO is overall antibonding.
The overall character of a multicenter MO is determined by the numbers of bonding and antibonding interactions.
Want to see more full solutions like this?
Chapter 14 Solutions
Organic Chemistry: Principles and Mechanisms (Second Edition)
- Explain the term “inductively coupled plasma.”arrow_forwardUsing Pauling electronegativity values and a Ketelaar triangle, what type of compound is brass, a CuZn alloy? Group of answer choices metallic ionic covalentarrow_forwardChallenging samples: 1. Metal complexes with low volatility are often difficult to analyze when performing atomic absorption measurements because the atomization efficiency is reduced to unacceptably low levels. Devise a strategy or strategies for eliminating the problem of a non-volatile metal complex? Explain how you would do that. 2. Devise a strategy to overcome unwanted ionization of the analyte? Explain what it would be. 3. Devise a general method that can be used to account for the presence of unknown matrix effects.arrow_forward
- Don't used hand raitingarrow_forwardDon't used hand raiting don't used Ai solutionarrow_forwardHomework: Atomic Structure This homework is due at the beginning of class next lecture period and is worth 6 points. Please place the number of protons and neutrons in the nucleus and then put the number of electrons in the correct shell. Also give the correct atomic mass. Also, state if the atom is an ion (cation or anion). H* 1. Number of protons Number of electrons Number of neutrons Atomic mass 2. 26 13AI +++ Number of protons Number of neutrons Number of electrons Atomic massarrow_forward
- Don't used Ai solution and don't used hand raitingarrow_forward& Calculate the molar enthalpy of combustion (A combH) of 1.80 g of pyruvic acid (CH3COCOOH; 88.1 g mol-1) at 37 °C when they are combusted in a calorimeter at constant volume with a calorimeter constant = 1.62 kJ °C-1 and the temperature rose by 1.55 °C. Given: R = 8.314 J mol −1 °C-1 and the combustion reaction: AN C3H4O3 + 2.502(g) → 3CO2(g) + 2H2O(l)arrow_forwardAn unknown salt, AB, has the following precipitation reaction:A+(aq) + B-(aq) ⇌ AB(s) the K value for this reaction is 4.50 x10-6. Draw a model that represents what will happen when 1.00 L each of 1.00 M solution of A+(aq) and 1.00M solution of B-(aq) are combined.arrow_forward
 Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning Organic Chemistry: A Guided InquiryChemistryISBN:9780618974122Author:Andrei StraumanisPublisher:Cengage Learning
Organic Chemistry: A Guided InquiryChemistryISBN:9780618974122Author:Andrei StraumanisPublisher:Cengage Learning

