Chapter 13.7, Problem 61E

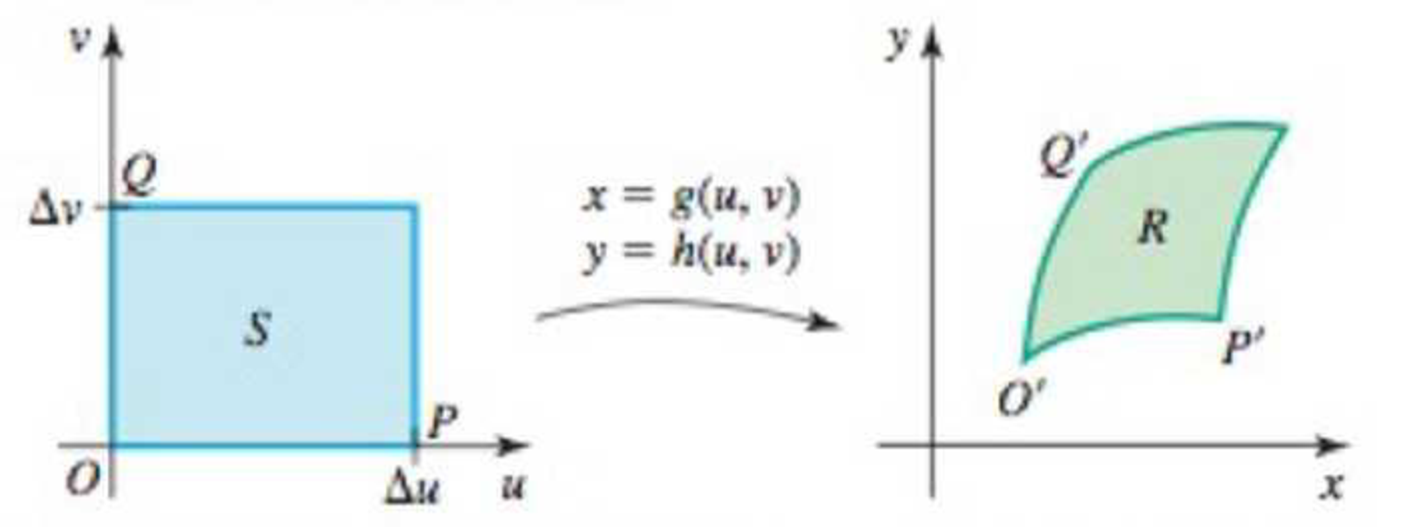
Meaning of the Jacobian The Jacobian is a magnification (or reduction) factor that relates the area of a small region near the point (u, v) to the area of the image of that region near the point (x,y).

a.    Suppose S is a rectangle in the uv-plane with vertices O(0,0), P(Δu, 0), {Δu, Δv), and Q(0, Δv) (see figure). The image of S under the transformation x = g(u, v), y = h(u, v) is a region R in the xy-plane. Let O’ P’ and Q^’ be the images of O, P, and Q, respectively, in the xy-plane, where O’ P’ and Q’ do not all lie on the same line. Explain why the coordinates of O’, P’, and Q’ are (g(0, 0), h(0, 0)), (g(Δu, 0), h(Δu, 0)), and (g(0, Δv), h(0, Δv)), respectively.

 b.    Use a Taylor series in both variables to show that

     $\begin{array}{c}g\left(\Delta u,0\right)\approx g\left(0,0\right)+g_u\left(0,0\right)\Delta u\\ g\left(0,\Delta v\right)\approx g\left(0,0\right)+g_v\left(0,0\right)\Delta v\\ h\left(\Delta u,0\right)\approx h\left(0,0\right)+h_u\left(0,0\right)\Delta u\\ h\left(0,\Delta v\right)\approx h\left(0,0\right)+h_v\left(0,0\right)\Delta v\end{array}$

where g_u (0,0) is $\frac{\partial x}{\partial u}$ evaluated at (0,0), with similar meanings for g_v, h_u, and h_v.

c.    Consider the vectors $\stackrel{\rightharpoonup }{O^{\prime }{P}^{\prime }}$ and $\stackrel{\rightharpoonup }{O^{\prime }{Q}^{\prime }}$ and the parallelogram, two of whose sides are $\stackrel{\rightharpoonup }{O^{\prime }{P}^{\prime }}$ and $\stackrel{\rightharpoonup }{O^{\prime }{Q}^{\prime }}$’. Use the cross product to show that the area of the parallelogram is approximately $\left|J\left(u,v\right)\right|\Delta u\Delta v$.

d.    Explain why the ratio of the area of R to the area of S is approximately |J(u, v)|.