CALCULUS:EARLY TRANSCENDENTALS-PACKAGE
CALCULUS:EARLY TRANSCENDENTALS-PACKAGE
3rd Edition
ISBN: 9780135182543
Author: Briggs
Publisher: PEARSON
bartleby

Concept explainers

Magnitude
A vector is an element with both direction and magnitude. A vector is represented using an arrow, where the arrow represents the direction of the vector and its length is represented using the magnitude. The set of vectors in space is known as vector spa…
bartleby

Videos

Textbook Question
Book Icon
Chapter 13.4, Problem 65E

Scalar triple product Another operation with vectors is the scalar triple product, defined to be u ∙ (v × w), for nonzero vectors u, v, and win ℝ3.

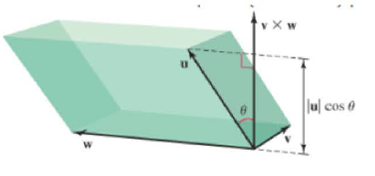
65. Explain why the position vectors u, v, and w are coplanar if and only if |u ∙ (v × w)| = 0. (Hint: See Exercise 63).

63. Consider the parallelepiped (slanted box) determined by the position vectors u, v, and w (see figure). Show that the volume of the parallelepiped is |u ∙ (v × w) |, the absolute value of the scalar triple product.

Chapter 13.4, Problem 65E, Scalar triple product Another operation with vectors is the scalar triple product, defined to be u

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 13.4, Problem 64E
Next
Chapter 13.4, Problem 66E
Students have asked these similar questions
The function f is shown below. If g is an antiderivative of f such that g(6) = 2, what is the maximum value of g on the closed interval [-9,9]? 8 7 6 Сл 5 4 3 1 y Graph of f -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 23 4 -1 -2 -3 -4 -6 56 -5 -7 -8 LO 5 9 7 8 9 10
x The function of is shown below. If I is the function defined by g(x) = [* f(t)dt, write the equation of the line tangent to the graph of 9 at x = -3. g y Graph of f 8 7 6 5 4 32 1 x -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 10 -1 -2 -3 56 -6 -7 -8
Let f(x)=4excosxf'(x)=

Chapter 13 Solutions

CALCULUS:EARLY TRANSCENDENTALS-PACKAGE

Ch. 13.1 - Describe the length and direction of the vector 5v...Ch. 13.1 - Prob. 2QCCh. 13.1 - Prob. 3QCCh. 13.1 - Given the points P(2.3) and Q(4, 1), find the...Ch. 13.1 - Find vectors of length 10 parallel to the unit...Ch. 13.1 - Verify that the vector 513,1213 has length 1.Ch. 13.1 - Solve 3u | 4v = 12w for u.Ch. 13.1 - Interpret the following statement: Points have a...Ch. 13.1 - What is a position vector?Ch. 13.1 - Given a position vector v, why are there...
Ch. 13.1 - Use the points P(3.1) and Q(7.1) to find position...Ch. 13.1 - If u = u1, u2 and v = v1, v2, how do you find u +...Ch. 13.1 - Find two unit vectors parallel to 2,3.Ch. 13.1 - Is 1,1 a unit vector? Explain.Ch. 13.1 - Evaluate 3,1+2,4 and illustrate the sum...Ch. 13.1 - Prob. 9ECh. 13.1 - Express the vector v = v1, v2 in terms of the unit...Ch. 13.1 - How do you compute |PQ| from the coordinates of...Ch. 13.1 - The velocity of a kayak on a lake is v=2,2,22....Ch. 13.1 - Vector operations Refer to the figure and carry...Ch. 13.1 - Vector operations Refer to the figure and carry...Ch. 13.1 - Vector operations Refer to the figure and carry...Ch. 13.1 - Vector operations Refer to the figure and carry...Ch. 13.1 - Prob. 17ECh. 13.1 - Vector operations Refer to the figure and carry...Ch. 13.1 - Components and magnitudes Define the points O(0,...Ch. 13.1 - Prob. 20ECh. 13.1 - Components and equality Define the points P(3, 1),...Ch. 13.1 - Components and equality Define the points P(3, 1),...Ch. 13.1 - Components and equality Define the points P(3, 1),...Ch. 13.1 - Vector operations Let u = 4, 2, v = 4, 6, and w =...Ch. 13.1 - Vector operations Let u = 4, 2, v = 4, 6, and w =...Ch. 13.1 - Vector operations Let u = 4, 2, v = 4, 6, and w =...Ch. 13.1 - Vector operations Let u = 4, 2, v = 4, 6, and w =...Ch. 13.1 - Vector operations Let u = 3, 4, v = 1, 1, and w =...Ch. 13.1 - Vector operations Let u = 3, 4, v = 1, 1, and w =...Ch. 13.1 - Prob. 30ECh. 13.1 - Vector operations Let u = 3, 4, v = 1, 1, and w =...Ch. 13.1 - Find a unit vector in the direction of v = 6,8.Ch. 13.1 - Prob. 33ECh. 13.1 - Prob. 34ECh. 13.1 - Find the vector v of length 6 that has the same...Ch. 13.1 - Find the vector v that has a magnitude of 10 and a...Ch. 13.1 - Designer vectors Find the following vectors. 73....Ch. 13.1 - Prob. 38ECh. 13.1 - How do you find a vector of length 10 in the...Ch. 13.1 - Let v = 8,15. a. Find a vector in the direction of...Ch. 13.1 - Prob. 41ECh. 13.1 - Prob. 42ECh. 13.1 - Unit vectors Define the points P(4, 1), Q(3, 4),...Ch. 13.1 - Prob. 44ECh. 13.1 - Prob. 45ECh. 13.1 - Prob. 46ECh. 13.1 - Unit vectors a. Find two unit vectors parallel to...Ch. 13.1 - Vectors from polar coordinates Suppose O is the...Ch. 13.1 - Vectors from polar coordinates Find the position...Ch. 13.1 - Prob. 50ECh. 13.1 - Find the velocity v of an ocean freighter that is...Ch. 13.1 - Prob. 52ECh. 13.1 - Airplanes and crosswinds Assume each plane flies...Ch. 13.1 - Prob. 54ECh. 13.1 - Airplanes and crosswinds Assume each plane flies...Ch. 13.1 - A boat in a current The water in a river moves...Ch. 13.1 - Another boat in a current The water in a river...Ch. 13.1 - Prob. 58ECh. 13.1 - Boat in a wind A sailboat floats in a current that...Ch. 13.1 - Prob. 60ECh. 13.1 - Prob. 61ECh. 13.1 - Prob. 62ECh. 13.1 - Prob. 63ECh. 13.1 - Prob. 64ECh. 13.1 - Explain why or why not Determine whether the...Ch. 13.1 - Equal vectors For the points A(3, 4), B(6, 10),...Ch. 13.1 - Vector equations Use the properties of vectors to...Ch. 13.1 - Vector equations Use the properties of vectors to...Ch. 13.1 - Prob. 69ECh. 13.1 - Solving vector equations Solve the following pairs...Ch. 13.1 - Prob. 71ECh. 13.1 - Prob. 72ECh. 13.1 - Prob. 73ECh. 13.1 - Ant on a page An ant walks due east at a constant...Ch. 13.1 - Clock vectors Consider the 12 vectors that have...Ch. 13.1 - Three-way tug-of-war Three people located at A, B,...Ch. 13.1 - Additional Exercises 8185. Vector properties Prove...Ch. 13.1 - Additional Exercises 8185. Vector properties Prove...Ch. 13.1 - Vector properties Prove the following vector...Ch. 13.1 - Vector properties Prove the following vector...Ch. 13.1 - Vector properties Prove the following vector...Ch. 13.1 - Prob. 82ECh. 13.1 - Magnitude of scalar multiple Prove that |cv| = |c|...Ch. 13.1 - Equality of vectors Assume PQ equals RS. Does it...Ch. 13.1 - Linear independence A pair of nonzero vectors in...Ch. 13.1 - Perpendicular vectors Show that two nonzero...Ch. 13.1 - Parallel and perpendicular vectors Let u = a, 5...Ch. 13.1 - The Triangle Inequality Suppose u and v are...Ch. 13.2 - Suppose the positive x-, y-, and z-axes point...Ch. 13.2 - To which coordinate planes are the planes x = 2...Ch. 13.2 - Describe the solution set of the equation (x 1)2...Ch. 13.2 - Which of the following vectors are parallel to...Ch. 13.2 - Which vector has the smaller magnitude: u = 3i j ...Ch. 13.2 - Explain how to plot the point (3, 2, 1) in 3.Ch. 13.2 - What is the y-coordinate of all points in the...Ch. 13.2 - Describe the plane x = 4.Ch. 13.2 - Prob. 4ECh. 13.2 - Let u = 3, 5, 7 and v = 6, 5, 1. Evaluate u + v...Ch. 13.2 - What is the magnitude of a vector joining two...Ch. 13.2 - Which point is farther from the origin, (3, 1, 2)...Ch. 13.2 - Express the vector from P(1, 4, 6) to Q(1, 3, 6)...Ch. 13.2 - Points in 3 Find the coordinates of the vertices...Ch. 13.2 - Points in 3 Find the coordinates of the vertices...Ch. 13.2 - Points in 3 Find the coordinates of the vertices...Ch. 13.2 - Points in 3 Find the coordinates of the vertices...Ch. 13.2 - Plotting points in 3 For each point P(x, y, z)...Ch. 13.2 - Plotting points in 3 For each point P(x, y, z)...Ch. 13.2 - Sketching planes Sketch the following planes in...Ch. 13.2 - Sketching planes Sketch the following planes in...Ch. 13.2 - Sketching planes Sketch the following planes in...Ch. 13.2 - Sketching planes Sketch the following planes in...Ch. 13.2 - Sketching planes Sketch the following planes in...Ch. 13.2 - Sketching planes Sketch the following planes in...Ch. 13.2 - Planes Sketch the plane parallel to the xy-plane...Ch. 13.2 - Prob. 22ECh. 13.2 - Spheres and balls Find an equation or inequality...Ch. 13.2 - Spheres and balls Find an equation or inequality...Ch. 13.2 - Spheres and balls Find an equation or inequality...Ch. 13.2 - Spheres and balls Find an equation or inequality...Ch. 13.2 - Midpoints and spheres Find an equation of the...Ch. 13.2 - Midpoints and spheres Find an equation of the...Ch. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Prob. 34ECh. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Identifying sets Give a geometric description of...Ch. 13.2 - Prob. 39ECh. 13.2 - Prob. 40ECh. 13.2 - Prob. 41ECh. 13.2 - Prob. 42ECh. 13.2 - Prob. 43ECh. 13.2 - Prob. 44ECh. 13.2 - Unit vectors and magnitude Consider the following...Ch. 13.2 - Unit vectors and magnitude Consider the following...Ch. 13.2 - Unit vectors and magnitude Consider the following...Ch. 13.2 - Unit vectors and magnitude Consider the following...Ch. 13.2 - Prob. 49ECh. 13.2 - Unit vectors and magnitude Consider the following...Ch. 13.2 - Flight in crosswinds A model airplane is flying...Ch. 13.2 - Another crosswind flight A model airplane is...Ch. 13.2 - Crosswinds A small plane is flying horizontally...Ch. 13.2 - Prob. 54ECh. 13.2 - Prob. 55ECh. 13.2 - Maintaining equilibrium An object is acted upon by...Ch. 13.2 - Explain why or why not Determine whether the...Ch. 13.2 - Sets of points Describe with a sketch the sets of...Ch. 13.2 - Sets of points Describe with a sketch the sets of...Ch. 13.2 - Sets of points Describe with a sketch the sets of...Ch. 13.2 - Sets of points 61. Give a geometric description of...Ch. 13.2 - Sets of points 62. Give a geometric description of...Ch. 13.2 - Sets of points 63. Give a geometric description of...Ch. 13.2 - Sets of points 64. Give a geometric description of...Ch. 13.2 - Prob. 65ECh. 13.2 - Prob. 66ECh. 13.2 - Write the vector v = 2, 4, 4 as a product of its...Ch. 13.2 - Find the vector of length 10 with the same...Ch. 13.2 - Find a vector of length 5 in the direction...Ch. 13.2 - Prob. 70ECh. 13.2 - Prob. 71ECh. 13.2 - Parallel vectors of varying lengths Find vectors...Ch. 13.2 - Parallel vectors of varying lengths Find vectors...Ch. 13.2 - Collinear points Determine the values of x and y...Ch. 13.2 - Collinear points Determine whether the points P,...Ch. 13.2 - Lengths of the diagonals of a box What is the...Ch. 13.2 - Three-cable load A 500-kg load hangs from three...Ch. 13.2 - Four-cable load A 500-lb load hangs from four...Ch. 13.2 - Possible parallelograms The points O(0, 0, 0),...Ch. 13.2 - Prob. 80ECh. 13.2 - Midpoint formula Prove that the midpoint of the...Ch. 13.2 - Equation of a sphere For constants a, b, c, and d,...Ch. 13.2 - Prob. 83ECh. 13.2 - Medians of a trianglewith coordinates In contrast...Ch. 13.2 - The amazing quadrilateral propertycoordinate free...Ch. 13.2 - The amazing quadrilateral property-with...Ch. 13.3 - Sketch two nonzero vectors u and v with = 0....Ch. 13.3 - Use Theorem 13.1 to computr the dot products i j,...Ch. 13.3 - Let u = 4i 3j. By inspection (not calculations),...Ch. 13.3 - Express the dot product of u and v in terms of...Ch. 13.3 - Express the dot product of u and v in terms of the...Ch. 13.3 - Compute 2, 3, 6 1, 8, 3.Ch. 13.3 - Prob. 4ECh. 13.3 - Prob. 5ECh. 13.3 - Find the angle between u and v if scalvu = 2 and...Ch. 13.3 - Find projvu if scalvu 2 and v 2,1,2.Ch. 13.3 - Use a dot product to determine whether the vectors...Ch. 13.3 - Prob. 9ECh. 13.3 - Prob. 10ECh. 13.3 - Suppose v is a nonzero position vector in the...Ch. 13.3 - Suppose v is a nonzero position vector in...Ch. 13.3 - Prob. 13ECh. 13.3 - Prob. 14ECh. 13.3 - Prob. 15ECh. 13.3 - Prob. 16ECh. 13.3 - Prob. 17ECh. 13.3 - Prob. 18ECh. 13.3 - Prob. 19ECh. 13.3 - Prob. 20ECh. 13.3 - Prob. 21ECh. 13.3 - Prob. 22ECh. 13.3 - Prob. 23ECh. 13.3 - Prob. 24ECh. 13.3 - Prob. 25ECh. 13.3 - Prob. 26ECh. 13.3 - Prob. 27ECh. 13.3 - Prob. 28ECh. 13.3 - Angles of a triangle For the given points P, Q,...Ch. 13.3 - Angles of a triangle For the given points P, Q,...Ch. 13.3 - Sketching orthogonal projections Find projvu and...Ch. 13.3 - Sketching orthogonal projections Find projvu and...Ch. 13.3 - Sketching orthogonal projections Find projvu and...Ch. 13.3 - Sketching orthogonal projections Find projvu and...Ch. 13.3 - Calculating orthogonal projections For the given...Ch. 13.3 - Calculating orthogonal projections For the given...Ch. 13.3 - Calculating orthogonal projections For the given...Ch. 13.3 - Calculating orthogonal projections For the given...Ch. 13.3 - Prob. 39ECh. 13.3 - Calculating orthogonal projections For the given...Ch. 13.3 - Prob. 41ECh. 13.3 - Computing work Calculate the work done in the...Ch. 13.3 - Prob. 43ECh. 13.3 - Computing work Calculate the work done in the...Ch. 13.3 - Computing work Calculate the work done in the...Ch. 13.3 - Prob. 46ECh. 13.3 - Parallel and normal forces Find the components of...Ch. 13.3 - Parallel and normal forces Find the components of...Ch. 13.3 - Prob. 49ECh. 13.3 - Forces on an inclined plane An object on an...Ch. 13.3 - Prob. 51ECh. 13.3 - For what value of a is the vector v = 4,3,7...Ch. 13.3 - For what value of c is the vector v = 2,5,c...Ch. 13.3 - Orthogonal vectors Let a and b be real numbers....Ch. 13.3 - Orthogonal vectors Let a and b be real numbers....Ch. 13.3 - Prob. 56ECh. 13.3 - Prob. 57ECh. 13.3 - Vectors with equal projections Given a fixed...Ch. 13.3 - Vectors with equal projections Given a fixed...Ch. 13.3 - Vectors with equal projections Given a fixed...Ch. 13.3 - Vectors with equal projections Given a fixed...Ch. 13.3 - Decomposing vectors For the following vectors u...Ch. 13.3 - Decomposing vectors For the following vectors u...Ch. 13.3 - Decomposing vectors For the following vectors u...Ch. 13.3 - Decomposing vectors For the following vectors u...Ch. 13.3 - An alternative line definition Given a fixed point...Ch. 13.3 - An alternative line definition Given a fixed point...Ch. 13.3 - Prob. 68ECh. 13.3 - An alternative line definition Given a fixed point...Ch. 13.3 - Orthogonal unit vectors in 3 Consider the vectors...Ch. 13.3 - Orthogonal unit vectors in 3 Consider the vectors...Ch. 13.3 - Orthogonal unit vectors in 3 Consider the vectors...Ch. 13.3 - Orthogonal unit vectors in 3 Consider the vectors...Ch. 13.3 - Flow through a circle Suppose water flows in a...Ch. 13.3 - Heat flux Let D be a solid heat-conducting cube...Ch. 13.3 - Hexagonal circle packing The German mathematician...Ch. 13.3 - Hexagonal sphere packing Imagine three unit...Ch. 13.3 - Properties of dot products Let u = u1, u2, u3, v =...Ch. 13.3 - Prob. 79ECh. 13.3 - Prob. 80ECh. 13.3 - Prob. 81ECh. 13.3 - Properties of dot products Let u = u1, u2, u3, v =...Ch. 13.3 - Direction angles and cosines Let v = a, b, c and...Ch. 13.3 - Prob. 84ECh. 13.3 - Prob. 85ECh. 13.3 - CauchySchwarz Inequality The definition u v = |u|...Ch. 13.3 - CauchySchwarz Inequality The definition u v = |u|...Ch. 13.3 - CauchySchwarz Inequality The definition u v = |u|...Ch. 13.3 - Diagonals of a parallelogram Consider the...Ch. 13.4 - Prob. 1QCCh. 13.4 - Explain why the vector 2u 3v points in the same...Ch. 13.4 - A good check on a product calculation is to verify...Ch. 13.4 - What is the magnitude of the cross product of two...Ch. 13.4 - Prob. 2ECh. 13.4 - Suppose u and v are nonzero vectors. What is the...Ch. 13.4 - Use a geometric argument to explain why u (u v) =...Ch. 13.4 - Compute |u v| if u and v are unit vectors and the...Ch. 13.4 - Compute |u v| if |u| = 3 and |v| = 4 and the...Ch. 13.4 - Prob. 7ECh. 13.4 - For any vector v in 3, explain why v v = 0.Ch. 13.4 - Explain how to use a determinant to compute u v.Ch. 13.4 - Explain how to find the torque produced by a force...Ch. 13.4 - Cross products from the definition Find the cross...Ch. 13.4 - Cross products from the definition Find the cross...Ch. 13.4 - Cross products from the definition Sketch the...Ch. 13.4 - Prob. 14ECh. 13.4 - Prob. 15ECh. 13.4 - Prob. 16ECh. 13.4 - Coordinate unit vectors Compute the following...Ch. 13.4 - Prob. 18ECh. 13.4 - Prob. 19ECh. 13.4 - Coordinate unit vectors Compute the following...Ch. 13.4 - Prob. 21ECh. 13.4 - Prob. 22ECh. 13.4 - Prob. 23ECh. 13.4 - Prob. 24ECh. 13.4 - Prob. 25ECh. 13.4 - Prob. 26ECh. 13.4 - Prob. 27ECh. 13.4 - Prob. 28ECh. 13.4 - Area of a parallelogram Find the area of the...Ch. 13.4 - Area of a parallelogram Find the area of the...Ch. 13.4 - Area of a parallelogram Find the area of the...Ch. 13.4 - Area of a parallelogram Find the area of the...Ch. 13.4 - Area of a triangle For the given points A, B, and...Ch. 13.4 - Areas of triangles Find the area of the following...Ch. 13.4 - Area of a triangle For the given points A, B, and...Ch. 13.4 - Area of a triangle For the given points A, B, and...Ch. 13.4 - Areas of triangles Find the area of the following...Ch. 13.4 - Areas of triangles Find the area of the following...Ch. 13.4 - Collinear points and cross products Explain why...Ch. 13.4 - Collinear points Use cross products to determine...Ch. 13.4 - Collinear points Use cross products to determine...Ch. 13.4 - Orthogonal vectors Find a vector orthogonal to the...Ch. 13.4 - Orthogonal vectors Find a vector orthogonal to the...Ch. 13.4 - Orthogonal vectors Find a vector orthogonal to the...Ch. 13.4 - Computing torque Answer the following questions...Ch. 13.4 - Computing torque Answer the following questions...Ch. 13.4 - Computing torque Answer the following questions...Ch. 13.4 - Computing torque Answer the following questions...Ch. 13.4 - Prob. 49ECh. 13.4 - Prob. 50ECh. 13.4 - Prob. 51ECh. 13.4 - Arm torque A horizontally outstretched arm...Ch. 13.4 - Force on a moving charge Answer the following...Ch. 13.4 - Prob. 54ECh. 13.4 - Prob. 55ECh. 13.4 - Force on a moving charge Answer the following...Ch. 13.4 - Prob. 57ECh. 13.4 - Finding an unknown Find the value of a such that...Ch. 13.4 - Prob. 59ECh. 13.4 - Prob. 60ECh. 13.4 - Prob. 61ECh. 13.4 - Express u, v, and w in terms of their components...Ch. 13.4 - Prob. 63ECh. 13.4 - Prob. 64ECh. 13.4 - Scalar triple product Another operation with...Ch. 13.4 - Prob. 66ECh. 13.4 - Prob. 67ECh. 13.4 - Three proofs Prove that u u = 0 in three ways. a....Ch. 13.4 - Associative property Prove in two ways that for...Ch. 13.4 - Prob. 70ECh. 13.4 - Prob. 71ECh. 13.4 - Prob. 72ECh. 13.4 - Identities Prove the following identities. Assume...Ch. 13.4 - Prob. 74ECh. 13.4 - Cross product equations Suppose u and v are known...Ch. 13.5 - Describe the line r = t k. for t . Describe the...Ch. 13.5 - In the equation of the line x, y, zx0, y0, z0x1 ...Ch. 13.5 - Find the distance between the point Q(1, 0, 3) and...Ch. 13.5 - Consider the equation of a plare in the form n P0P...Ch. 13.5 - Verify that in Example 6, the same equation for...Ch. 13.5 - Determine whether the planes 2x 3y + 6z = 12 and...Ch. 13.5 - Find a position vector that is parallel to the...Ch. 13.5 - Find the parametric equations of the line r =...Ch. 13.5 - Explain how to find a vector in the direction of...Ch. 13.5 - What is an equation of the line through the points...Ch. 13.5 - Determine whether the plane x + y + z = 9 and the...Ch. 13.5 - Determine whether the plane x + y + z = 9 and the...Ch. 13.5 - Give two pieces of information which, taken...Ch. 13.5 - Find a vector normal to the plane 2x 3y + 4z =...Ch. 13.5 - Where does the plane 2x 3y + 4z = 12 intersect...Ch. 13.5 - Give an equation of the plane with a normal vector...Ch. 13.5 - Equations of lines Find equations of the following...Ch. 13.5 - Equations of lines Find equations of the following...Ch. 13.5 - Equations of lines Find equations of the following...Ch. 13.5 - Equations of lines Find both the parametric and...Ch. 13.5 - Equations of lines Find equations of the following...Ch. 13.5 - Equations of lines Find both the parametric and...Ch. 13.5 - Equations of lines Find both the parametric and...Ch. 13.5 - Equations of lines Find equations of the following...Ch. 13.5 - Equations of lines Find equations of the following...Ch. 13.5 - Equations of lines Find equations of the following...Ch. 13.5 - Prob. 21ECh. 13.5 - Equations of lines Find equations of the following...Ch. 13.5 - Prob. 23ECh. 13.5 - Prob. 24ECh. 13.5 - Equations of lines Find both the parametric and...Ch. 13.5 - Equations of lines Find both the parametric and...Ch. 13.5 - Line segments Find an equation of the line segment...Ch. 13.5 - Line segments Find an equation of the line segment...Ch. 13.5 - Line segments Find an equation of the line segment...Ch. 13.5 - Line segments Find an equation of the line segment...Ch. 13.5 - Parallel, Intersecting, or skew lines Determine...Ch. 13.5 - Parallel, Intersecting, or skew lines Determine...Ch. 13.5 - Parallel, Intersecting, or skew lines Determine...Ch. 13.5 - Parallel, Intersecting, or skew lines Determine...Ch. 13.5 - Parallel, Intersecting, or skew lines Determine...Ch. 13.5 - Parallel, Intersecting, or skew lines Determine...Ch. 13.5 - Parallel, Intersecting, or skew lines Determine...Ch. 13.5 - Intersecting lines and colliding particles...Ch. 13.5 - Distance from a point to a line Find the distance...Ch. 13.5 - Distance from a point to a line Find the distance...Ch. 13.5 - Billiards shot A cue ball in a billiards video...Ch. 13.5 - Prob. 42ECh. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equation of a plane Find an equation of the plane...Ch. 13.5 - Equation of a plane Find an equation of the plane...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Prob. 55ECh. 13.5 - Prob. 56ECh. 13.5 - Equations of planes Find an equation of the...Ch. 13.5 - Prob. 58ECh. 13.5 - Parallel planes is the line x = t + 1, y = 2t + 3,...Ch. 13.5 - Do the lines x = t, y = 2t + 1, z = 3t + 4 and x =...Ch. 13.5 - Properties of planes Find the points at which the...Ch. 13.5 - Prob. 62ECh. 13.5 - Properties of planes Find the points at which the...Ch. 13.5 - Prob. 64ECh. 13.5 - Pairs of planes Determine whether the following...Ch. 13.5 - Pairs of planes Determine whether the following...Ch. 13.5 - Pairs of planes Determine whether the following...Ch. 13.5 - Pairs of planes Determine whether the following...Ch. 13.5 - Equations of planes For the following sets of...Ch. 13.5 - Equations of planes For the following sets of...Ch. 13.5 - Lines normal to planes Find an equation of the...Ch. 13.5 - Lines normal to planes Find an equation of the...Ch. 13.5 - Intersecting planes Find an equation of the line...Ch. 13.5 - Intersecting planes Find an equation of the line...Ch. 13.5 - Intersecting planes Find an equation of the line...Ch. 13.5 - Intersecting planes Find an equation of the line...Ch. 13.5 - Line-plane intersections Find the point (if it...Ch. 13.5 - Line-plane intersections Find the point (if it...Ch. 13.5 - Line-plane intersections Find the point (if it...Ch. 13.5 - Line-plane intersections Find the point (if it...Ch. 13.5 - Explain why or why not Determine whether the...Ch. 13.5 - Distance from a point to a plane Suppose P is a...Ch. 13.5 - Find the distance from the point Q (6, 2, 4) to...Ch. 13.5 - Find the distance from the point Q (1, 2, 4) to...Ch. 13.5 - Symmetric equations for a line If we solve fort in...Ch. 13.5 - Symmetric equations for a line If we solve fort in...Ch. 13.5 - Angle between planes The angle between two planes...Ch. 13.5 - Prob. 88ECh. 13.5 - Prob. 89ECh. 13.5 - Orthogonal plane Find an equation of the plane...Ch. 13.5 - Three intersecting planes Describe the set of all...Ch. 13.5 - Three intersecting planes Describe the set of all...Ch. 13.6 - To which coordinate axis in 3 is the cylinder z 2...Ch. 13.6 - Explain why the elliptic cylinder discussed in...Ch. 13.6 - Assume 0 c b a in the general equation of an...Ch. 13.6 - The elliptic paraboloid x=y23+z27 is a bowl-shaped...Ch. 13.6 - Which coordinate axis is the axis of the...Ch. 13.6 - Prob. 6QCCh. 13.6 - To which coordinate axes are the following...Ch. 13.6 - Describe the graph of x = z2 in 3.Ch. 13.6 - What is a trace of a surface?Ch. 13.6 - What is the name of the surface defined by the...Ch. 13.6 - What is the name of the surface defined by the...Ch. 13.6 - What is the name of the surface defined by the...Ch. 13.6 - Cylinders in 3 Consider the following cylinders in...Ch. 13.6 - Cylinders in 3 Consider the following cylinders in...Ch. 13.6 - Cylinders in 3 Consider the following cylinders in...Ch. 13.6 - Cylinders in 3 Consider the following cylinders in...Ch. 13.6 - Cylinders in 3 Consider the following cylinders in...Ch. 13.6 - Cylinders in 3 Consider the following cylinders in...Ch. 13.6 - Cylinders in 3 Consider the following cylinders in...Ch. 13.6 - Cylinders in 3 Consider the following cylinders in...Ch. 13.6 - Identifying quadric surfaces Identify the...Ch. 13.6 - Identifying quadric surfaces Identify the...Ch. 13.6 - Identifying quadric surfaces Identify the...Ch. 13.6 - Identifying quadric surfaces Identify the...Ch. 13.6 - Identifying quadric surfaces Identify the...Ch. 13.6 - Identifying quadric surfaces Identify the...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify the following...Ch. 13.6 - Identifying surfaces Identify the following...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Prob. 38ECh. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Prob. 42ECh. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Prob. 44ECh. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Prob. 47ECh. 13.6 - Prob. 48ECh. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Quadric surfaces Consider the following equations...Ch. 13.6 - Prob. 52ECh. 13.6 - Prob. 53ECh. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Identifying surfaces Identify and briefly describe...Ch. 13.6 - Prob. 59ECh. 13.6 - Matching graphs with equations Match equations af...Ch. 13.6 - Explorations and Challenges 61. Solids of...Ch. 13.6 - Prob. 62ECh. 13.6 - Prob. 63ECh. 13.6 - Light cones The idea of a light cone appears in...Ch. 13.6 - Prob. 65ECh. 13.6 - Hand tracking Researchers are developing hand...Ch. 13.6 - Designing a snow cone A surface, having the shape...Ch. 13.6 - Designing a glass The outer, lateral side of a...Ch. 13 - Explain why or why not Determine whether the...Ch. 13 - Prob. 2RECh. 13 - Prob. 3RECh. 13 - Prob. 4RECh. 13 - Prob. 5RECh. 13 - Working with vectors Let u = 2, 4, 5 and v = 6,...Ch. 13 - Working with vectors Let u = 2, 4, 5 and v = 6,...Ch. 13 - Prob. 8RECh. 13 - working with vectors Let u = 2,4,5 , v = 6,10,2...Ch. 13 - working with vectors Let u = 2,4,5 , v = 6,10,2...Ch. 13 - working with vectors Let u = 2,4,5 , v = 6,10,2...Ch. 13 - working with vectors Let u = 2,4,5 , v = 6,10,2...Ch. 13 - working with vectors Let u = 2,4,5 , v = 6,10,2...Ch. 13 - working with vectors Let u = 2,4,5 , v = 6,10,2...Ch. 13 - working with vectors Let u = 2,4,5 , v = 6,10,2...Ch. 13 - Scalar multiples Find scalars a, b, and c such...Ch. 13 - Velocity vectors Assume the positive x-axis points...Ch. 13 - Prob. 18RECh. 13 - Spheres and balls Use set notation to describe the...Ch. 13 - Spheres and balls Use set notation to describe the...Ch. 13 - Spheres and balls Use set notation to describe the...Ch. 13 - Identifying sets. Give a geometric description of...Ch. 13 - Identifying sets. Give a geometric description of...Ch. 13 - Identifying sets. Give a geometric description of...Ch. 13 - Identifying sets. Give a geometric description of...Ch. 13 - Prob. 26RECh. 13 - Prob. 27RECh. 13 - Cross winds A small plane is flying north in calm...Ch. 13 - Prob. 29RECh. 13 - Canoe in a current A woman in a canoe paddles cue...Ch. 13 - Sets of points Describe the set of points...Ch. 13 - Angles and projections a. Find the angle between u...Ch. 13 - Prob. 33RECh. 13 - Prob. 34RECh. 13 - Computing work Calculate the work done in the...Ch. 13 - Computing work Calculate the work done in the...Ch. 13 - Prob. 37RECh. 13 - Inclined plane A 1804b map stands on a hillside...Ch. 13 - Area of a parallelogram Find the area of the...Ch. 13 - Area of a triangle Find the area of the triangle...Ch. 13 - Vectors normal to a plane Find a unit vector...Ch. 13 - Angle in two ways Find the angle between 2, 0, 2...Ch. 13 - Prob. 43RECh. 13 - Suppose you apply a force of |F| = 50 N near the...Ch. 13 - Prob. 45RECh. 13 - Lines in space Find an equation of the following...Ch. 13 - Lines in space Find an equation of the following...Ch. 13 - Lines in space Find an equation of the following...Ch. 13 - Lines in space Find an equation of the following...Ch. 13 - Lines in space Find an equation of the following...Ch. 13 - Equations of planes Consider the plane passing...Ch. 13 - Intersecting planes Find an equation of the line...Ch. 13 - Intersecting planes Find an equation of the line...Ch. 13 - Equations of planes Find an equation of the...Ch. 13 - Prob. 55RECh. 13 - Prob. 56RECh. 13 - Equations of planes Find an equation of the...Ch. 13 - Distance from a point to a line Find the distance...Ch. 13 - Distance from a point to a plane Find the distance...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Prob. 73RECh. 13 - Identifying surfaces Consider the surfaces defined...Ch. 13 - Prob. 75RECh. 13 - Designing a water bottle The lateral surface of a...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Women’s Heights Assume that college women’s heights are approximately Normally distributed with a mean of 65 in...

Introductory Statistics

Fill in each blank so that the resulting statement is true. An equation that expresses a relationship between t...

Algebra and Trigonometry (6th Edition)

The null hypothesis, alternative hypothesis, test statistic, P-value and state the conclusion. To test: Whether...

Elementary Statistics

Derivatives of inverse sine Evaluate the derivatives of the following functions. 10. f(x) = sin1 (ln x)

Calculus: Early Transcendentals (2nd Edition)

In Exercises 1-8, describe the given region in polar coordinates. 2.

University Calculus: Early Transcendentals (4th Edition)

For a population containing N=902 individual, what code number would you assign for a. the first person on the ...

Basic Business Statistics, Student Value Edition

Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Text book image
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
How to find the magnitude and direction of a given vector; Author: Brian McLogan;https://www.youtube.com/watch?v=4qE-ZrR_NxI;License: Standard YouTube License, CC-BY
Linear Algebra for Computer Scientists. 2. Magnitude of a Vector; Author: Computer Science;https://www.youtube.com/watch?v=ElnuSJyUdR4;License: Standard YouTube License, CC-BY