
To find: Instantaneous Velocity on the Moon Neil Armstrong throws a ball down into a crater on the moon. The height (in feet) of the ball from the bottom of the crater after seconds is given in the following table:
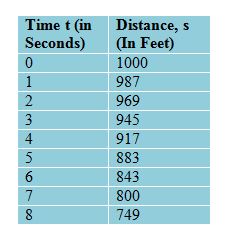
a. Find the average velocity from to seconds.
To find: Instantaneous Velocity on the Moon Neil Armstrong throws a ball down into a crater on the moon. The height (in feet) of the ball from the bottom of the crater after seconds is given in the following table:

b. Find the average velocity from to seconds.
To find: Instantaneous Velocity on the Moon Neil Armstrong throws a ball down into a crater on the moon. The height (in feet) of the ball from the bottom of the crater after seconds is given in the following table:

c. Find the average velocity from to seconds.
To find: Instantaneous Velocity on the Moon Neil Armstrong throws a ball down into a crater on the moon. The height (in feet) of the ball from the bottom of the crater after seconds is given in the following table:

d. Using a graphing utility, find the quadratic function of best fit.
To find: Instantaneous Velocity on the Moon Neil Armstrong throws a ball down into a crater on the moon. The height (in feet) of the ball from the bottom of the crater after seconds is given in the following table:

e. Using the function found in part , determine the instantaneous velocity at second.
Want to see the full answer?
Check out a sample textbook solution
Chapter 13 Solutions
Precalculus: Concepts Through Functions, A Unit Circle Approach to Trigonometry (4th Edition)
- i need help pleasearrow_forwardQuestion 4 Find an equation of (a) The plane through the point (2, 0, 1) and perpendicular to the line x = y=2t, z=3+4t. 3t, (b) The plane through the point (3, −2, 8) and parallel to the plane z = x+y. (c) The plane that contains the line x = parallel to the plane 5x + 2y + z = 1. 1+t, y2t, z = 43t and is (d) The plane that passes through the point (1,2,3) and contains the line x = 3t, y=1+t, and z = 2 – t. (e) The plane that contains the lines L₁ : x = 1 + t, y = 1 − t, z = = L2 x 2s, y = s, z = 2. 2t andarrow_forwardcan you explain why the correct answer is Aarrow_forward
 Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning





