Chapter 13.3, Problem 67E

An alternative line definition Given a fixed point P₀ (x₀, y₀) and a nonzero vector n = $\langle a,b\rangle$ the set of points $P\langle x,y\rangle$ for which $\stackrel{\rightharpoonup }{P_{0}P}$ is orthogonal to n is a line ℓ (see figure). The vector n is called a normal vector or a vector normal to ℓ.

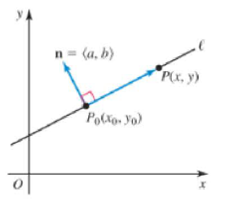
67. Use the result of Exercise 66 to find an equation of the line passing through the point P₀ (2, 6) with a normal vector n = (3, ‒7). Write the final answer in the form ax + by = c.

66. Show that the equation of the line passing through P₀ (x₀, y₀) with a normal vector n = $\langle a,b\rangle$ is a(x ‒ x₀) + b(y ‒ y₀) = 0. (Hint: For a point P(x, y) on ℓ, examine n · $\stackrel{\rightharpoonup }{P_{0}P}$.)