EBK MATHEMATICS FOR ELEMENTARY TEACHERS
5th Edition
ISBN: 9780134506609
Author: Beckmann
Publisher: PEARSON CUSTOM PUB.(CONSIGNMENT)
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 13.1, Problem 9P
Two gorgeous polyhedra can be created by stellating an icosahedron and a dodecahedron. SteI/ating means making starlike. Imagine turning each face of an icosahedron into a “star point"-namely, a pyramid whose base is a triangular face of th icosahedron. Likewise, imagine turning each face of a dodecahedron into a star point-namely, a pyramid whose base is a pentagonal face of the dodecahedron. A stellated icosahedron will then have 20 star points, whereas a stellated dodecahedron will have 12 star points.
a. Make 20 copies of Figure 13.15 on card stock. Cut, fold, and tape them to make 20 triangle-based pyramid star points. (The pattern makes star-point pyramids that don’t have bases.) Tape the star points together as though you were making an icosahedron out of their (open) bases.
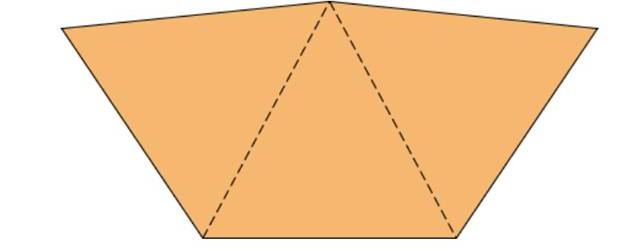
Figure 13.15 Pattern for a star point of an icosahedron.
b. Make 12 copies of Figure 13.16 on card stock. Cut, fold, and tape them to make 12 pentagon-based pyramid star points. (The pattern makes star point pyramids that don’t have bases.) Tape the star points together as though you were making a dodecahedron out of their (open) bases.
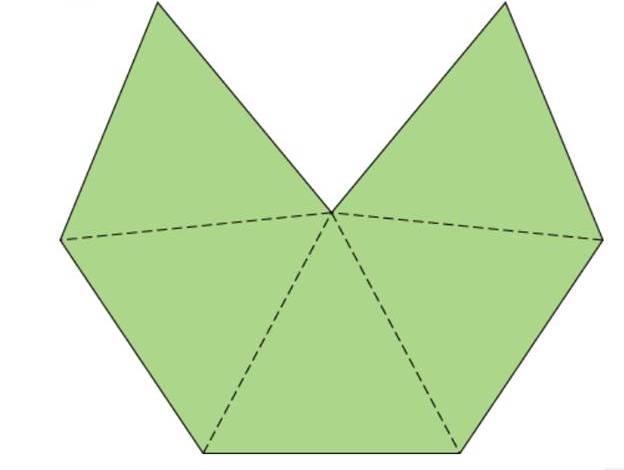
Figure 13.16 pattern for a star point of a dodecahedron
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Task Description:
Read the following case study and answer the questions that follow.
Ella is a 9-year-old third-grade student in an inclusive classroom. She has been diagnosed with Emotional and Behavioural Disorder (EBD). She has been struggling academically and socially due to
challenges related to self-regulation, impulsivity, and emotional outbursts. Ella's behaviour includes frequent tantrums, defiance toward authority figures, and difficulty forming positive relationships with peers. Despite her challenges, Ella shows an interest in art and creative activities and demonstrates strong verbal skills when calm.
Describe 2 strategies that could be implemented that could help Ella regulate her emotions in class (4 marks)
Explain 2 strategies that could improve Ella’s social skills (4 marks)
Identify 2 accommodations that could be implemented to support Ella academic progress and provide a rationale for your recommendation.(6 marks)
Provide a detailed explanation of 2 ways…
1. Iodine-131 is tone of the most commonly used radioactive isotopes of iodine. It is used to treat hyper-
thyroidism and some kinds of thyroid cancer.
(a) Iodine-131 has a half-life of about 8 days. Find an expression for I(t), the mass of Iodine-131
remaining after t days, in terms of t and Io, the initial mass of Iodine-131 present at time t = 0.
(b) If a dose of 0.9 mg of Iodine-131 is administered, how much is still present after 24 hours?
(c) How much Iodine-131 is present after one week? Does your answer make sense?
Question 2: When John started his first job, his first end-of-year salary was $82,500. In the following years, he received salary raises as shown in the following table.
Fill the Table: Fill the following table showing his end-of-year salary for each year. I have already provided the end-of-year salaries for the first three years. Calculate the end-of-year salaries for the remaining years using Excel. (If you Excel answer for the top 3 cells is not the same as the one in the following table, your formula / approach is incorrect) (2 points)
Geometric Mean of Salary Raises: Calculate the geometric mean of the salary raises using the percentage figures provided in the second column named “% Raise”. (The geometric mean for this calculation should be nearly identical to the arithmetic mean. If your answer deviates significantly from the mean, it's likely incorrect. 2 points)
Starting salary
% Raise
Raise
Salary after raise
75000
10%
7500
82500
82500
4%
3300…
Chapter 13 Solutions
EBK MATHEMATICS FOR ELEMENTARY TEACHERS
Ch. 13.1 - For each of the following solid shapes, find at...Ch. 13.1 - Answer the following questions without using a...Ch. 13.1 - Answer the following questions without using a...Ch. 13.1 - Recall that an n-gon is a polygon with n side For...Ch. 13.1 - This problem goes with Class Activity 13C on the...Ch. 13.1 - Referring to the descriptions of the Platonic...Ch. 13.1 - A cube is a polyhedron that has 3 square faces...Ch. 13.1 - The Platonic solids are convex polyhedra with...Ch. 13.1 - Two gorgeous polyhedra can be created by...Ch. 13.2 - Find all the different nets for a tetrahedron made...
Ch. 13.2 - Make three different nets that could be cut out,...Ch. 13.2 - Describe or show how to make a cylinder without...Ch. 13.2 - If a cardboard box (rectangular prism) with a top,...Ch. 13.2 - Use a ruler and compass to help you make a pattern...Ch. 13.2 - Use a ruler and compass to help you make a pattern...Ch. 13.2 - Use a ruler and compass to help you make a pattern...Ch. 13.2 - Prob. 8PCh. 13.2 - Make a pattern for the “bottom portion” (frustum)...Ch. 13.2 - A company will manufacture a tent that will have a...Ch. 13.2 - Prob. 11PCh. 13.2 - Prob. 12PCh. 13.2 - A popular brand of soup comes in cans that are 258...Ch. 13.2 - The lateral portion of a cone (the part other than...Ch. 13.2 - Make a pattern for a cone such that the lateral...Ch. 13.2 - Make a pattern for a cone such that the lateral...Ch. 13.2 - A cone with a circular base of radius 6 cm is to...Ch. 13.2 - Tim needs a sturdy cardboard box that is 3 ft tall...Ch. 13.2 - Prob. 19PCh. 13.2 - Prob. 20PCh. 13.2 - Prob. 21PCh. 13.2 - Prob. 22PCh. 13.2 - How many different nets an open top cubes an...Ch. 13.2 - Make three different nets that could be cut out,...Ch. 13.3 - Suppose that a student in your class wants to know...Ch. 13.3 - Students are sometimes confused about the...Ch. 13.3 - Young children sometimes think that tall...Ch. 13.3 - Students often confuse the surface area and the...Ch. 13.3 - In your own words, explain why the volume volume =...Ch. 13.3 - Discuss how to use blocks to explain why the...Ch. 13.3 - A cylindrical container has a base that is a...Ch. 13.3 - One liter of water is in a cylindrical container....Ch. 13.3 - Measure how fast water comes out of some faucet of...Ch. 13.3 - Find a gallon container, 3 half-gallon container,...Ch. 13.3 - One gallon is 3.79 L, and 1 cm3 holds 1 mL of...Ch. 13.3 - A cake recipe will make a round cake that is 6 in....Ch. 13.3 - A recipe for gingerbread makes a...Ch. 13.3 - The front (and back) of a greenhouse have the...Ch. 13.3 - Prob. 15PCh. 13.3 - Fifty pounds of wrapping paper are wound onto a...Ch. 13.3 - A conveyor belt dumps 2500 yd3 of gravel to form a...Ch. 13.3 - A construction company wants to know how much sand...Ch. 13.3 - One of the Hawaiian volcanoes is 30,000 ft high...Ch. 13.3 - Prob. 20PCh. 13.3 - Prob. 21PCh. 13.3 - A cone without a base is made from a...Ch. 13.3 - Prob. 23PCh. 13.3 - A cone without a base is made from 34 of a circle...Ch. 13.3 - A cone-shaped cup has a circular opening at the...Ch. 13.3 - Eight identical spherical raindrops join together...Ch. 13.4 - A tank in the shape of a rectangular prism has a...Ch. 13.4 - A container holds 5 liters. Initially, the...Ch. 13.4 - Aflsh tank in the shape of a rectangular prism is...Ch. 13.4 - Suppose that you have a recipe that calls for 200...Ch. 13.4 - Prob. 5P
Additional Math Textbook Solutions
Find more solutions based on key concepts
For Problems 23-28, write in simpler form, as in Example 4. logbFG
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Complete each statement with the correct term from the column on the right. Some of the choices may not be used...
Intermediate Algebra (13th Edition)
1. How much money is Joe earning when he’s 30?
Pathways To Math Literacy (looseleaf)
Let F be a continuous distribution function. If U is uniformly distributed on (0,1), find the distribution func...
A First Course in Probability (10th Edition)
23. A plant nursery sells two sizes of oak trees to landscapers. Large trees cost the nursery $120 from the gro...
College Algebra (Collegiate Math)
The largest polynomial that divides evenly into a list of polynomials is called the _______.
Elementary & Intermediate Algebra
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- d₁ ≥ ≥ dn ≥ 0 with di even. di≤k(k − 1) + + min{k, di} vi=k+1 T2.5: Let d1, d2,...,d be integers such that n - 1 Prove the equivalence of the Erdos-Gallai conditions: for each k = 1, 2, ………, n and the Edge-Count Criterion: Σier di + Σjeл(n − 1 − d;) ≥ |I||J| for all I, JC [n] with In J = 0.arrow_forwardT2.4: Let d₁arrow_forwardSolve the following boundary value problem using method of separation of variables: 1 ə ди r dr 70% (107) + 1 д²и = 0, 12802 -πarrow_forwardT2.3: Prove that there exists a connected graph with degrees d₁ ≥ d₂ >> dn if and only if d1, d2,..., dn is graphic, d ≥ 1 and di≥2n2. That is, some graph having degree sequence with these conditions is connected. Hint - Do not attempt to directly prove this using Erdos-Gallai conditions. Instead work with a realization and show that 2-switches can be used to make a connected graph with the same degree sequence. Facts that can be useful: a component (i.e., connected) with n₁ vertices and at least n₁ edges has a cycle. Note also that a 2-switch using edges from different components of a forest will not necessarily reduce the number of components. Make sure that you justify that your proof has a 2-switch that does decrease the number of components.arrow_forwardT2.2 Prove that a sequence s d₁, d₂,..., dn with n ≥ 3 of integers with 1≤d; ≤ n − 1 is the degree sequence of a connected unicyclic graph (i.e., with exactly one cycle) of order n if and only if at most n-3 terms of s are 1 and Σ di = 2n. (i) Prove it by induction along the lines of the inductive proof for trees. There will be a special case to handle when no d₂ = 1. (ii) Prove it by making use of the caterpillar construction. You may use the fact that adding an edge between 2 non-adjacent vertices of a tree creates a unicylic graph.arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forward= == T2.1: Prove that the necessary conditions for a degree sequence of a tree are sufficient by showing that if di 2n-2 there is a caterpillar with these degrees. Start the construction as follows: if d1, d2,...,d2 and d++1 = d = 1 construct a path v1, v2, ..., vt and add d; - 2 pendent edges to v, for j = 2,3,..., t₁, d₁ - 1 to v₁ and d₁ - 1 to v₁. Show that this construction results vj in a caterpillar with degrees d1, d2, ..., dnarrow_forwardDo the Laplace Transformation and give the answer in Partial Fractions. Also do the Inverted Laplace Transformation and explain step-by-step.arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forward12. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.508.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x + 16 dx X Need Help? Read It SUBMIT ANSWER 13. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.512.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) dx 8)(2x + 1) Need Help? Read It SUBMIT ANSWER 14. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.518.XP. Find the area of the region under the given curve from 1 to 5. y = x² +7 6x - x² Need Help? Read It ASK YOUR TEAarrow_forwardLakshmi planted 20 begonias, but her neighbor’s dog ate 7 of them. What percent of the begonias did the dog eat?arrow_forwardDETAILS MY NOTES SESSCALCET2 6.3.012. 6. [-/1 Points] Evaluate the integral. x-4 dx x² - 5x + 6 Need Help? Read It SUBMIT ANSWER 7. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.019. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x²+1 (x-6)(x-5)² dx Need Help? Read It SUBMIT ANSWER 8. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.021. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) ✓ x² 4 +4 dxarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGALElementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage LearningCollege Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Finite State Machine (Finite Automata); Author: Neso Academy;https://www.youtube.com/watch?v=Qa6csfkK7_I;License: Standard YouTube License, CC-BY
Finite State Machine (Prerequisites); Author: Neso Academy;https://www.youtube.com/watch?v=TpIBUeyOuv8;License: Standard YouTube License, CC-BY