Essential University Physics: Volume 1 (3rd Edition)
3rd Edition
ISBN: 9780321993724
Author: Richard Wolfson
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 13, Problem 89PP
Physicians and physiologists are interested in the long-term effects of apparent weightlessness on the human body. Among these effects are redistribution of body fluids to the upper body, loss of muscle tone, and overall mass loss. One method of measuring mass in the apparent weightlessness of an orbiting spacecraft is to strap the astronaut into a chairlike device mounted on springs (Fig. 13.39). This body mass measuring device (BMMD) is set oscillating in simple harmonic
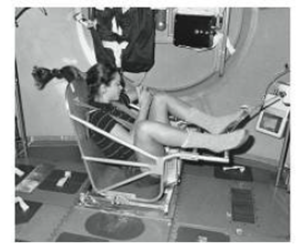
FIGURE 13.39 Astronaut Tamara Jernigan uses a body mass measuring device in the Spacelab Life Sciences Module (Passage Problems 87-90).
motion, and measurement of the oscillation period, along with the known spring constant and mass of the chair itself, then yields the astronaut’s mass. When a 60-kg astronaut is strapped into the 20-kg chair, the time for three oscillation periods is measured to be 6.0 s.
If an astronaut’s mass declines linearly with time while she’s in orbit, the oscillation period of the BMMD will
- a. decrease at an ever-decreasing rate.
- b. decrease linearly with time.
- c. decrease at an ever-increasing rate.
- d. increase linearly with time.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
An object oscillates horizontally on a frictionless surface. It’s position at any time t can be found using the function.
P(t) = 4 cos (t) + 2 sin (t) where t is measured in seconds and p(t) is measured in feet.
What is the object’s acceleration (in ft/s^2) at t = pi/3? Write the answer in exact terms.
As we’ve seen, astronauts measure their mass by measuring the period of oscillation when sitting in a chair connected to a spring. The Body Mass Measurement Device on Skylab, a 1970s space station, had a spring constant of 606 N/m. The empty chair oscillated with a period of 0.901 s. What is the mass of an astronaut who oscillates with a period of 2.09 s when sitting in the chair?
A mass hanging on a spring with spring constant 15 N/m has a period of 4 π s. (Note that π = 3.1415). What is the value of the mass (in kg)?
Chapter 13 Solutions
Essential University Physics: Volume 1 (3rd Edition)
Ch. 13.1 - A typical human heart rate is about 65 beats per...Ch. 13.2 - Two identical mass-spring systems are displaced...Ch. 13.3 - What happens to the period of a pendulum if (l)...Ch. 13.4 - Figure 13.18 shows the paths traced in the...Ch. 13.5 - Two different mass-spring systems are oscillating...Ch. 13.6 - The figure shows displacement-versus-time graphs...Ch. 13.7 - The photo shows a wineglass shattering in response...Ch. 13 - Is a vertically bouncing ball an example of...Ch. 13 - The vibration frequencies of molecules are much...Ch. 13 - What happens to the frequency of a simple harmonic...
Ch. 13 - If the spring of a simple harmonic oscillator is...Ch. 13 - How does the frequency of a simple harmonic...Ch. 13 - How would the frequency of a horizontal massspring...Ch. 13 - When in its cycle is the acceleration of an...Ch. 13 - Explain how simple harmonic motion might be used...Ch. 13 - One pendulum consists of a solid rod of mass m and...Ch. 13 - The x- and y-components of motion of a body are...Ch. 13 - Why is critical damping desirable in a cars...Ch. 13 - Explain why the frequency of a damped system is...Ch. 13 - Opera singers have been known to break glasses...Ch. 13 - What will happen to the period of a massspring...Ch. 13 - How can a system have more than one resonant...Ch. 13 - Prob. 16ECh. 13 - A violin string playing the note A oscillates at...Ch. 13 - The vibration frequency of a hydrogen chloride...Ch. 13 - Write expressions for the displacement x(t) in...Ch. 13 - The top of a skyscraper sways back and forth,...Ch. 13 - A hummingbirds wings vibrate at about 45 Hz. Whats...Ch. 13 - A 200-g mass is attached to a spring of constant k...Ch. 13 - An automobile suspension has an effective spring...Ch. 13 - The quartz crystal in a watch executes simple...Ch. 13 - A 342-g mass is attached to a spring and undergoes...Ch. 13 - A particle undergoes simple harmonic motion with...Ch. 13 - A particle undergoes simple harmonic motion with...Ch. 13 - How long should you make a simple pendulum so its...Ch. 13 - At the heart of a grandfather clock is a simple...Ch. 13 - A 622-g basketball with 24.0-cm diameter is...Ch. 13 - A meter stick is suspended from one end and set...Ch. 13 - A wheel rotates at 600 rpm. Viewed from the edge,...Ch. 13 - The x- and y-components of an objects motion are...Ch. 13 - A 450-g mass on a spring is oscillating at 1.2 Hz....Ch. 13 - A torsional oscillator of rotational inertia 1.6...Ch. 13 - Youre riding in a friends 1400-kg car with bad...Ch. 13 - The vibration of a piano string can be described...Ch. 13 - A massspring system has b/m = 0/5, where b is the...Ch. 13 - A cars front suspension has a natural frequency of...Ch. 13 - A simple model for carbon dioxide consists of...Ch. 13 - Two identical massspring systems consist of 430-g...Ch. 13 - The human eye and muscles that hold it can be...Ch. 13 - A mass m slides along a frictionless horizontal...Ch. 13 - Prob. 44PCh. 13 - A physics student, bored by a lecture on simple...Ch. 13 - A pendulum of length L is mounted in a rocket....Ch. 13 - The protein dynein powers the flagella that propel...Ch. 13 - A mass is attached to a vertical spring, which...Ch. 13 - Derive the period of a simple pendulum by...Ch. 13 - A solid disk of radius R is suspended from a...Ch. 13 - A thin steel beam is suspended from a crane and is...Ch. 13 - A cyclist turns her bicycle upside down to repair...Ch. 13 - An object undergoes simple harmonic motion in two...Ch. 13 - The muscles that drive insect wings minimize the...Ch. 13 - A pendulum consists of a 320-g solid ball 15.0 cm...Ch. 13 - If Jane and Tarzan are initially 8.0 m apart in...Ch. 13 - A small mass measuring device (SMMD) used for...Ch. 13 - A thin, uniform hoop of mass M and radius R is...Ch. 13 - A mass m is mounted between two springs with...Ch. 13 - The equation for an ellipse is (x2/a2) + (y2/b2) =...Ch. 13 - Show that the potential energy of a simple...Ch. 13 - The total energy of a massspring system is the sum...Ch. 13 - A solid cylinder of mass M and radius R is mounted...Ch. 13 - A mass m is free to slide on a frictionless track...Ch. 13 - A 250-g mass is mounted on a spring of constant k...Ch. 13 - A harmonic oscillator is underdamped if the...Ch. 13 - A massless spring with k = 74 N/m hangs from the...Ch. 13 - A meter stick is suspended from a frictionless rod...Ch. 13 - A particle of mass m has potential energy given by...Ch. 13 - Two balls with the same unknown mass m are mounted...Ch. 13 - Two mass-spring systems with the same mass are...Ch. 13 - Two mass-spring systems have the same mass and the...Ch. 13 - A 500-g mass is suspended from a thread 45 cm long...Ch. 13 - A 500-g block on a frictionless, horizontal...Ch. 13 - Repeat Problem 64 for a small solid ball of mass M...Ch. 13 - Youre working on the script of a movie whose plot...Ch. 13 - A 1.2-kg block rests on a frictionless surface and...Ch. 13 - A disk of radius R is suspended from a pivot...Ch. 13 - Prob. 79PCh. 13 - Youre a structural engineer working on a design...Ch. 13 - Show that x(t) = a cos t bsin t represents simple...Ch. 13 - Youre working for the summer with an ornithologist...Ch. 13 - While waiting for your plane to take off, you...Ch. 13 - Youre working for a playground equipment company,...Ch. 13 - Youve inherited your great-grandmothers mantle...Ch. 13 - This problem explores the nonlinear pendulum...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...Ch. 13 - Physicians and physiologists are interested in the...
Additional Science Textbook Solutions
Find more solutions based on key concepts
The Age of Earth. Some people still question whether we have a reasonable knowledge of the age of Earth or the ...
Life in the Universe (4th Edition)
What differences between gliders M and N could account for their differences in behavior during the collisions?
Tutorials in Introductory Physics
12. A 5.0 g coin is placed 15 cm from the center of a turntable. The coin has static and kinetic coefficients o...
Physics for Scientists and Engineers: A Strategic Approach, Vol. 1 (Chs 1-21) (4th Edition)
The rank for six points in an increasing order of speed.
Physics (5th Edition)
1. A 150-kg football player collides head-on with a 75-kg running back. During the collision, the heavier playe...
Physics: Principles with Applications
8. || A 68.5 kg skater Moving initially at 2.40 m/s on rough horizontal ice comes to rest uniformly in 3.52 s d...
College Physics (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- In an engine, a piston oscillates with simple harmonic motion so that its position varies according to the expression x=5.00cos(2t+6) where x is in centimeters and t is in seconds. At t = 0, find (a) the position of the piston, (b) its velocity, and (c) its acceleration. Find (d) the period and (e) the amplitude of the motion.arrow_forwardWe do not need the analogy in Equation 16.30 to write expressions for the translational displacement of a pendulum bob along the circular arc s(t), translational speed v(t), and translational acceleration a(t). Show that they are given by s(t) = smax cos (smpt + ) v(t) = vmax sin (smpt + ) a(t) = amax cos(smpt + ) respectively, where smax = max with being the length of the pendulum, vmax = smax smp, and amax = smax smp2.arrow_forwardFor each expression, identify the angular frequency , period T, initial phase and amplitude ymax of the oscillation. All values are in SI units. a. y(t) = 0.75 cos (14.5t) b. vy (t) = 0.75 sin (14.5t + /2) c. ay (t) = 14.5 cos (0.75t + /2) 16.3arrow_forward
- A mass hanging on a spring with spring constant 15 N/m has a period of 3 π s.(Note that π = 3.1415). What is the value of the mass (in kg)?arrow_forwardThe period of a simple pendulum (T) is measured as a function of length (L) on an unknown planet. The dependence of of L is linear (see the graph below). Use the slope of this graph to calculate the acceleration of gravity on this planet, in m/s2. 0.25 y = 0.0909x 0.2 0.15 0.1 0.05 Plot Area 0.5 1 1.5 2 2.5 L (m) T?/4 pi?(s')arrow_forwardA hole is drilled through the center of the earth. The gravitational force on a mass in that hole is mgr/R, where r is the distance of the mass from the earth’s center and R is the radius of the earth (6.4 x 10 6m).A mass dropped into the hole executes simple harmonic motion. Find the period of the motion. How does one-half this time compare with the time needed to fly in an air-’ plane halfway around the earth?arrow_forward
- A scientist wishes to determine the acceleration of gravity on the surface of the planet Nos'Kere by experimenting with a pendulum. The length of the pendulum is 3.2 m, and the period of the pendulum is 2.3 s. unitarrow_forwardIt is important to remember that, in a real pendulum, the value of L used in the period equation is the distance between the body's center of mass (CM) and the suspension point. To set up the simple pendulum experiment, a student used a string of length l=1,4644 m and a spherical body of uniform density and radius l0=3,45 cm as suspended mass. a) Calculate the value of L from the suspension point to the center of mass (CM) of the body in this setup and write your result in meters to 4 decimal places. b)If the oscillation is done in small amplitudes, in which the MHS approximation is valid, what is the period of the oscillation? Give your answer to 4 decimal places.arrow_forwardA 0.75 kg mass oscillates according to the equation x(t)=Acos(ωt). Here, A=0.67 m and ω=6.5 rad/s. What is the period, in seconds, of this mass?arrow_forward
- At an outdoor market, a bunch of bananasis set into oscillatory motion with an amplitude of 34.6313 cm on a spring with a springconstant of 14.7634 N/m. The mass of thebananas is 43.2987 kg.What is the maximum speed of the bananas?Answer in units of m/s.arrow_forwardThe motion of a body is described by the equation y = 2.70 sin(0.160πt), where t is in seconds and y is in meters. (a) Find the amplitude.(b) Find the angular frequency.(c) Find the period.arrow_forwardA 0.75-kg mass oscillates according to the equation x(t)=0.85 cos(7.5t), where the position x(t) is measured in meters. What is the maximum acceleration of the mass, in meters per square second?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...
Physics
ISBN:9781133939146
Author:Katz, Debora M.
Publisher:Cengage Learning
Principles of Physics: A Calculus-Based Text
Physics
ISBN:9781133104261
Author:Raymond A. Serway, John W. Jewett
Publisher:Cengage Learning
SIMPLE HARMONIC MOTION (Physics Animation); Author: EarthPen;https://www.youtube.com/watch?v=XjkUcJkGd3Y;License: Standard YouTube License, CC-BY