
Concept explainers
You’ve inherited your great-grandmother’s mantle clock. The clock’s timekeeping is established by a pendulum consisting of a 15.0-cm-long rod and a disk 6.35 cm in diameter. The rod passes through a hole in the disk, and the disk is supported at its bottom by a decorative nut mounted on the bottom portion of the rod, which is threaded: see Fig. 13.38. As shown, the bottom of the disk is 1.92 cm above the bottom of the rod. There are 20.0 threads per cm, meaning that one full turn of the decorative nut moves the disk up or down by 1/20 cm. The clock is beautiful, but it isn’t accurate; you note that it’s losing 1.5 minutes per day. But you realize that the decorative nut is an adjustment mechanism, and you decide to adjust the clock’s timekeeping.
- (a) Should you turn the nut to move the disk up or down?
- (b) How many times should you turn the nut? Note: The disk is massive enough that you can safely neglect the mass of the rod and nut. But you can’t neglect the disk’s size compared with the rod length, so you don’t have a simple pendulum. Furthermore, note that both the effective length of the pendulum and its rotational inertia change as the disk moves up or down the shaft. You can either solve a quadratic or you can use calculus to get an approximate but nevertheless very accurate answer.
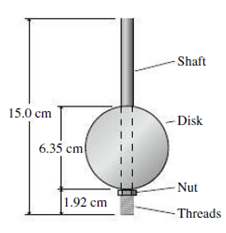
FIGURE 13.38 Problem 85
Want to see the full answer?
Check out a sample textbook solution
Chapter 13 Solutions
Essential University Physics: Volume 1 (3rd Edition)
Additional Science Textbook Solutions
Campbell Essential Biology (7th Edition)
Anatomy & Physiology (6th Edition)
Microbiology: An Introduction
Cosmic Perspective Fundamentals
Human Biology: Concepts and Current Issues (8th Edition)
Introductory Chemistry (6th Edition)
- Correct answer please. I will upvote.arrow_forwardDefine operational amplifierarrow_forwardA bungee jumper plans to bungee jump from a bridge 64.0 m above the ground. He plans to use a uniform elastic cord, tied to a harness around his body, to stop his fall at a point 6.00 m above the water. Model his body as a particle and the cord as having negligible mass and obeying Hooke's law. In a preliminary test he finds that when hanging at rest from a 5.00 m length of the cord, his body weight stretches it by 1.55 m. He will drop from rest at the point where the top end of a longer section of the cord is attached to the bridge. (a) What length of cord should he use? Use subscripts 1 and 2 respectively to represent the 5.00 m test length and the actual jump length. Use Hooke's law F = KAL and the fact that the change in length AL for a given force is proportional the length L (AL = CL), to determine the force constant for the test case and for the jump case. Use conservation of mechanical energy to determine the length of the rope. m (b) What maximum acceleration will he…arrow_forward
- 9 V 300 Ω www 100 Ω 200 Ω www 400 Ω 500 Ω www 600 Ω ww 700 Ω Figure 1: Circuit symbols for a variety of useful circuit elements Problem 04.07 (17 points). Answer the following questions related to the figure below. A What is the equivalent resistance of the network of resistors in the circuit below? B If the battery has an EMF of 9V and is considered as an ideal batter (internal resistance is zero), how much current flows through it in this circuit? C If the 9V EMF battery has an internal resistance of 2 2, would this current be larger or smaller? By how much? D In the ideal battery case, calculate the current through and the voltage across each resistor in the circuit.arrow_forwardhelparrow_forwardIf the block does reach point B, how far up the curved portion of the track does it reach, and if it does not, how far short of point B does the block come to a stop? (Enter your answer in m.)arrow_forward
- Truck suspensions often have "helper springs" that engage at high loads. One such arrangement is a leaf spring with a helper coil spring mounted on the axle, as shown in the figure below. When the main leaf spring is compressed by distance yo, the helper spring engages and then helps to support any additional load. Suppose the leaf spring constant is 5.05 × 105 N/m, the helper spring constant is 3.50 × 105 N/m, and y = 0.500 m. Truck body yo Main leaf spring -"Helper" spring Axle (a) What is the compression of the leaf spring for a load of 6.00 × 105 N? Your response differs from the correct answer by more than 10%. Double check your calculations. m (b) How much work is done in compressing the springs? ☑ Your response differs significantly from the correct answer. Rework your solution from the beginning and check each step carefully. Jarrow_forwardA spring is attached to an inclined plane as shown in the figure. A block of mass m = 2.71 kg is placed on the incline at a distance d = 0.285 m along the incline from the end of the spring. The block is given a quick shove and moves down the incline with an initial speed v = 0.750 m/s. The incline angle is = 20.0°, the spring constant is k = 505 N/m, and we can assume the surface is frictionless. By what distance (in m) is the spring compressed when the block momentarily comes to rest? m m 0 k wwwwarrow_forwardA block of mass m = 2.50 kg situated on an incline at an angle of k=100 N/m www 50.0° is connected to a spring of negligible mass having a spring constant of 100 N/m (Fig. P8.54). The pulley and incline are frictionless. The block is released from rest with the spring initially unstretched. Ө m i (a) How far does it move down the frictionless incline before coming to rest? m (b) What is its acceleration at its lowest point? Magnitude m/s² Direction O up the incline down the inclinearrow_forward
- (a) A 15.0 kg block is released from rest at point A in the figure below. The track is frictionless except for the portion between points B and C, which has a length of 6.00 m. The block travels down the track, hits a spring of force constant 2,100 N/m, and compresses the spring 0.250 m from its equilibrium position before coming to rest momentarily. Determine the coefficient of kinetic friction between the block and the rough surface between points B and C. -A 3.00 m B C -6.00 m i (b) What If? The spring now expands, forcing the block back to the left. Does the block reach point B? Yes No If the block does reach point B, how far up the curved portion of the track does it reach, and if it does not, how far short of point B does the block come to a stop? (Enter your answer in m.) marrow_forwardA ball of mass m = 1.95 kg is released from rest at a height h = 57.0 cm above a light vertical spring of force constant k as in Figure [a] shown below. The ball strikes the top of the spring and compresses it a distance d = 7.80 cm as in Figure [b] shown below. Neglecting any energy losses during the collision, find the following. т m a d T m b i (a) Find the speed of the ball just as it touches the spring. 3.34 m/s (b) Find the force constant of the spring. Your response differs from the correct answer by more than 10%. Double check your calculations. kN/marrow_forwardI need help with questions 1-10 on my solubility curve practice sheet. I tried to my best ability on the answers, however, i believe they are wrong and I would like to know which ones a wrong and just need help figuring it out.arrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning





