
(a)
Interpretation:
The electronic partition function of
Concept introduction:
Statistical
(a)
Answer to Problem 13C.7P
The electronic partition function of
| Temperature | Partition |
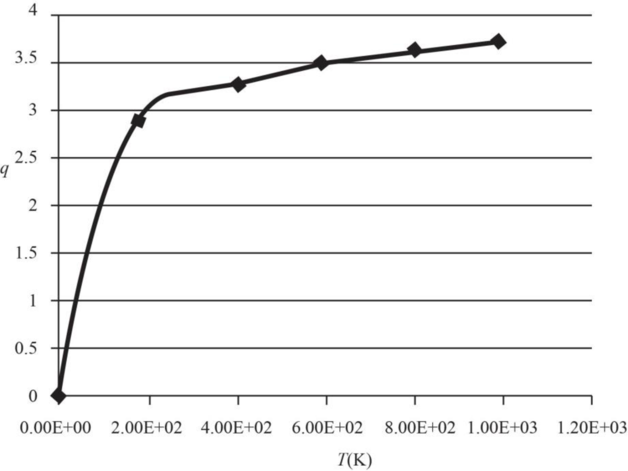
The graph of electronic partition function of
The population of ground and first excited levels of
Explanation of Solution
The partition function in terms of wavenumber is given by the expression as shown below.
Where,
The degeneracy of the ground and first excited electronic level of
The wavenumber of first excited electronic level of
The wavenumber of ground electronic level of
The temperature range is from
The partition function of
Substitute the values of
Substitute the value
Similarly, the partition is calculated for the temperature range from
| Temperature | Partition |
Therefore, the plot electronic partition function of
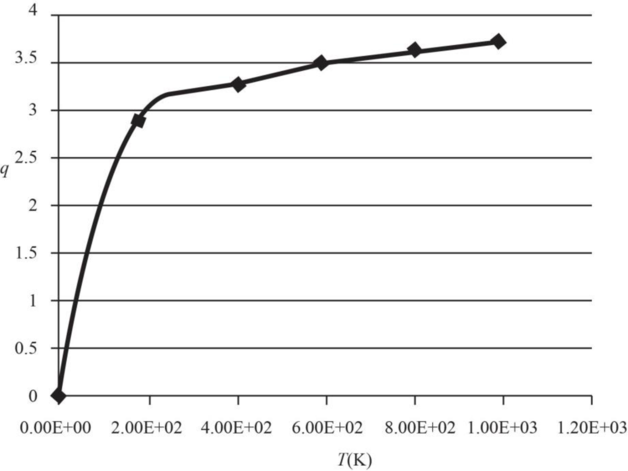
Figure 1
The relative population of ground level of
Substitute the values of
When the total population of the system is
The pollution of first excited level of
Where,
Substitute the value of
Therefore, the population of ground and first excited levels of
(b)
Interpretation:
The mean electronic energy of
Concept introduction:
Refer to part (a).
(b)
Answer to Problem 13C.7P
The mean electronic energy of
Explanation of Solution
The degeneracy of the ground and first excited electronic level of
The wavenumber of first excited electronic level of
The wavenumber of ground electronic level of
The temperature is
The partition function of
Where,
The mean energy,
Substitute the value of
Substitute the value of
Where,
Substitute the values of
The above expression can be further simplified as shown below.
Therefore, the mean electronic energy of
Want to see more full solutions like this?
Chapter 13 Solutions
Atkins' Physical Chemistry
- Identify the missing organic reactants in the following reaction: H+ X + Y OH H+ O O Note: This chemical equation only focuses on the important organic molecules in the reaction. Additional inorganic or small-molecule reactants or products (like H₂O) are not shown. In the drawing area below, draw the skeletal ("line") structures of the missing organic reactants X and Y. You may draw the structures in any arrangement that you like, so long as they aren't touching. Explanation Check Click and drag to start drawing a structure. X G 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Cente ? Earrow_forwardCalculate the solubility of CaF2 in g/L (Kp = 4.0 x 10-8). sparrow_forwardFor the following reaction with excess reagent, predict the product. Be sure your answer accounts for stereochemistry. If multiple stereocenters are formed, be sure to draw all products using appropriate wedges and dashes. 1. EtLi, Et₂O CH₁ ? 2. H₂O*arrow_forward
- Write the systematic name of each organic molecule: structure 요 OH ہو۔ HO OH name X S ☐ ☐arrow_forwardPredict the major products of this organic reaction. If there aren't any products, because nothing will happen, check the box under the drawing area instead. D ㄖˋ ید H No reaction. + 5 H₂O.* Click and drag to start drawing a structure. OH H₂Oarrow_forwardDraw one product of an elimination reaction between the molecules below. Note: There may be several correct answers. You only need to draw one of them. You do not need to draw any of the side products of the reaction 'O 10 + x 也 HO + 义 Click and drag to start drawing a structure.arrow_forward
- What are the angles a and b in the actual molecule of which this is a Lewis structure? H- :0: C=N: b Note for advanced students: give the ideal angles, and don't worry about small differences from the ideal that might be caused by the fact that different electron groups may have slightly different sizes. a = 0° b=0 Xarrow_forwardA student proposes the transformation below in one step of an organic synthesis. There may be one or more products missing from the right-hand side, but there are no reagents missing from the left-hand side. There may also be catalysts, small inorganic reagents, and other important reaction conditions missing from the arrow. • Is the student's transformation possible? If not, check the box under the drawing area. • If the student's transformation is possible, then complete the reaction by adding any missing products to the right-hand side, and adding required catalysts, inorganic reagents, or other important reaction conditions above and below the arrow. • You do not need to balance the reaction, but be sure every important organic reactant or product is shown. + This transformation can't be done in one step. T iarrow_forwardDetermine the structures of the missing organic molecules in the following reaction: H+ O OH H+ + H₂O ☑ ☑ Note: Molecules that share the same letter have the exact same structure. In the drawing area below, draw the skeletal ("line") structure of the missing organic molecule X. Molecule X shows up in multiple steps, but you only have to draw its structure once. Click and drag to start drawing a structure. X § ©arrow_forward
- Table 1.1 Stock Standard Solutions Preparation. The amounts shown should be dissolved in 100 mL. Millipore water. Calculate the corresponding anion concentrations based on the actual weights of the reagents. Anion Amount of reagent (g) Anion Concentration (mg/L) 0.1649 Reagent Chloride NaCl Fluoride NaF 0.2210 Bromide NaBr 0.1288 Nitrate NaNO3 0.1371 Nitrite NaNO2 0.1500 Phosphate KH2PO4 0.1433 Sulfate K2SO4 0.1814arrow_forwardDraw the structure of the pound in the provided CO as a 300-1200 37(2), 11 ( 110, and 2.5 (20arrow_forwardPlease help me with # 4 and 5. Thanks in advance!arrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





