
Interpretation:
Value of
Concept Introduction:
EDTA or ethylenediaminetetraacetic acid is used for titration of majority of metals with help of formation of strong metal complexes in the ratio of
1. Direct titration
2. Back titration
3. Displacement titration
4. Masking
Explanation of Solution
Expression for
Here,
Substitute
At
Expression to calculate
Substitute
When
At
Expression to calculate total volume of solution is as follows:
Substitute
Since EDTA forms strong metal complexes in the ratio of
Expression to calculate excess concentration of
Substitute
Substitute
At
Substitute
Substitute
Substitute
At
Substitute
Substitute
Substitute
At
Formula to calculate molarity of solution is as follows:
Rearrange equation (5) for moles of solute.
Substitute
Substitute
Substitute
Chemical reaction occurs as follows:
Concentration of
Consider change in concentrations of ionic species to be negligible and amount of
Expression to calculate
Substitute
Solve for
Substitute
At
Substitute
Chemical reaction occurs as follows:
Concentration of
Concentration of excess EDTA is calculated as follows:
Rearrange equation (7) for
Substitute
Substitute
At
Substitute
Chemical reaction occurs as follows:
Concentration of
Concentration of excess EDTA is calculated as follows:
Substitute
Substitute
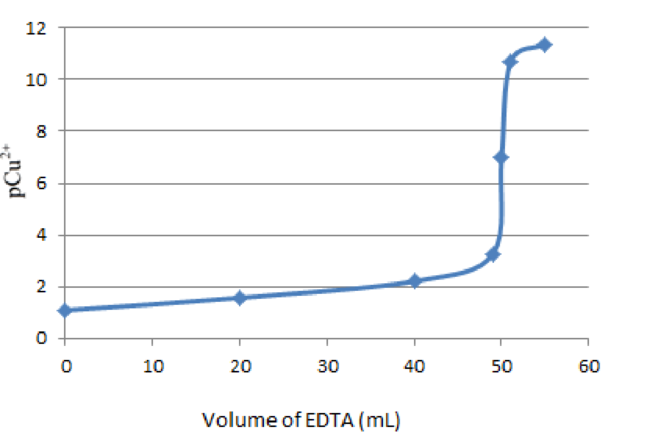
Graph of
Want to see more full solutions like this?
Chapter 13 Solutions
Exploring Chemical Analysis
- Protecting Groups and Carbonyls 6) The synthesis generates allethrolone that exhibits high insect toxicity but low mammalian toxicity. They are used in pet shampoo, human lice shampoo, and industrial sprays for insects and mosquitos. Propose detailed mechanistic steps to generate the allethrolone label the different types of reagents (Grignard, acid/base protonation, acid/base deprotonation, reduction, oxidation, witting, aldol condensation, Robinson annulation, etc.) III + VI HS HS H+ CH,CH,Li III I II IV CI + P(Ph)3 V ༼ Hint: no strong base added VI S VII IX HO VIII -MgBr HgCl2,HgO HO. isomerization aqeuous solution H,SO, ༽༽༤༽༽ X MeOH Hint: enhances selectivity for reaction at the S X ☑arrow_forwardDraw the complete mechanism for the acid-catalyzed hydration of this alkene. esc 田 Explanation Check 1 888 Q A slock Add/Remove step Q F4 F5 F6 A བྲA F7 $ % 5 @ 4 2 3 & 6 87 Click and drag to start drawing a structure. © 2025 McGraw Hill LLC. All Rights Reserved. Terms of Use | Privacy Ce W E R T Y U S D LL G H IK DD 요 F8 F9 F10 F1 * ( 8 9 0 O P J K L Z X C V B N M H He commandarrow_forwardExplanation Check F1 H₂O H₂ Pd 1) MCPBA 2) H3O+ 1) Hg(OAc)2, H₂O 2) NaBH4 OH CI OH OH OH hydration halohydrin formation addition halogenation hydrogenation inhalation hydrogenation hydration ☐ halohydrin formation addition halogenation formation chelation hydrogenation halohydrin formation substitution hydration halogenation addition Ohalohydrin formation subtraction halogenation addition hydrogenation hydration F2 80 F3 σ F4 F5 F6 1 ! 2 # 3 $ 4 % 05 Q W & Å © 2025 McGraw Hill LLC. All Rights Reserved. F7 F8 ( 6 7 8 9 LU E R T Y U A F9arrow_forward
- Show the mechanism steps to obtain the lowerenergy intermediate: *see imagearrow_forwardSoap is made by the previous reaction *see image. The main difference between one soap and another soap isthe length (number of carbons) of the carboxylic acid. However, if a soap irritates your skin, they mostlikely used too much lye.Detergents have the same chemical structure as soaps except for the functional group. Detergentshave sulfate (R-SO4H) and phosphate (R-PO4H2) functional groups. Draw the above carboxylic acidcarbon chain but as the two variants of detergents. *see imagearrow_forwardWhat are the reactions or reagents used? *see imagearrow_forward
- The two pKa values of oxalic acid are 1.25 and 3.81. Why are they not the same value? Show the protontransfer as part of your explanation. *see imagearrow_forwardасть Identify all the bonds that gauche interact with C-OMe in the most stable conformation of the above compound.arrow_forwardPredict the reactants used in the formation of the following compounds using Acid-Catalyzed dehydration reactionarrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





