Chapter 13, Problem 13.1RP

The wood column has a thickness of 4 in. and a width of 6 in. Using the NFPA equations of Sec.13.6 and Eq.13-30, determine the maximum allowable eccentric load P that can be applied. Assume that the column is pinned at both its top and bottom.

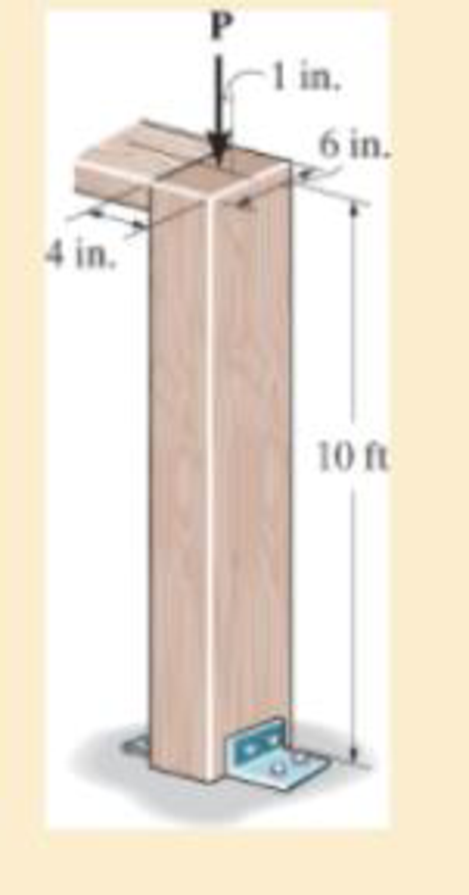
R13−1

To determine

The value of maximum allowable eccentric load on the column.

Answer to Problem 13.1RP

The maximum allowable eccentric load on the column is $\underset{\_}{5.76\text{kip}}$.

Explanation of Solution

Given information:

The load applied on the wooden column is $P$.

The column is pinned at both the ends.

The width of cross-sectional area of the column is $b=6\text{in}\text{.}$

The depth of cross-sectional area of the column is $d=4\text{in}\text{.}$

The length of the column is $L=10\text{ft}$.

Show the expression ofNFPA Equation of Sec 13.6 as follows:

${\left({\sigma }_a\right)}_{\text{allow}}=\left[\frac{540}{{\left(\frac{KL}{d}\right)}^2}\right]\text{ksi,}26<\frac{KL}{r}<50$

Here, ${\left({\sigma }_a\right)}_{\text{allow}}$ is the allowable stress and $\left(\frac{KL}{d}\right)$ is the slenderness ratio.

Show the expression for Equation 13-30 as follows:

${\sigma }_{\max }=\frac{P}{A}+\frac{Mc}{I}$

Here, ${\sigma }_{\max }$ is the maximum compressive stress, P is the load, A is the cross-sectional area, M is the moment, c is the distance between the centroid of member and outer fiber, and I is the moment of inertia.

Calculation:

Calculate the cross-sectional area $\left(A\right)$ of the rectangular column using the relation:

$A=bd$ (1)

Substitute $3\text{in}\text{.}$ for b and $6\text{in}\text{.}$ for d in Equation (1):

$\begin{array}{c}A=4\times 6\\ =24\text{in}{\text{.}}^2\end{array}$

Calculate the moment of inertia using the relation:

$I=\frac{b{d}^3}{12}$ (2)

Substitute $6\text{in}\text{.}$ for b and $4\text{in}\text{.}$ for d in Equation (2):

$\begin{array}{c}I=\frac{6\times 4^3}{12}\\ =32\text{in}{\text{.}}^4\end{array}$

The ends of the column are pinned. Thus, the value of $K=1$.

Calculate the value of $\left(\frac{KL}{d}\right)$ as follows:

Substitute $1$ for K and $3\text{in}\text{.}$ for d.

$\begin{array}{c}\left(\frac{KL}{d}\right)=\left(\frac{1\times 10\text{ft}\times \frac{12\text{in}}{1\text{ft}}}{4\text{in}\text{.}}\right)\\ =\left(\frac{120\text{in}\text{.}}{4\text{in}\text{.}}\right)\\ =30\end{array}$

The value of $\left(\frac{KL}{d}\right)$ lies between 26 and 50.

Show the expression of NFPA Equation of Sec 13.6 as follows:

${\left({\sigma }_a\right)}_{\text{allow}}=\left[\frac{540}{{\left(\frac{KL}{d}\right)}^2}\right]\text{ksi,}26<\frac{KL}{d}<50$ (3)

Here, ${\left({\sigma }_a\right)}_{\text{allow}}$ is the allowable stress and $\left(\frac{KL}{r}\right)$ is the slenderness ratio.

Substitute 30 for $\left(\frac{KL}{d}\right)$ in Equation (3).

$\begin{array}{c}{\left({\sigma }_a\right)}_{\text{allow}}=\left[\frac{540}{{\left(30\right)}^2}\right]\text{ksi}\\ =\left[\frac{540}{900}\right]\text{ksi}\\ =\text{0}\text{.6}\text{ksi}\end{array}$

Show the expression for Equation 13-30 as follows:

$\begin{array}{l}{\sigma }_{\max }=\frac{P}{A}+\frac{Mc}{I}\\ {\sigma }_{\max }=\frac{P}{A}+\frac{\left(Pe\right)c}{I}\end{array}$ (4)

Here, ${\sigma }_{\max }$ is the maximum compressive stress, P is the load, A is the area, M is the moment, c is the distance between the centroid of member and outer fiber, and I is the moment of inertia.

The eccentricity $\left(e\right)$ of the load is $1\text{in}\text{.}$

Calculate the value of c using the relation:

$c=\frac{d}{2}$

Substitute $4\text{in}\text{.}$ for d.

$\begin{array}{c}c=\frac{4}{2}\\ =2\text{in}\text{.}\end{array}$

Substitute $\text{0}\text{.6}\text{ksi}$ for ${\left({\sigma }_a\right)}_{\text{allow}}$, $24\text{in}{\text{.}}^2$ for A,$1\text{in}\text{.}$ for e, $2\text{in}\text{.}$ for c, $32\text{in}{\text{.}}^4$ for I in Equation (4).

$\begin{array}{c}{\sigma }_{\text{allow}}={\sigma }_{\max }\\ 0.6=\frac{P}{24}+\frac{P\times 1\times 2}{32}\\ =\frac{32P+24\times P\times 1\times 2}{24\times 32}\\ =\frac{32P+48P}{24\times 32}\end{array}$

$\begin{array}{c}0.6=\frac{80P}{768}\\ =0.1041P\\ P=\frac{0.6}{0.1041}\\ =5.76\text{kip}\end{array}$

Thus, the maximum allowable eccentric load on the column is $\underset{\_}{5.76\text{kip}}$.