Chapter 12.5, Problem 52SR

To determine

To determine the shaded region the given figure.

Answer to Problem 52SR

  $248$ square millimeters

Explanation of Solution

Given:

  

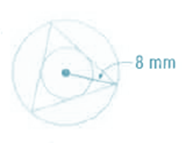
Radius of the outer circle $=8$ millimeters

Formula used:

Area of a circle $=\pi r^2$

where $r$ is the radius of the circle.

Area of an equilateral triangle $=\frac{\sqrt{3}}{4}{a}^2$ , where $a$ is the side of the triangle.

Calculation:

  

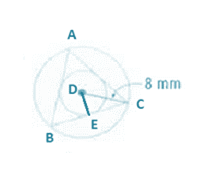
As $\Delta ABC$ is an equilateral triangle, so,

  $\angle ACB={60}^0$

  $\therefore \angle DCE={30}^0$

In $\Delta DCE$ ,

  $DE=$ perpendicular, $EC=$ base, $CD=$ hypotenuse

So,

  $\Rightarrow \cos \theta =\frac{\text{base}}{\text{hypotenuse}}$

  $\Rightarrow \cos {30}^0=\frac{EC}{8}$

  $\Rightarrow \frac{\sqrt{3}}{2}=\frac{EC}{8}$

On cross-multiplying,

  $\Rightarrow EC=\frac{8\sqrt{3}}{2}$

  $\Rightarrow EC=1.43$ millimeters

As $\Delta ABC$ is an equilateral triangle,

So, $BC=2(EC)$

  $\Rightarrow BC=a=2.68$ millimeters

Area of $\Delta ABC=\frac{\sqrt{3}}{4}{a}^2$

Putting the value of a,

  $\Rightarrow \frac{\sqrt{3}}{4}(2.68\times 2.68)$

  $\Rightarrow 3.11$ square millimeters

So, area of $\Delta ABC$

  $=3.11$ square millimeters.

Now,

  $\Rightarrow \sin \theta =\frac{\text{perpendicular}}{\text{hypotenuse}}$

  $\Rightarrow \sin \theta =\frac{DE}{8}$

  $\Rightarrow \frac{1}{2}=\frac{DE}{8}$

On cross-multiplying,

  $\Rightarrow DE=\frac{8}{2}$

  $\Rightarrow DE=4$ millimeters

Area of smaller circle,

Radius $=r=$ 4 millimeters

Area = $\pi r^2$

Putting the value of $r$ ,

  $\Rightarrow 3.14\times 4\times 4$

  $\Rightarrow 50.24$ square millimeters

So, area of small circle $=50.24$ square millimeters.

Now,

Area of outer circle,

  $\Rightarrow \pi R^2$

Putting the value of R,

  $\Rightarrow 3.14\times 8\times 8$

  $\Rightarrow 201$ square millimeters.

So, area of the outer circle $=201$ square millimeters.

Hence, Area of the shaded region = Area of outer circle $-$ Area of the $\Delta ABC$

  $+$ Area of the smaller circle

Now, putting the values,

  $\Rightarrow 201-3.11+50.24$

  $\Rightarrow 248.13$ square millimeters

Conclusion:

Therefore, the area of the shaded region is $248$ square millimeters.