
Concept explainers
Figure 12.20 shows the fool and lower leg of a person standing on the ball of one foot. Three forces act to maintain this equilibrium: the tension force
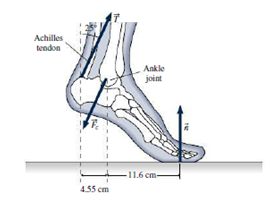
FIGURE 12.20 Problem 28
Want to see the full answer?
Check out a sample textbook solution
Chapter 12 Solutions
Essential University Physics: Volume 1; Mastering Physics with Pearson eText -- ValuePack Access Card -- for Essential University Physics (3rd Edition)
Additional Science Textbook Solutions
Concepts of Genetics (12th Edition)
Chemistry: Structure and Properties (2nd Edition)
College Physics: A Strategic Approach (3rd Edition)
Campbell Biology in Focus (2nd Edition)
Campbell Biology (11th Edition)
Organic Chemistry (8th Edition)
- No chatgpt plsarrow_forwardCar A starts from rest at t = 0 and travels along a straight road with a constant acceleration of 6 ft/s^2 until it reaches a speed of 60ft/s. Afterwards it maintains the speed. Also, when t = 0, car B located 6000 ft down the road is traveling towards A at a constant speed of 80 ft/s. Determine the distance traveled by Car A when they pass each other.Write the solution using pen and draw the graph if needed.arrow_forwardIn the given circuit the charge on the plates of 1 μF capacitor, when 100 V battery is connected to the terminals A and B, will be 2 μF A 1 µF B 3 µFarrow_forward
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed. NOT AI PLSarrow_forward
- The velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardThe velocity of a particle moves along the x-axis and is given by the equation ds/dt = 40 - 3t^2 m/s. Calculate the acceleration at time t=2 s and t=4 s. Calculate also the total displacement at the given interval. Assume at t=0 s=5m.Write the solution using pen and draw the graph if needed.arrow_forwardPlease don't use Chatgpt will upvote and give handwritten solutionarrow_forward
- No chatgpt pls will upvote Already got wrong chatgpt answerarrow_forwardAn electron and a proton are each accelerated through a potential difference of 21.0 million volts. Find the momentum (in MeV/c) and the kinetic energy (in MeV) of each, and compare with the results of using the classical formulas. Momentum (MeV/c) relativistic classical electron proton Kinetic Energy (MeV)arrow_forwardFour capacitors are connected as shown in the figure below. (Let C = 20.0 µF.) (a) Find the equivalent capacitance between points a and b. µF (b) Calculate the charge on each capacitor, taking ΔVab = 14.0 V. 20.0 µF capacitor µC 6.00 µF capacitor µC 3.00 µF capacitor µC capacitor C µCarrow_forward
 College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College
College PhysicsPhysicsISBN:9781938168000Author:Paul Peter Urone, Roger HinrichsPublisher:OpenStax College Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





