Introduction to the Practice of Statistics: w/CrunchIt/EESEE Access Card
8th Edition
ISBN: 9781464158933
Author: David S. Moore, George P. McCabe, Bruce A. Craig
Publisher: W. H. Freeman
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 12, Problem 22E
(a)
To determine
To find: The fitted data and the residuals. Also, generate the
(a)
Expert Solution
Answer to Problem 22E
Solution: The residuals of the provided data is scattered symmetrically above and below the zero and there is no extreme outlier.
Explanation of Solution
Given: The data provided in the Facebook friends study as,
| Friends | Participant | Score |
| 102 | 1 | 3.8 |
| 102 | 2 | 3.6 |
| 102 | 3 | 3.2 |
| 102 | 4 | 2.4 |
| 102 | 5 | 4.8 |
| 102 | 6 | 3.0 |
| 102 | 7 | 4.2 |
| 102 | 8 | 3.6 |
| 102 | 9 | 3.2 |
| 102 | 10 | 3.0 |
| 102 | 11 | 4.8 |
| 102 | 12 | 3.4 |
| 102 | 13 | 4.8 |
| 102 | 14 | 3.0 |
| 102 | 15 | 4.6 |
| 102 | 16 | 2.8 |
| 102 | 17 | 6.0 |
| 102 | 18 | 2.8 |
| 102 | 19 | 5.2 |
| 102 | 20 | 3.2 |
| 102 | 21 | 4.2 |
| 102 | 22 | 2.2 |
| 102 | 23 | 5.0 |
| 102 | 24 | 4.8 |
| 302 | 25 | 5.0 |
| 302 | 26 | 5.2 |
| 302 | 27 | 5.6 |
| 302 | 28 | 2.6 |
| 302 | 29 | 3.8 |
| 302 | 30 | 4.8 |
| 302 | 31 | 5.6 |
| 302 | 32 | 4.8 |
| 302 | 33 | 6.4 |
| 302 | 34 | 4.8 |
| 302 | 35 | 4.4 |
| 302 | 36 | 6.0 |
| 302 | 37 | 3.8 |
| 302 | 38 | 4.8 |
| 302 | 39 | 4.6 |
| 302 | 40 | 6.0 |
| 302 | 41 | 5.0 |
| 302 | 42 | 3.0 |
| 302 | 43 | 4.4 |
| 302 | 44 | 5.4 |
| 302 | 45 | 5.4 |
| 302 | 46 | 4.6 |
| 302 | 47 | 5.6 |
| 302 | 48 | 5.8 |
| 302 | 49 | 4.2 |
| 302 | 50 | 4.8 |
| 302 | 51 | 5.0 |
| 302 | 52 | 5.2 |
| 302 | 53 | 4.2 |
| 302 | 54 | 5.0 |
| 302 | 55 | 5.8 |
| 302 | 56 | 5.6 |
| 302 | 57 | 3.8 |
| 502 | 58 | 4.6 |
| 502 | 59 | 4.0 |
| 502 | 60 | 4.8 |
| 502 | 61 | 3.0 |
| 502 | 62 | 2.0 |
| 502 | 63 | 5.8 |
| 502 | 64 | 5.6 |
| 502 | 65 | 4.4 |
| 502 | 66 | 4.4 |
| 502 | 67 | 5.6 |
| 502 | 68 | 4.6 |
| 502 | 69 | 5.6 |
| 502 | 70 | 3.0 |
| 502 | 71 | 5.6 |
| 502 | 72 | 3.6 |
| 502 | 73 | 6.8 |
| 502 | 74 | 3.2 |
| 502 | 75 | 4.8 |
| 502 | 76 | 4.6 |
| 502 | 77 | 5.4 |
| 502 | 78 | 4.8 |
| 502 | 79 | 4.8 |
| 502 | 80 | 5.4 |
| 502 | 81 | 3.6 |
| 502 | 82 | 4.8 |
| 502 | 83 | 3.8 |
| 702 | 84 | 3.2 |
| 702 | 85 | 3.6 |
| 702 | 86 | 5.8 |
| 702 | 87 | 1.2 |
| 702 | 88 | 3.8 |
| 702 | 89 | 5.4 |
| 702 | 90 | 3.6 |
| 702 | 91 | 3.4 |
| 702 | 92 | 5.0 |
| 702 | 93 | 5.2 |
| 702 | 94 | 3.6 |
| 702 | 95 | 2.6 |
| 702 | 96 | 7.0 |
| 702 | 97 | 4.4 |
| 702 | 98 | 4.8 |
| 702 | 99 | 5.2 |
| 702 | 100 | 5.4 |
| 702 | 101 | 3.6 |
| 702 | 102 | 1.0 |
| 702 | 103 | 5.0 |
| 702 | 104 | 5.0 |
| 702 | 105 | 6.0 |
| 702 | 106 | 4.2 |
| 702 | 107 | 5.8 |
| 702 | 108 | 3.2 |
| 702 | 109 | 5.4 |
| 702 | 110 | 6.4 |
| 702 | 111 | 4.4 |
| 702 | 112 | 3.0 |
| 702 | 113 | 6.0 |
| 902 | 114 | 4.2 |
| 902 | 115 | 4.6 |
| 902 | 116 | 3.0 |
| 902 | 117 | 2.6 |
| 902 | 118 | 5.2 |
| 902 | 119 | 5.2 |
| 902 | 120 | 1.6 |
| 902 | 121 | 5.0 |
| 902 | 122 | 4.4 |
| 902 | 123 | 5.0 |
| 902 | 124 | 3.6 |
| 902 | 125 | 4.2 |
| 902 | 126 | 5.0 |
| 902 | 127 | 3.4 |
| 902 | 128 | 3.6 |
| 902 | 129 | 5.0 |
| 902 | 130 | 3.2 |
| 902 | 131 | 2.4 |
| 902 | 132 | 4.8 |
| 902 | 133 | 3.6 |
| 902 | 134 | 4.2 |
Calculation:
Use Minitab to find the residuals, of the provided data as below:
Step1: Enter the provided data in the worksheet.
Step2: Select stat >ANOVA>one-way analysis of variance.
Step3: Select Score in the Response and Friends in the Factor.
Step4: Click on Graphs and select the Residual verses fitand then press OK.
Step5: Select Store residual and Store fit.
Step6: Press OK.
Theobtained output of fitted data and the residual stored in the data file as below:
| Friends | Participant | Score | RESI1 | FITS1 |
| 102 | 1 | 3.8 | -0.01667 | 3.816667 |
| 102 | 2 | 3.6 | -0.21667 | 3.816667 |
| 102 | 3 | 3.2 | -0.61667 | 3.816667 |
| 102 | 4 | 2.4 | -1.41667 | 3.816667 |
| 102 | 5 | 4.8 | 0.983333 | 3.816667 |
| 102 | 6 | 3.0 | -0.81667 | 3.816667 |
| 102 | 7 | 4.2 | 0.383333 | 3.816667 |
| 102 | 8 | 3.6 | -0.21667 | 3.816667 |
| 102 | 9 | 3.2 | -0.61667 | 3.816667 |
| 102 | 10 | 3.0 | -0.81667 | 3.816667 |
| 102 | 11 | 4.8 | 0.983333 | 3.816667 |
| 102 | 12 | 3.4 | -0.41667 | 3.816667 |
| 102 | 13 | 4.8 | 0.983333 | 3.816667 |
| 102 | 14 | 3.0 | -0.81667 | 3.816667 |
| 102 | 15 | 4.6 | 0.783333 | 3.816667 |
| 102 | 16 | 2.8 | -1.01667 | 3.816667 |
| 102 | 17 | 6.0 | 2.183333 | 3.816667 |
| 102 | 18 | 2.8 | -1.01667 | 3.816667 |
| 102 | 19 | 5.2 | 1.383333 | 3.816667 |
| 102 | 20 | 3.2 | -0.61667 | 3.816667 |
| 102 | 21 | 4.2 | 0.383333 | 3.816667 |
| 102 | 22 | 2.2 | -1.61667 | 3.816667 |
| 102 | 23 | 5.0 | 1.183333 | 3.816667 |
| 102 | 24 | 4.8 | 0.983333 | 3.816667 |
| 302 | 25 | 5.0 | 0.121212 | 4.878788 |
| 302 | 26 | 5.2 | 0.321212 | 4.878788 |
| 302 | 27 | 5.6 | 0.721212 | 4.878788 |
| 302 | 28 | 2.6 | -2.27879 | 4.878788 |
| 302 | 29 | 3.8 | -1.07879 | 4.878788 |
| 302 | 30 | 4.8 | -0.07879 | 4.878788 |
| 302 | 31 | 5.6 | 0.721212 | 4.878788 |
| 302 | 32 | 4.8 | -0.07879 | 4.878788 |
| 302 | 33 | 6.4 | 1.521212 | 4.878788 |
| 302 | 34 | 4.8 | -0.07879 | 4.878788 |
| 302 | 35 | 4.4 | -0.47879 | 4.878788 |
| 302 | 36 | 6.0 | 1.121212 | 4.878788 |
| 302 | 37 | 3.8 | -1.07879 | 4.878788 |
| 302 | 38 | 4.8 | -0.07879 | 4.878788 |
| 302 | 39 | 4.6 | -0.27879 | 4.878788 |
| 302 | 40 | 6.0 | 1.121212 | 4.878788 |
| 302 | 41 | 5.0 | 0.121212 | 4.878788 |
| 302 | 42 | 3.0 | -1.87879 | 4.878788 |
| 302 | 43 | 4.4 | -0.47879 | 4.878788 |
| 302 | 44 | 5.4 | 0.521212 | 4.878788 |
| 302 | 45 | 5.4 | 0.521212 | 4.878788 |
| 302 | 46 | 4.6 | -0.27879 | 4.878788 |
| 302 | 47 | 5.6 | 0.721212 | 4.878788 |
| 302 | 48 | 5.8 | 0.921212 | 4.878788 |
| 302 | 49 | 4.2 | -0.67879 | 4.878788 |
| 302 | 50 | 4.8 | -0.07879 | 4.878788 |
| 302 | 51 | 5.0 | 0.121212 | 4.878788 |
| 302 | 52 | 5.2 | 0.321212 | 4.878788 |
| 302 | 53 | 4.2 | -0.67879 | 4.878788 |
| 302 | 54 | 5.0 | 0.121212 | 4.878788 |
| 302 | 55 | 5.8 | 0.921212 | 4.878788 |
| 302 | 56 | 5.6 | 0.721212 | 4.878788 |
| 302 | 57 | 3.8 | -1.07879 | 4.878788 |
| 502 | 58 | 4.6 | 0.038462 | 4.561538 |
| 502 | 59 | 4.0 | -0.56154 | 4.561538 |
| 502 | 60 | 4.8 | 0.238462 | 4.561538 |
| 502 | 61 | 3.0 | -1.56154 | 4.561538 |
| 502 | 62 | 2.0 | -2.56154 | 4.561538 |
| 502 | 63 | 5.8 | 1.238462 | 4.561538 |
| 502 | 64 | 5.6 | 1.038462 | 4.561538 |
| 502 | 65 | 4.4 | -0.16154 | 4.561538 |
| 502 | 66 | 4.4 | -0.16154 | 4.561538 |
| 502 | 67 | 5.6 | 1.038462 | 4.561538 |
| 502 | 68 | 4.6 | 0.038462 | 4.561538 |
| 502 | 69 | 5.6 | 1.038462 | 4.561538 |
| 502 | 70 | 3.0 | -1.56154 | 4.561538 |
| 502 | 71 | 5.6 | 1.038462 | 4.561538 |
| 502 | 72 | 3.6 | -0.96154 | 4.561538 |
| 502 | 73 | 6.8 | 2.238462 | 4.561538 |
| 502 | 74 | 3.2 | -1.36154 | 4.561538 |
| 502 | 75 | 4.8 | 0.238462 | 4.561538 |
| 502 | 76 | 4.6 | 0.038462 | 4.561538 |
| 502 | 77 | 5.4 | 0.838462 | 4.561538 |
| 502 | 78 | 4.8 | 0.238462 | 4.561538 |
| 502 | 79 | 4.8 | 0.238462 | 4.561538 |
| 502 | 80 | 5.4 | 0.838462 | 4.561538 |
| 502 | 81 | 3.6 | -0.96154 | 4.561538 |
| 502 | 82 | 4.8 | 0.238462 | 4.561538 |
| 502 | 83 | 3.8 | -0.76154 | 4.561538 |
| 702 | 84 | 3.2 | -1.20667 | 4.406667 |
| 702 | 85 | 3.6 | -0.80667 | 4.406667 |
| 702 | 86 | 5.8 | 1.393333 | 4.406667 |
| 702 | 87 | 1.2 | -3.20667 | 4.406667 |
| 702 | 88 | 3.8 | -0.60667 | 4.406667 |
| 702 | 89 | 5.4 | 0.993333 | 4.406667 |
| 702 | 90 | 3.6 | -0.80667 | 4.406667 |
| 702 | 91 | 3.4 | -1.00667 | 4.406667 |
| 702 | 92 | 5.0 | 0.593333 | 4.406667 |
| 702 | 93 | 5.2 | 0.793333 | 4.406667 |
| 702 | 94 | 3.6 | -0.80667 | 4.406667 |
| 702 | 95 | 2.6 | -1.80667 | 4.406667 |
| 702 | 96 | 7.0 | 2.593333 | 4.406667 |
| 702 | 97 | 4.4 | -0.00667 | 4.406667 |
| 702 | 98 | 4.8 | 0.393333 | 4.406667 |
| 702 | 99 | 5.2 | 0.793333 | 4.406667 |
| 702 | 100 | 5.4 | 0.993333 | 4.406667 |
| 702 | 101 | 3.6 | -0.80667 | 4.406667 |
| 702 | 102 | 1.0 | -3.40667 | 4.406667 |
| 702 | 103 | 5.0 | 0.593333 | 4.406667 |
| 702 | 104 | 5.0 | 0.593333 | 4.406667 |
| 702 | 105 | 6.0 | 1.593333 | 4.406667 |
| 702 | 106 | 4.2 | -0.20667 | 4.406667 |
| 702 | 107 | 5.8 | 1.393333 | 4.406667 |
| 702 | 108 | 3.2 | -1.20667 | 4.406667 |
| 702 | 109 | 5.4 | 0.993333 | 4.406667 |
| 702 | 110 | 6.4 | 1.993333 | 4.406667 |
| 702 | 111 | 4.4 | -0.00667 | 4.406667 |
| 702 | 112 | 3.0 | -1.40667 | 4.406667 |
| 702 | 113 | 6.0 | 1.593333 | 4.406667 |
| 902 | 114 | 4.2 | 0.209524 | 3.990476 |
| 902 | 115 | 4.6 | 0.609524 | 3.990476 |
| 902 | 116 | 3.0 | -0.99048 | 3.990476 |
| 902 | 117 | 2.6 | -1.39048 | 3.990476 |
| 902 | 118 | 5.2 | 1.209524 | 3.990476 |
| 902 | 119 | 5.2 | 1.209524 | 3.990476 |
| 902 | 120 | 1.6 | -2.39048 | 3.990476 |
| 902 | 121 | 5.0 | 1.009524 | 3.990476 |
| 902 | 122 | 4.4 | 0.409524 | 3.990476 |
| 902 | 123 | 5.0 | 1.009524 | 3.990476 |
| 902 | 124 | 3.6 | -0.39048 | 3.990476 |
| 902 | 125 | 4.2 | 0.209524 | 3.990476 |
| 902 | 126 | 5.0 | 1.009524 | 3.990476 |
| 902 | 127 | 3.4 | -0.59048 | 3.990476 |
| 902 | 128 | 3.6 | -0.39048 | 3.990476 |
| 902 | 129 | 5.0 | 1.009524 | 3.990476 |
| 902 | 130 | 3.2 | -0.79048 | 3.990476 |
| 902 | 131 | 2.4 | -1.59048 | 3.990476 |
| 902 | 132 | 4.8 | 0.809524 | 3.990476 |
| 902 | 133 | 3.6 | -0.39048 | 3.990476 |
| 902 | 134 | 4.2 | 0.209524 | 3.990476 |
The scatterplot of the residuals versus the group variable is,
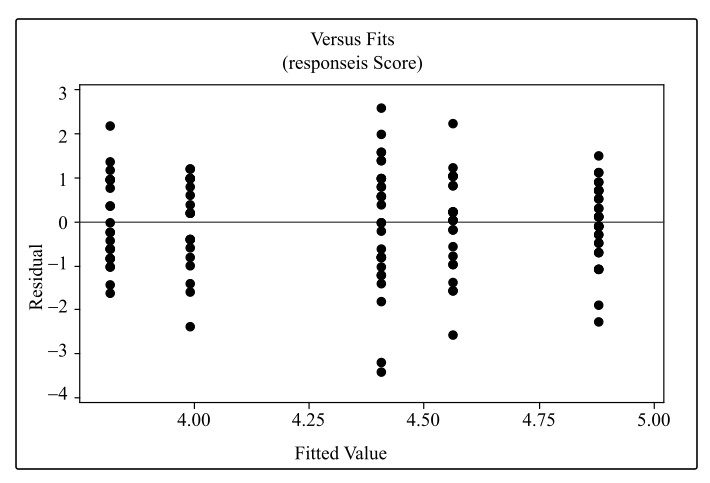
Interpretation: From the above graph, it is observed that the scatter plot of the residuals is symmetrically scattered below and above the zero and there are two outliers below the zero but these are not the extreme outliers.
(b)
To determine
Whether the spread of the residual of each group is relatively equal or not.
(b)
Expert Solution
Answer to Problem 22E
Solution: Yes, the spread of the residual of each group is relatively equal.
Explanation of Solution
From the scatterplot of the residuals versus the group variables in part (a), it is observed that the residuals are symmetrically scattered below and above the zero. It implies that the spread of the residual of each group is relatively equal.
(c)
To determine
To graph: The Normal quantile plot of the residuals obtained in part (a) and identify whether it is normal or not.
(c)
Expert Solution
Explanation of Solution
Graph:
Use Minitab to graph the Normal quantile plot as below:
Step1: Enter the provided data in the worksheet.
Step2: Select stat> ANOVA>one-way analysis of variance.
Step3: Select Score in the Response and Friends in the Factor.
Step4: Click on Graphs and select the Normal plot of residuals and then press OK.
Step5: Press OK.
The obtained graph is,
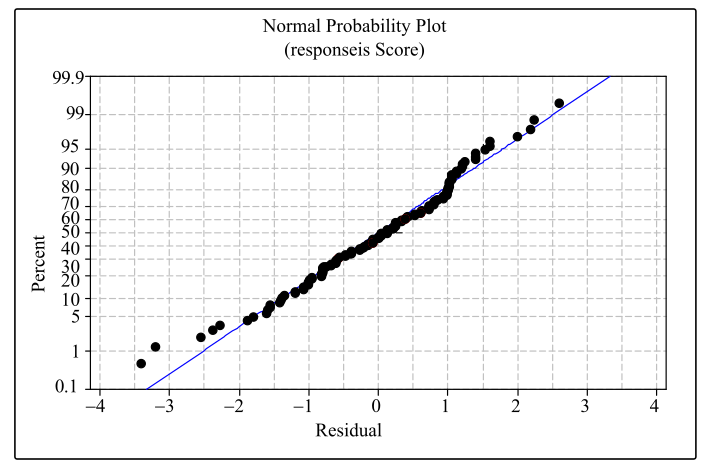
Interpretation: From the obtained graph, it is observed that the normal quantile plot is nearly fitted to the line. Hence, the residual is approximately normal.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
PEER REPLY 1:
Choose a classmate's Main Post and review their decision making process.
1. Choose a risk level for each of the states of nature (assign a probability
value to each).
2. Explain why each risk level is chosen.
3. Which alternative do you believe would be the best based on the maximum
EMV?
4. Do you feel determining the expected value with perfect information
(EVWPI) is worthwhile in this situation? Why or why not?
Questions
An insurance company's cumulative incurred claims for the last 5 accident years are given
in the following table:
Development Year
Accident Year 0
2018
1 2 3 4
245 267 274 289 292
2019
255 276 288 294
2020
265 283 292
2021
263 278
2022
271
It can be assumed that claims are fully run off after 4 years. The premiums received for
each year are:
Accident Year Premium
2018
306
2019
312
2020
318
2021
326
2022
330
You do not need to make any allowance for inflation.
1. (a) Calculate the reserve at the end of 2022 using the basic chain ladder method.
(b) Calculate the reserve at the end of 2022 using the Bornhuetter-Ferguson method.
2. Comment on the differences in the reserves produced by the methods in Part 1.
You are provided with data that includes all 50 states of the United States. Your task is to draw a sample of: o 20 States using Random Sampling (2 points: 1 for random number generation; 1 for random sample) o 10 States using Systematic Sampling (4 points: 1 for random numbers generation; 1 for random sample different from the previous answer; 1 for correct K value calculation table; 1 for correct sample drawn by using systematic sampling) (For systematic sampling, do not use the original data directly. Instead, first randomize the data, and then use the randomized dataset to draw your sample. Furthermore, do not use the random list previously generated, instead, generate a new random sample for this part. For more details, please see the snapshot provided at the end.) Upload a Microsoft Excel file with two separate sheets. One sheet provides random sampling while the other provides systematic sampling. Excel snapshots that can help you in organizing columns are provided on the next…
Chapter 12 Solutions
Introduction to the Practice of Statistics: w/CrunchIt/EESEE Access Card
Ch. 12.1 - Prob. 1UYKCh. 12.1 - Prob. 2UYKCh. 12.1 - Prob. 3UYKCh. 12.1 - Prob. 5UYKCh. 12.1 - Prob. 6UYKCh. 12.1 - Prob. 4UYKCh. 12.2 - Prob. 7UYKCh. 12.2 - Prob. 8UYKCh. 12 - Prob. 9ECh. 12 - Prob. 10E
Ch. 12 - Prob. 11ECh. 12 - Prob. 12ECh. 12 - Prob. 13ECh. 12 - Prob. 14ECh. 12 - Prob. 15ECh. 12 - Prob. 16ECh. 12 - Prob. 17ECh. 12 - Prob. 18ECh. 12 - Prob. 39ECh. 12 - Prob. 19ECh. 12 - Prob. 43ECh. 12 - Prob. 41ECh. 12 - Prob. 42ECh. 12 - Prob. 49ECh. 12 - Prob. 20ECh. 12 - Prob. 21ECh. 12 - Prob. 28ECh. 12 - Prob. 29ECh. 12 - Prob. 30ECh. 12 - Prob. 35ECh. 12 - Prob. 36ECh. 12 - Prob. 23ECh. 12 - Prob. 24ECh. 12 - Prob. 25ECh. 12 - Prob. 26ECh. 12 - Prob. 31ECh. 12 - Prob. 32ECh. 12 - Prob. 33ECh. 12 - Prob. 34ECh. 12 - Prob. 37ECh. 12 - Prob. 38ECh. 12 - Prob. 27ECh. 12 - Prob. 40ECh. 12 - Prob. 45ECh. 12 - Prob. 46ECh. 12 - Prob. 47ECh. 12 - Prob. 48ECh. 12 - Prob. 50ECh. 12 - Prob. 51ECh. 12 - Prob. 52ECh. 12 - Prob. 53ECh. 12 - Prob. 54ECh. 12 - Prob. 55ECh. 12 - Prob. 56ECh. 12 - Prob. 57ECh. 12 - Prob. 58ECh. 12 - Prob. 59ECh. 12 - Prob. 60ECh. 12 - Prob. 63ECh. 12 - Prob. 22ECh. 12 - Prob. 67ECh. 12 - Prob. 68ECh. 12 - Prob. 69ECh. 12 - Prob. 44ECh. 12 - Prob. 61ECh. 12 - Prob. 62ECh. 12 - Prob. 64ECh. 12 - Prob. 65ECh. 12 - Prob. 66E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, statistics and related others by exploring similar questions and additional content below.Similar questions
- The population mean and standard deviation are given below. Find the required probability and determine whether the given sample mean would be considered unusual. For a sample of n = 65, find the probability of a sample mean being greater than 225 if μ = 224 and σ = 3.5. For a sample of n = 65, the probability of a sample mean being greater than 225 if μ=224 and σ = 3.5 is 0.0102 (Round to four decimal places as needed.)arrow_forward***Please do not just simply copy and paste the other solution for this problem posted on bartleby as that solution does not have all of the parts completed for this problem. Please answer this I will leave a like on the problem. The data needed to answer this question is given in the following link (file is on view only so if you would like to make a copy to make it easier for yourself feel free to do so) https://docs.google.com/spreadsheets/d/1aV5rsxdNjHnkeTkm5VqHzBXZgW-Ptbs3vqwk0SYiQPo/edit?usp=sharingarrow_forwardThe data needed to answer this question is given in the following link (file is on view only so if you would like to make a copy to make it easier for yourself feel free to do so) https://docs.google.com/spreadsheets/d/1aV5rsxdNjHnkeTkm5VqHzBXZgW-Ptbs3vqwk0SYiQPo/edit?usp=sharingarrow_forward
- The following relates to Problems 4 and 5. Christchurch, New Zealand experienced a major earthquake on February 22, 2011. It destroyed 100,000 homes. Data were collected on a sample of 300 damaged homes. These data are saved in the file called CIEG315 Homework 4 data.xlsx, which is available on Canvas under Files. A subset of the data is shown in the accompanying table. Two of the variables are qualitative in nature: Wall construction and roof construction. Two of the variables are quantitative: (1) Peak ground acceleration (PGA), a measure of the intensity of ground shaking that the home experienced in the earthquake (in units of acceleration of gravity, g); (2) Damage, which indicates the amount of damage experienced in the earthquake in New Zealand dollars; and (3) Building value, the pre-earthquake value of the home in New Zealand dollars. PGA (g) Damage (NZ$) Building Value (NZ$) Wall Construction Roof Construction Property ID 1 0.645 2 0.101 141,416 2,826 253,000 B 305,000 B T 3…arrow_forwardRose Par posted Apr 5, 2025 9:01 PM Subscribe To: Store Owner From: Rose Par, Manager Subject: Decision About Selling Custom Flower Bouquets Date: April 5, 2025 Our shop, which prides itself on selling handmade gifts and cultural items, has recently received inquiries from customers about the availability of fresh flower bouquets for special occasions. This has prompted me to consider whether we should introduce custom flower bouquets in our shop. We need to decide whether to start offering this new product. There are three options: provide a complete selection of custom bouquets for events like birthdays and anniversaries, start small with just a few ready-made flower arrangements, or do not add flowers. There are also three possible outcomes. First, we might see high demand, and the bouquets could sell quickly. Second, we might have medium demand, with a few sold each week. Third, there might be low demand, and the flowers may not sell well, possibly going to waste. These outcomes…arrow_forwardConsider the state space model X₁ = §Xt−1 + Wt, Yt = AX+Vt, where Xt Є R4 and Y E R². Suppose we know the covariance matrices for Wt and Vt. How many unknown parameters are there in the model?arrow_forward
- Business Discussarrow_forwardYou want to obtain a sample to estimate the proportion of a population that possess a particular genetic marker. Based on previous evidence, you believe approximately p∗=11% of the population have the genetic marker. You would like to be 90% confident that your estimate is within 0.5% of the true population proportion. How large of a sample size is required?n = (Wrong: 10,603) Do not round mid-calculation. However, you may use a critical value accurate to three decimal places.arrow_forward2. [20] Let {X1,..., Xn} be a random sample from Ber(p), where p = (0, 1). Consider two estimators of the parameter p: 1 p=X_and_p= n+2 (x+1). For each of p and p, find the bias and MSE.arrow_forward
- 1. [20] The joint PDF of RVs X and Y is given by xe-(z+y), r>0, y > 0, fx,y(x, y) = 0, otherwise. (a) Find P(0X≤1, 1arrow_forward4. [20] Let {X1,..., X} be a random sample from a continuous distribution with PDF f(x; 0) = { Axe 5 0, x > 0, otherwise. where > 0 is an unknown parameter. Let {x1,...,xn} be an observed sample. (a) Find the value of c in the PDF. (b) Find the likelihood function of 0. (c) Find the MLE, Ô, of 0. (d) Find the bias and MSE of 0.arrow_forward3. [20] Let {X1,..., Xn} be a random sample from a binomial distribution Bin(30, p), where p (0, 1) is unknown. Let {x1,...,xn} be an observed sample. (a) Find the likelihood function of p. (b) Find the MLE, p, of p. (c) Find the bias and MSE of p.arrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_ios
Recommended textbooks for you
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Correlation Vs Regression: Difference Between them with definition & Comparison Chart; Author: Key Differences;https://www.youtube.com/watch?v=Ou2QGSJVd0U;License: Standard YouTube License, CC-BY
Correlation and Regression: Concepts with Illustrative examples; Author: LEARN & APPLY : Lean and Six Sigma;https://www.youtube.com/watch?v=xTpHD5WLuoA;License: Standard YouTube License, CC-BY