
Concept explainers
(a)
To calculate: The concentration of carbon mono-oxide at steady state in each room, for the system provided as shown below:
(a)
Answer to Problem 20P
Solution: The concentrations of carbon mono-oxide
and
Explanation of Solution
Given Information:
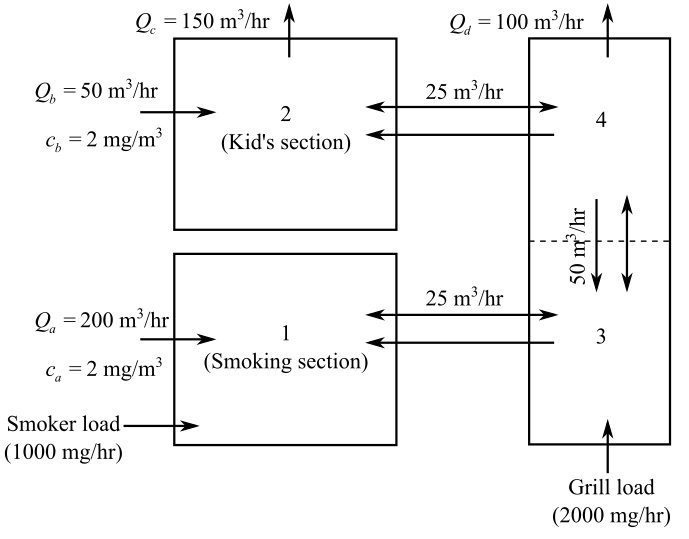
The air flow through the room with proper description is provided as follows:

Also, for the smoking section (room 1) the balance can be written as follows:
Formula used:
Write system of linear equations in matrix form.
And,
The term
, represent the variable matrix,
Calculation:
Consider the provided figure:
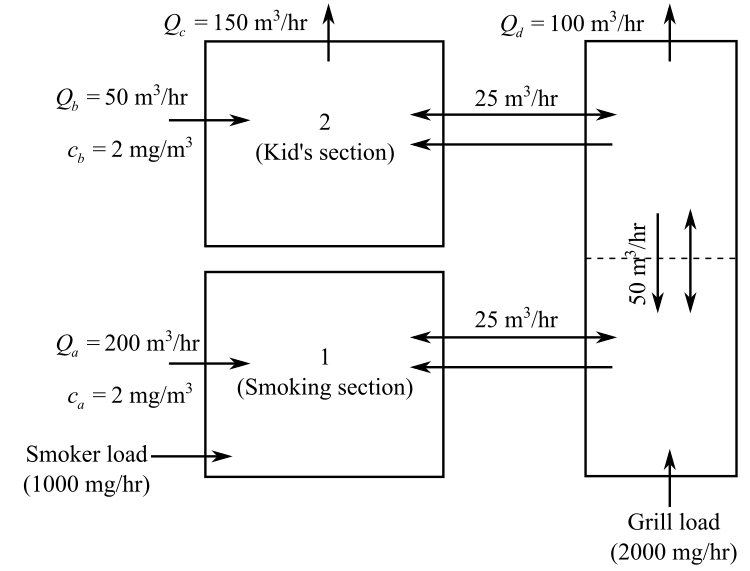
Here, Q is the flow rate in cubic meter per hour and c is the concentration in milligrams cubic per meter.
Taking Smoking section into consideration the mass balance equation for room 1 is as follows:
Substitute the known values:
Taking Kid’s section into consideration the mass balance equation for room 2 is as follows:
Substitute the known values and solve:
The mass balance equation for room 3 is as follows:
Substitute the known values and solve:
The mass balance equation for room 4 is as follows:
Substitute the known values and solve;
Consider all the linear equation obtained above.
The system of equations is written in augmented form as shown below:
Here, the coefficient matrix A is:
The column matrix X is,
And
The column matrix D is:
Substitute the values in the augmented form of the equation:
To solve the equation use MATLAB, follow the following seeps to obtained the result: 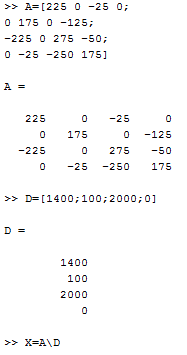
Once these details are added in the MATLAB “cmd” press enter and the result is obtained as follows:

Hence, the concentration matrix for carbon mono-oxide is as follows:
Therefore, the concentrations
(b)
To calculate: The percentage of carbon mono-oxide due to (i) the smokers, (ii) the grill and the air in the intake vents.
(b)
Answer to Problem 20P
Solution: The percent of the carbon mon-oxide in the kids’ section due to smokers, grills, and air intake vents is
and
Explanation of Solution
Given Information:
The air flow through the room with proper description is provided as follows:

Also, for the smoking section (room 1) the balance can be written as follows:
Calculation:
Rewrite all the linear equation obtained in part (a).
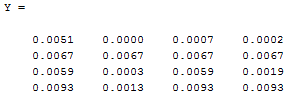
Open MATLAB and enter values as shown below,

Once, you press enter after adding these all in the matlab “cmd” the result is obtained as:
(i)
Follow the following procedure to obtain the value of the carbon mono-oxide concentration in kid’s section.
The concentration of the carbon mono-oxide in the kid’s section is:
Substitute
Carbon monoxide percentage in the kids’ section due to smokers is as follows,
The concentration of the carbon mono-oxide in the kid’s section due to grill is:
Substitute
Carbon monoxide percentage in the kids’ section due to grill is as follows,
(iii)
The concentration of the carbon mono-oxide in the kid’s section due to air intake vents is:
Substitute the known values:
Carbon monoxide percentage in the kids’ section due to air intake vents is:
Hence, the percent of the carbon monoxide in the kids’ section due to smokers, grills, and air intake vents is
(c)
To calculate: The increase in concentration in the kid’s section by using matrix inverse if the smokers and grill loads are increased to
(c)
Answer to Problem 20P
Solution: The increase in the kid’s section is
Explanation of Solution
Given Information:
The air flow through the room with proper description is provided as follows:

Also, for the smoking section (room 1) the balance can be written as follows:
Calculation:
The smoker and grill loads are increased to 2000 and 5000
Therefore, increase in concentration of carbon mono-oxide after increase of smoker loads is:
Substitute
Therefore, increase in concentration of carbon mono-oxide after increase of grill load is:
Substitute
Therefore, increase in the concentration of the carbon mon-oxide in the kid’s section is:
The incereases in concetration is
(d)
To calculate: The change in the concentration in the kid’s section if the mixing between area 2 and 4 is decreases to
(d)
Answer to Problem 20P
Solution: There won’t be any changes in concertation in kid’s section.
Explanation of Solution
Given Information:
The air flow through the room with proper description is provided as follows:

Also, for the smoking section (room 1) the balance can be written as follows:
Formula used:
Write system of linear equations in matrix form.
And,
The term
, represent the variable matrix,
Calculation:
The mixing between areas 2 and 4 is decreased to
Therefore, the value of
The balance equation for room 1 is written as follows:
Substitute the known values;
The balance equation for room 2 is written as follows:
Substitute the known values and solve:
The balance equation for room 3 is written as follows:
Substitute the known values and solve:
The balance equation for room 4 is written as follows:
Substitute the known values and solve.
Rewrite all the equations obtained by applying mass balance equation.
Rewrite the linear equations system in augmented form as shown below.
Here, the coefficient matrix A is,
The column matrix X is:
The column matrix D is;
Substitute the value of the matrices.
Add the following code into MATLAB “cmd”.
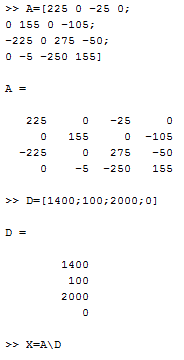
Press enter to get the result.

Hence, the equivalent concentration matrix is:
Therefore, the concentration in the kids’ area is:
Therefore, there won’t be any changes in the concentration of the kid’s room area.
Want to see more full solutions like this?
Chapter 12 Solutions
Numerical Methods for Engineers
- The 120 kg wheel has a radius of gyration of 0.7 m. A force P with a magnitude of 50 N is applied at the edge of the wheel as seen in the diagram. The coefficient of static friction is 0.3, and the coefficient of kinetic friction is 0.25. Find the acceleration and angular acceleration of the wheel.arrow_forwardAuto Controls Using MATLAB , find the magnitude and phase plot of the compensators NO COPIED SOLUTIONSarrow_forward4-81 The corner shown in Figure P4-81 is initially uniform at 300°C and then suddenly exposed to a convection environment at 50°C with h 60 W/m². °C. Assume the = 2 solid has the properties of fireclay brick. Examine nodes 1, 2, 3, 4, and 5 and deter- mine the maximum time increment which may be used for a transient numerical calculation. Figure P4-81 1 2 3 4 1 cm 5 6 1 cm 2 cm h, T + 2 cmarrow_forward
- Auto Controls A union feedback control system has the following open loop transfer function where k>0 is a variable proportional gain i. for K = 1 , derive the exact magnitude and phase expressions of G(jw). ii) for K = 1 , identify the gaincross-over frequency (Wgc) [where IG(jo))| 1] and phase cross-overfrequency [where <G(jw) = - 180]. You can use MATLAB command "margin" to obtain there quantities. iii) Calculate gain margin (in dB) and phase margin (in degrees) ·State whether the closed-loop is stable for K = 1 and briefly justify your answer based on the margin . (Gain marginPhase margin) iv. what happens to the gain margin and Phase margin when you increase the value of K?you You can use for loop in MATLAB to check that.Helpful matlab commands : if, bode, margin, rlocus NO COPIED SOLUTIONSarrow_forwardAuto Controls Hand sketch the root Focus of the following transfer function How many asymptotes are there ?what are the angles of the asymptotes?Does the system remain stable for all values of K NO COPIED SOLUTIONSarrow_forward-400" 150" in Datum 80" 90" -280"arrow_forward
- 7) Please draw the front, top and side view for the following object. Please cross this line outarrow_forwardA 10-kg box is pulled along P,Na rough surface by a force P, as shown in thefigure. The pulling force linearly increaseswith time, while the particle is motionless att = 0s untilit reaches a maximum force of100 Nattimet = 4s. If the ground has staticand kinetic friction coefficients of u, = 0.6 andHU, = 0.4 respectively, determine the velocityof the A 1 0 - kg box is pulled along P , N a rough surface by a force P , as shown in the figure. The pulling force linearly increases with time, while the particle is motionless at t = 0 s untilit reaches a maximum force of 1 0 0 Nattimet = 4 s . If the ground has static and kinetic friction coefficients of u , = 0 . 6 and HU , = 0 . 4 respectively, determine the velocity of the particle att = 4 s .arrow_forwardCalculate the speed of the driven member with the following conditions: Diameter of the motor pulley: 4 in Diameter of the driven pulley: 12 in Speed of the motor pulley: 1800 rpmarrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





