Chapter 1.16, Problem 1MP

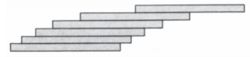
1. Show that it is possible to stack a pile of identical books so that the top book is as far as you like to the right of the bottom book. Start at the top and each time place the pile already completed on top of another book so that the pile is just at the point of tipping. (In practice, of course, you can’t let them overhang quite this much without having the stack topple. Try it with a deck of cards.) Find the distance from the right-hand end of each book to the right-hand end of the one beneath it. To find a general formula for this distance, consider the three forces acting on book n, and write the equation for the torque about its right-hand end. Show that the sum of these setbacks is a divergent series (proportional to the harmonic series). [See "Leaning Tower of The Physical Reviews," Am. J. Phys. 27, 121-122 (1959).]



2. By computer, find the sum of N terms of the harmonic series with N = 25, 100, 200, 1000, 10⁶, 10¹⁰⁰.
3. From the diagram in (a), you can that with 5 books (count down from the top) the top book is completely to the right of the bottom book, that is, the overhang is slightly over one book. Use your series in (a) to verify this. Then using parts (a) and (b) and a computer as needed, find the number of books needed for an overhang of 2 books, 3 books, 10 books, 100 books.