
Concept explainers
a.
ToEvaluate:The slope of the graph of
a.
Answer to Problem 49E
The slope of the graph of
Explanation of Solution
Given:
The function
Concept Used:
The slope
Calculation:
Given the function
The slope
At
Therefore, slope of the graph of
Conclusion:
Theslope of the graph of
b.
ToEvaluate: The equation of the tangent line to the graph of
b.
Answer to Problem 49E
The equation of the tangent line at the point
Explanation of Solution
Given:
The function
And from part a.) slope of the graph of
Concept Used:
The equation of the tangent line to the graph of a function
Calculation:
From part a.) the slope of the graph of
The equation of the tangent line at the point
Therefore, the equation of the tangent line at the point
Conclusion:
The equation of the tangent line at the point
c.
ToGraph:The function
c.
Answer to Problem 49E
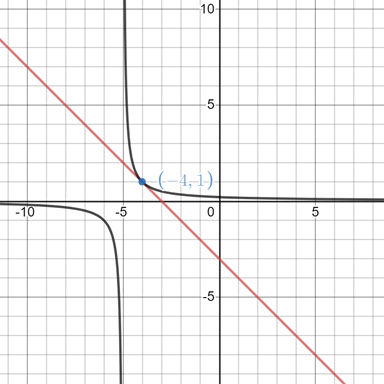
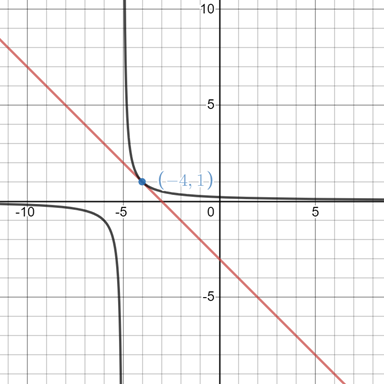
The graph of the function
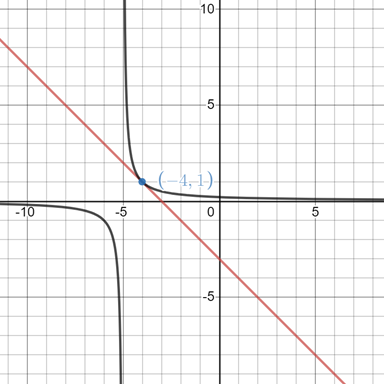
Explanation of Solution
Given:
The function
And from part b.) the equation of tangent line is
Concept Used:
The graph of a function is the smooth curve, which is the collection of all the points that satisfy the particular function.
Calculation:
For the function
And the tangent line
Plotting both of them on the same graph using a graphing utility, we have
Conclusion:
The graph of the function
Chapter 11 Solutions
Precalculus with Limits: A Graphing Approach
- Evaluate the following integrals, showing all your workingarrow_forwardConsider the function f(x) = 2x³-4x2-x+1. (a) Without doing a sketch, show that the cubic equation has at least one solution on the interval [0,1]. Use a theorem discussed in lectures, or see Section 1.8 of Calculus (7th ed) by Stewart. Ensure that the conditions of the theorem are satisfied (include this in your solution) (b) Now, by sketching the cubic (by hand or by computer), you should see that there is, in fact, exactly one zero in the interval [0,1]. Use Newton's method to find this zero accurate to 3 decimal places. You should include a sketch of the cubic, Newton's iteration formula, and the list of iterates. [Use a computer if possible, e.g., a spreadsheet or MatLab.]arrow_forwardEvaluate the following integrals, showing all your workingarrow_forward
- Differentiate the following functionarrow_forwardDifferentiate the following functionarrow_forwardA box with a square base and open top must have a volume of 13,500 cm³. Find the dimensions that minimise the amount of material used. Ensure you show your working to demonstrate that it is a minimum.arrow_forward
- Consider the equation, f(x) = x*. (a) Using the trapezoidal method with 3 columns, estimate the value of the integral f² f(x)dx. (b) Using the trapezoidal method with 10 columns, estimate the value of the integral f² f(x)dx. You many need software to help you do this (e.g. MATLAB, Excel, Google sheets). (c) Use software to accurately calculate the integral (e.g. Wolfram alpha, Matlab). Using this answer, comment on the answers you found in parts a) and b).arrow_forwardUsing the first-principles definition of differentiation, find the derivative of f(x) = = 2x²arrow_forwardEvaluate the following integrals, showing all your workingarrow_forward
- Differentiate the following functionarrow_forwardQuestion 1. (10 points) A researcher is studying tumours in mice. The growth rate for the volume of the tumour V(t) in cm³ is given by dV = 1.45V(2 In(V+1)). dt (a) (4 pts) Find all the equilibria and determine their stability using the stability condition. (b) (2 pts) Draw the phase plot f(V) versus V where f(V) = V'. You may find it helpful to use Desmos or Wolfram Alpha to plot the graph of f(V) versus V (both are free to use online), or you can plot it by hand if you like. On the plot identify each equilibrium as stable or unstable. (c) (4 pts) Draw direction arrows for the case where the tumour starts at size 3cm³ and for the case where the tumour starts at size 9cm³. Explain in biological terms what happens to the size of each of these tumours at time progresses.arrow_forwardFor the system consisting of the two planes:plane 1: -x + y + z = 0plane 2: 3x + y + 3z = 0a) Are the planes parallel and/or coincident? Justify your answer. What does this tell you about the solution to the system?b) Solve the system (if possible). Show a complete solution. If there is a line of intersection express it in parametric form.arrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





