8th Edition

ISBN: 9781265370749

Author: ROSEN

Publisher: MCG

See similar textbooks

Videos

Textbook Question

Chapter 11.2, Problem 14E

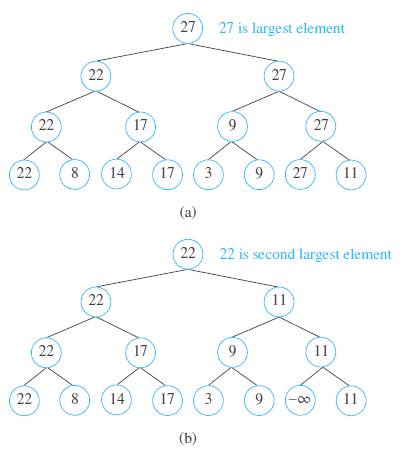
The tournament sort is a sorting algorithm that works by building an ordered binary tree. We represent the elements to be sorted by vertices that sill become the leaves. We build up the tree one level at a time we would construct the tree representing the winners of matches in a tournament Working left to right, we compare pairs of consecutive elements, adding a parent vertex labeled with the larger of the two elements under comparison. We make similar comparisons between labels of vertices at each level until we reach the root of the tree that is labeled with the largest element. The tree constructed by the tournament sort of , 8.14,17,3,9,27,11 is ilinstrated in part(a)ef the figure. Once the argestelementhbeendetermined. The leaf with this labelisrelabeled by -s,which is definedtobelessthanevery element The labels of all vertices on the path from this vertex up to the root of the tree are recalculated, as shown in part (b) of the figure.

This produces the second largest element This process continues until the entire list has been sorted.

Chapter 11.2, Problem 14E, The tournament sort is a sorting algorithm that works by building an ordered binary tree. We

14. Use the tournament sort to sort the list 17, 4, 1, 5, 13, 10, 14, 6.

Expert Solution & Answer

Want to see the full answer?

Check out a sample textbook solution

See solution

Chapter 11.2, Problem 13E

Chapter 11.2, Problem 15E

Students have asked these similar questions

For the position function s(t) = - 16t² + 105t, complete the following table with the appropriate average velocities. Then make a conjecture about the value of the instantaneous velocity at t = 1. Time Interval Average Velocity [1,2] Complete the following table. Time Interval Average Velocity [1, 1.5] [1, 1.1] [1, 1.01] [1, 1.001] [1,2] [1, 1.5] [1, 1.1] [1, 1.01] [1, 1.001] ப (Type exact answers. Type integers or decimals.) The value of the instantaneous velocity at t = 1 is (Round to the nearest integer as needed.)

Find the following limit or state that it does not exist. Assume b is a fixed real number. (x-b) 40 - 3x + 3b lim x-b x-b ... Select the correct choice below and, if necessary, fill in the answer box to complete your choice. (x-b) 40 -3x+3b A. lim x-b x-b B. The limit does not exist. (Type an exact answer.)

x4 -289 Consider the function f(x) = 2 X-17 Complete parts a and b below. a. Analyze lim f(x) and lim f(x), and then identify the horizontal asymptotes. x+x X--∞ lim 4 X-289 2 X∞ X-17 X - 289 lim = 2 ... X∞ X - 17 Identify the horizontal asymptotes. Select the correct choice and, if necessary, fill in the answer box(es) to complete your choice. A. The function has a horizontal asymptote at y = B. The function has two horizontal asymptotes. The top asymptote is y = and the bottom asymptote is y = ☐ . C. The function has no horizontal asymptotes. b. Find the vertical asymptotes. For each vertical asymptote x = a, evaluate lim f(x) and lim f(x). Select the correct choice and, if necessary, fill in the answer boxes to complete your choice. e

Chapter 11 Solutions

DISCRETE MATH CONNECT ACCESS

Ch. 11.1 - Prob. 1E Ch. 11.1 - Vhich of these graphs are trees?Ch. 11.1 - Prob. 3E Ch. 11.1 - Prob. 4E Ch. 11.1 - Prob. 5E Ch. 11.1 - Prob. 6E Ch. 11.1 - Prob. 7E Ch. 11.1 - Prob. 8E Ch. 11.1 - Prob. 9E Ch. 11.1 - Prob. 10E

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.

Solution Summary: The author explains that the first two steps are shown in the . The parent of a pair is then the larger element of the two leaves.

Videos

Want to see the full answer?

Chapter 11 Solutions