Chapter 11.1, Problem 15SSC

(a)

To determine

To explain: the consequences in terms of work and energy.

To draw: a bar graph for this situation.

Explanation of Solution

Introduction:

Work done on an object is equal to the product of the force applied on the object $F$ and the displacement of the object $s$ in the direction of force.

The expression for the work done is given by

  $W=F.s$  ......(1)

The person uses an air hose to apply force on the puck and thus the force displaces the puck to a certain distance. So, from the definition of work done, work is said to be done on the puck. If the person applied a force $F$ on the puck, it is displaced to a distance of $d$ m, then the work done on the puck is

  $W=F.d$  ......(2)

Work done on object is used to change the energy of the object. Initially, work is done on the puck to move it a certain distance and a because of the work done on the puck, it undergoes motion. Therefore, the puck possesses kinetic energy in the final state.

Final kinetic energy is $K{E}_f$ .

Initial kinetic energy is $K{E}_i$ .

Equation for work done on the puck is

  $W=K{E}_f-K{E}_i$

  $W=\frac{1}{2}m{v}_f^2-\frac{1}{2}m{v}_i^2$  ......(3)

Since the puck is initially at rest, $v_i=0\text{m/s}$ .

Equation (3) becomes,

  $W=\frac{1}{2}m{v}_f^2$  ......(4)

The following is the energy bar graph of the puck on the frictional air table. Initial kinetic energy of the puck is zero. The work done on the puck is equal to final kinetic energy.

  

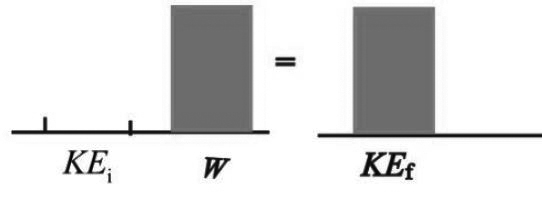
(b)

To determine

To describe: The manner kinetic energy and work done should differ from those in the first situation.

Explanation of Solution

Introduction:

Work done on an object is equal to the product of the force applied on the object $F$ and the displacement of the object $s$ in the direction of force.

If the mass of the puck is reduced to half $\frac{m}{2}$ and the same amount of force $F$ is applied on the puck, then the puck will undergo same displacement as that of displacement of the puck of mass $m$ because both masses move equal distances on a frictionless surface. Thus, the work done on the puck of mass $\frac{m}{2}$ , $W^{\prime }$ is equal to the work done on the puck of mass $m$ .

The expression the work done $W^{\prime }$ is

  $W^{\prime }=\frac{1}{2}\left(\frac{m}{2}\right)v^2{}_f$

Work done on the puck of mass $\frac{m}{2}$ is equal to the change in the kinetic energy of the puck and it is also equal to the work done on the puck of mass $m$ . So, the change in the kinetic energy of the puck of mass $\frac{m}{2}$ also equal to the change in the kinetic energy of the puck of mass $m$ .

Since the work done on the puck of mass $m$ and $\frac{m}{2}$ is equal, one can write,

  $\begin{array}{l}W=W^{\prime }\\ \frac{1}{2}m{v}_f^2=\frac{1}{2}\left(\frac{m}{2}\right){v^{\prime }}_f^2\\ {v^{\prime }}_f=\sqrt{2}{v}_f\\ {v^{\prime }}_f=1.41v_f\end{array}$

Conclusion:

Hence, the smaller mass puck moves with a velocity that is 1.41 times that of the velocity of the larger puck.

(c)

To determine

To describe: The situation in part a, and b in terms of impulse and momentum.

Explanation of Solution

Introduction:

Work done on an object is equal to the product of the force applied on the object $F$ and the displacement of the object $s$ in the direction of force.

Momentum of an object is the product of its mass $m$ and its velocity $v$ .

  $p=mv$  ......(1)

Impulse is equal to the change in momentum,

  $J=dp$  ......(2)

Use equation (1) in equation (2)

  $J=m{v}_f-m{v}_i$  ......(3)

The momentum of the puck of mass $m$ is

  $p=m{v}_f$  ......(4)

The momentum of the puck of mass $\frac{m}{2}$ is

  $p^{\prime }=\left(\frac{m}{2}\right){v^{\prime }}_f$  ......(5)

Divide equation (4) by equation (5)

  $\frac{p}{p^{\prime }}=\frac{m{v}_f}{\left(\frac{m}{2}\right){v^{\prime }}_f}s$

  $\frac{p}{p^{\prime }}=\frac{2v_f}{{v^{\prime }}_f}$  ......(6)

Substitute the value of ${v^{\prime }}_f$ in equation (6)

  $\begin{array}{l}{p}^{\prime }=\frac{2\times 1.41v_f}{{v^{\prime }}_f}p\\ p^{\prime }=0.707p\end{array}$

From the above equation, it is clear that the pucks of mass $m$ and mass $\frac{m}{2}$ will not have same momentum and the momentum of the pucks of mass $\frac{m}{2}$ is small that that of the pucks of mass $m$ .

The impulse on the puck of mass $m$ is

  $J=m{v}_f$  ......(7)

The impulse on the puck of mass $\frac{m}{2}$ is

  $J^{\prime }=\left(\frac{m}{2}\right){v^{\prime }}_f$  ......(8)

Divide equation (7) by (8),

  $\frac{J}{J^{\prime }}=\frac{m{v}_f}{\left(\frac{m}{2}\right){v^{\prime }}_f}$

  $\frac{J}{J^{\prime }}=\frac{2v_f}{{v^{\prime }}_f}$  ......(9)

Substitute the value of ${v^{\prime }}_f=1.41v_f$ in equation (9)

  $\begin{array}{l}{J}^{\prime }=\frac{1.41v_f}{2v_f}J\\ J^{\prime }=0.707J\end{array}$

From the equation, it is clear that the pucks of mass $m$ and mass $\frac{m}{2}$ will not have the same mass impulse and the impulse of the pucks of mass $\frac{m}{2}$ is small that of the pucks of mass $m$ .

Conclusion:

Hence, it is described the situation of part a and b in terms of impulse and momentum.