
(a)
To find: The graph of
(a)
Answer to Problem 64E
The graph is shown:
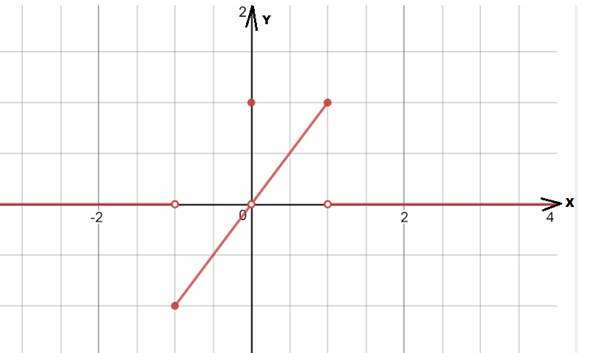
Explanation of Solution
Given information: The function is:
Graph:
The graph of the given function is shown below:
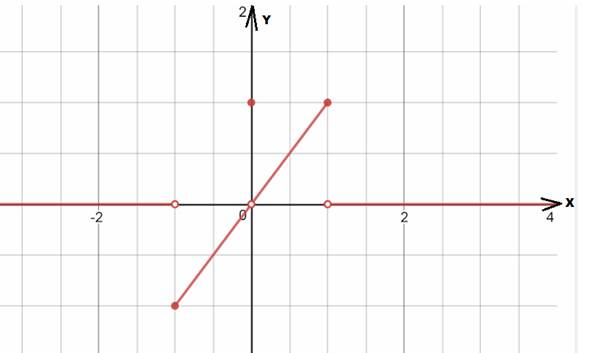
(b)
To find: The points of c in the domain of
(b)
Answer to Problem 64E
Explanation of Solution
Given information: The function is:
Calculation:
The domain of the function is
The limit does not exists at
Since the left and right hand limits at those points are not equal.
Therefore the required the limits exists for all
(c)
To find: The points that c does only the left hand limits exits.
(c)
Answer to Problem 64E
None.
Explanation of Solution
Given information: The function is:
Calculation:
The limit is evident from 64b at all places other than
However, whether or not they are equal, there are left- and right-hand limitations at certain locations. Thus, there are points where only the left-hand limit is present, such as at,0no points.
(d)
To find: The points that c does only the right hand limits exits.
(d)
Answer to Problem 64E
None.
Explanation of Solution
Given information: The function is:
Calculation:
The limit is evident from 64b at all places other than
However, whether or not they are equal, there are left- and right-hand limitations at certain locations. There are therefore "no points" where the right-hand limit is the only one that exists.
Chapter 1 Solutions
AP CALCULUS TEST PREP-WORKBOOK
- EXAMPLE 3 Find S X √√2-2x2 dx. SOLUTION Let u = 2 - 2x². Then du = Χ dx = 2- 2x² = 信 du dx, so x dx = du and u-1/2 du (2√u) + C + C (in terms of x).arrow_forwardLet g(z) = z-i z+i' (a) Evaluate g(i) and g(1). (b) Evaluate the limits lim g(z), and lim g(z). 2-12 (c) Find the image of the real axis under g. (d) Find the image of the upper half plane {z: Iz > 0} under the function g.arrow_forwardk (i) Evaluate k=7 k=0 [Hint: geometric series + De Moivre] (ii) Find an upper bound for the expression 1 +2x+2 where z lies on the circle || z|| = R with R > 10. [Hint: Use Cauchy-Schwarz]arrow_forward
- Hint: You may use the following derivative rules: ddxsin(x)=cos(x) ddxcos(x)=−sin(x) ddxln(x)=1x Find the equation of the tangent line to the curve y=4sinx at the point (π6,2).The equation of this tangent line isarrow_forwardQuestion Find the following limit. Select the correct answer below: 1 2 0 4 5x lim sin (2x)+tan 2 x→arrow_forward12. [0/1 Points] DETAILS MY NOTES SESSCALCET2 5.5.022. Evaluate the indefinite integral. (Use C for the constant of integration.) sin(In 33x) dxarrow_forward
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning





