
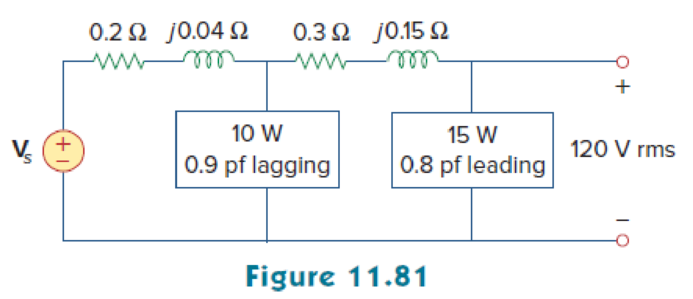
For the circuit in Fig. 11.81, find Vs.
Find the voltage
Answer to Problem 62P
The voltage
Explanation of Solution
Given data:
Refer to Figure 11.81 in the textbook.
The voltage
For load A,
The real power
The power factor
For load B,
The real power
The power factor
Formula used:
Write the expression to find the complex power.
Here,
Write the expression to find the power factor
Here,
Write the expression to find the real power.
Write the expression to find the reactive power.
Write the expression to find the output voltage.
Calculation:
The given Figure 11.81 is redrawn as shown in Figure 1.
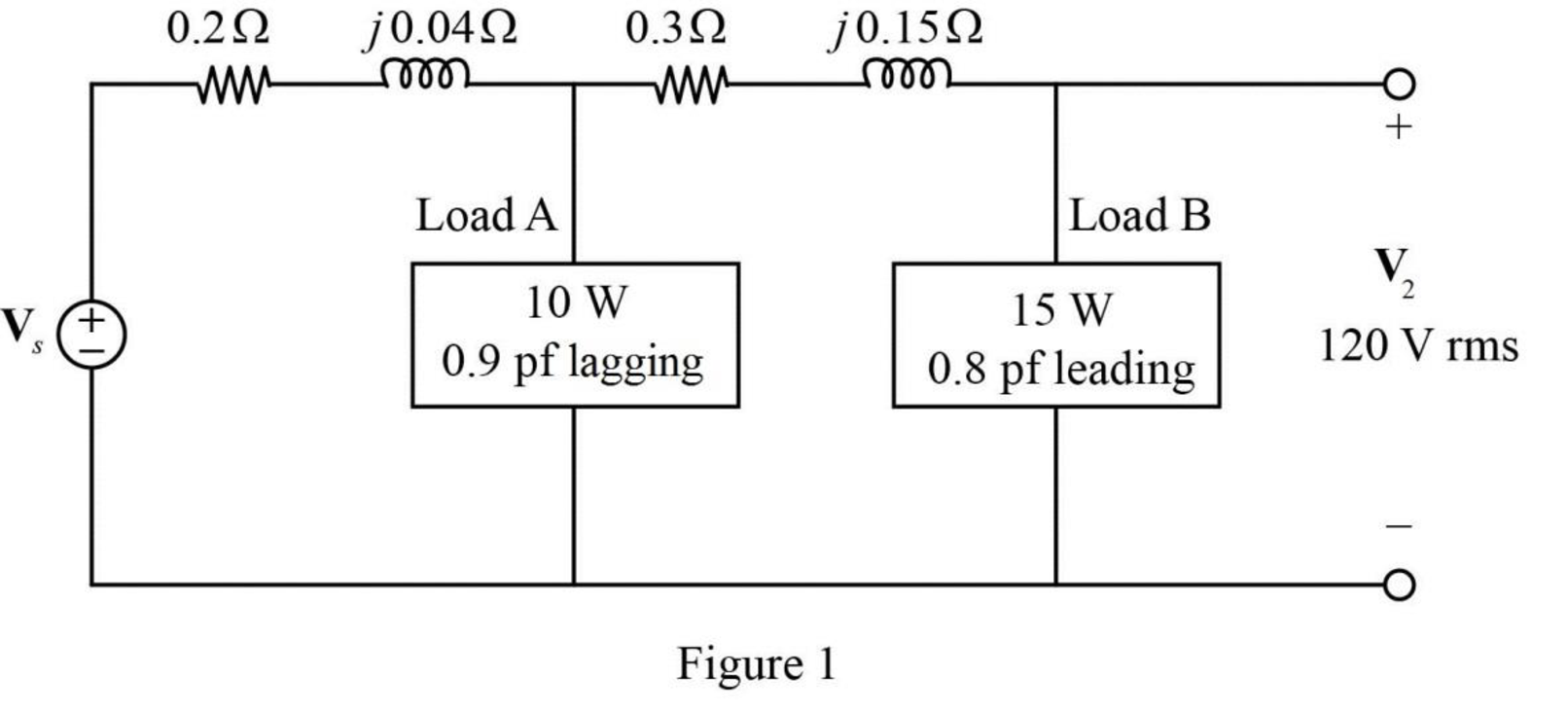
For load A:
Substitute
Substitute
Rearrange the equation as follows,
Substitute
Substitute
For load B:
Substitute
Substitute
Rearrange the equation as follows,
Substitute
Substitute
As the power factor is leading, the load is capacitive. Therefore, the equation becomes,
The modified Figure is shown in Figure 2.
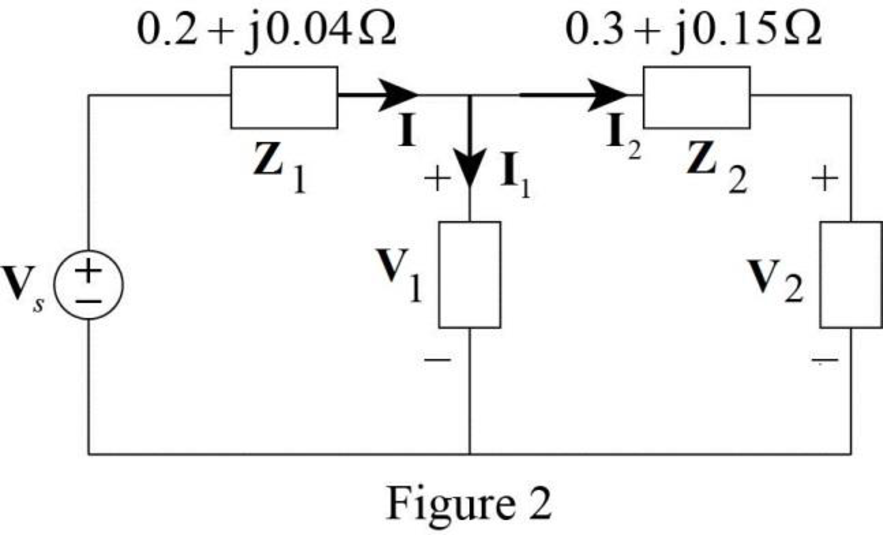
Substitute
The voltage
Substitute
Substitute
Convert the equation from polar to rectangular form.
The current
Substitute
The voltage supplied by the source is,
Substitute
Convert the equation from rectangular to polar form.
Conclusion:
Thus, the voltage
Want to see more full solutions like this?
Chapter 11 Solutions
EBK FUNDAMENTALS OF ELECTRIC CIRCUITS
- The project conditions are:The project functionality will be provided as per the project description suppliedbelow.You must present/demonstrate the project as a group, at the given time,andwithin a given time limit ( 20 mins ).A soft copy of all project documents is required before you The program functionality should be as follows:• Upon entering the “run” mode all counters/timers must be reset (use the first scan bit).• When students scan RFID cards, the opening motor automatically opens the door and closing motor closes it after a 5 second wait.• The current number of students should be counted by incrementing/decrementing as students enter or leave the classroom. • The number of students entering the classroom is counted using a reflective sensor, while the number leaving is counted using a fiber optic sensor. The count should be displayed in the decimal tag "Total no of students”.• The maximum number of students in the classroom is 20, and when the classroom is occupied by the…arrow_forwardSolve this problem and show all of the workarrow_forward1. The circuit below has R1 =R2 R3 = 10 kohms and R4 = 2.5 kohms. For V1 = 5 V and V2 = 4.2 V, determine: (a) Vx (b) lx (c) VR (d) Va (e) Vb (1) Vo ww Rarrow_forward
- I need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forwardI need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forwardI need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forward
- I need help with this problem and an step by step explanation of the solution from the image described below. (Introduction to Signals and Systems)arrow_forward2) Design the circuit shown in Figure 2 to provide bias current of IQ2= 150 uA. Assume circuit parameters of IREF2 = 250 UA, V+ = 3 V, and V = -3 V. The transistor parameters are VTP = -0.6 V, λ = 0, K'p= 40 uA/V², W/Lc = 15 and W/LA = 25. V+ Mc + VSGC VSGB + MB VSGA + + MA VSDA IREF2 V- Figure 2 ww RD=8kQarrow_forward٣/١ a い يكا +91- PU + 96852 A. For the RL-circuit with i(0)=0, Find the current i(t) using LT R=2 V(t)=sin3t L=1H B. Find Invers Laplace Transform for Z(s) = = 220125 750 x2.01 4s2 +2s+3 s2-3s+2arrow_forward
 Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
Delmar's Standard Textbook Of ElectricityElectrical EngineeringISBN:9781337900348Author:Stephen L. HermanPublisher:Cengage Learning
