
In this exercise we will develop an algorithm to find the strong components of a directed graph G = (V, E).
Recall that a vertex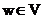 is reachable from a vertex
is reachable from a vertex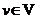 if there is a directed path from u to w.
if there is a directed path from u to w.
a) Explain how to use breadth-first search in the directed graph G to find all the vertices reachable from a
vertex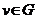
b) Explain how to use breadth-first search in Gcov to find all the vertices from which a vertex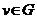 is
is
reachable. (Recall that Gcov is the directed graph obtained from G by reversing the direction of all its
edges.)
e) Explain how to use parts (a) and (b) to construct an algorithm that finds the strong components of a
directed graph G, and explain why your algorithm is correct.
Want to see the full answer?
Check out a sample textbook solution
Chapter 11 Solutions
Discrete Mathematics and Its Applications ( 8th International Edition ) ISBN:9781260091991
- I have a graph with 2021 vertices. It is not a tree but there exists some vertex whose removal makes it a tree. What is the maximum possible number of edges in the original graph?arrow_forwardCompute the betweenness centrality of all four verticesarrow_forwardShow that any graph with two or more nodes and no self-loops contains two nodes that have equal degrees.arrow_forward
- Explain thoroughly!! And please complete all 4 partsarrow_forwardDraw a directed graph with as few edges as possible that is strongly-connected, has 8 vertices of which one has in-degree 3, two have out-degree 3, and the rest have smaller in- and out-degrees. Prove that your graph has the minimum number of edges. (Create the drawing in any drawing editor and include it as an image in your answer.)arrow_forwardShow that the maximum number of edges in a graph with n-vertices is *C2 (d)arrow_forward
- Please solve 4barrow_forwardProve that a graph with at least three vertices is connected if and only if atleast two of the vertex-deleted subgraphs are connected.arrow_forwarddetermine the number of vertices and edgesand find the in-degree and out-degree of each vertex for thegiven directed multigraph.arrow_forward
- A school consists of 6 separate buildings, represented by the vertices in the graph. There are paths between some of the buildings as shown. The graph also shows the length in feet of each path. School administrators want to cover some of these paths with roofs so that students will be able to walk between buildings without getting wet when it rains. To minimize cost, they must select paths to be covered such that the total length to be covered is as small as possible. Use Kruskal's algorithm to determine which paths to cover. Also determine the total length of pathways to be covered. OA. Click here to view figure c. OC. Click here to view figure b. A The total length of pathways to be covered is (Type a whole number.) 45 B Find a minimum spanning tree. Choose the correct answer below. 51 34 19 39 25 E 31 29 30 25 F41 (... D 35 O B. Click here to view figure d. O D. Click here to view figure a.arrow_forwardCalculate the maximum edge count for 4 loop G graph by drawing figures.arrow_forwarddraw all nonisomorphic simple graphs with four vertices and no more than two edgesarrow_forward
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
