Chapter 11, Problem 1RQ

To determine

(a)

To define:

A tree.

Explanation of Solution

Definition: A tree is a connected undirected graph with no simple circuits. Because a tree cannot have a simple circuit, a tree cannot contain multiple edges or loops. Therefore any tree must be a simple graph.

An undirected graph is a tree if and only if there is a unique simple path between any two of its vertices.

Example:

To determine

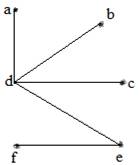
(b)

To define:

A forest.

Explanation of Solution

Definition: A forest is an undirected graph, all of whose connected components are trees.

i.e. the graph consists of a disjoint union of trees.

A forest is a disjoint union of trees, or equivalently anacyclic graph that is not necessarily connected.

Example:

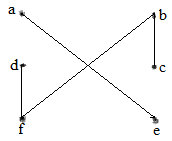
An empty graph, a single tree and the discrete graph on a set of vertices are examples of forest tree.