
Concept explainers
(a)
The
(a)
Answer to Problem 41P
Yes, the bullet has angular momentum about the door fixing axis.
Explanation of Solution
Write the expression for angular momentum for an object as.
Here,
Force acting on the door-bullet system as shown below.
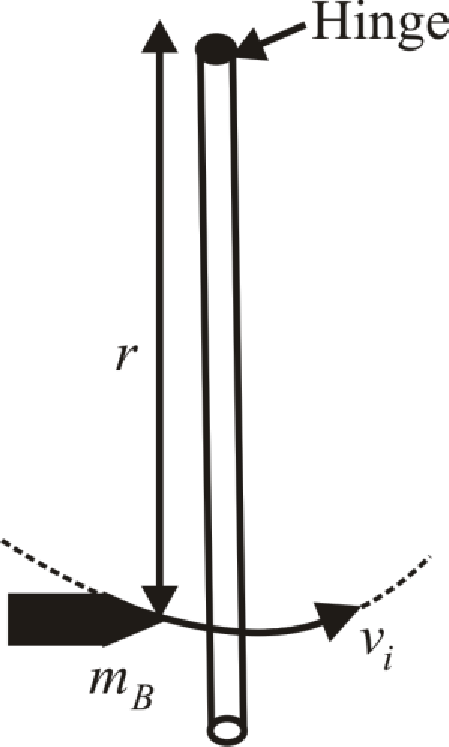
Conclusion:
Yes, the bullet has angular momentum about the door. The value of angular momentum for bullet will be the product of the moment of inertia of bullet and the angular speed of the bullets.
Thus, yes the bullet has angular momentum about the door fixing axis.
(b)
The angular momentum for bullet relative to the door’s axis of rotation.
(b)
Answer to Problem 41P
The angular momentum for bullet relative to the door’s axis of rotation is
Explanation of Solution
Conclusion:
Substitute
Thus, the angular momentum for bullet relative to the door’s axis of rotation is
(c)
The mechanical energy of the bullet– door system during this collision.
(c)
Answer to Problem 41P
The mechanical energy of the bullet-door system during this collision will not remain constant.
Explanation of Solution
Conclusion:
The collision of bullet and door is an inelastic collision; therefore, the mechanical energy of the bullet door system will not remain constant during a collision. In an inelastic collision, there is high friction between bullet and door so the amount of mechanical energy or kinetic energy of the bullet converts into internal energy of the bullet door system.
Thus, the mechanical energy of the bullet-door system during this collision will not remain constant.
(d)
The angular speed at which the door swing open immediately after the collision.
(d)
Answer to Problem 41P
The angular speed at which the door swing open immediately after the collision is
Explanation of Solution
Write the expression for moment of inertia of a bullet as.
Here,
Write the expression for moment of inertia for a stick or thin rod when it pivoted at another end as.
Here,
Write the expression for total moment of inertia which is the sum of MOI’s of door and bullet as.
Write the expression for total angular momentum as.
Here,
For conservation of angular momentum, equate the angular momentum of the bullet to the final angular momentum of door and bullet mass system as.
Conclusion:
Substitute
Simplify the above expression for
Thus, the angular speed at which the door swing open immediately after the collision is
(e)
The kinetic energy of the door-bullet system immediately after impact.
(e)
Answer to Problem 41P
The kinetic energy of the door-bullet system immediately after impact
Explanation of Solution
Write the expression for rotational kinetic energy as.
Here,
Write the expression for kinetic energy for the bullet as.
Here,
Substitute
Conclusion:
Substitute
Substitute
Thus, the kinetic energy of the door-bullet system immediately after impact
Want to see more full solutions like this?
Chapter 11 Solutions
Bundle: Physics for Scientists and Engineers with Modern Physics, Loose-leaf Version, 9th + WebAssign Printed Access Card, Multi-Term
- 3.77 is not the correct answer!arrow_forwardA I squar frame has sides that measure 2.45m when it is at rest. What is the area of the frame when it moves parellel to one of its diagonal with a m² speed of 0.86.c as indicated in the figure? >V.arrow_forwardAn astronent travels to a distant star with a speed of 0.44C relative to Earth. From the austronaut's point of view, the star is 420 ly from Earth. On the return trip, the astronent travels speed of 0.76c relative to Earth. What is the distance covered on the return trip, as measured by the astronant? your answer in light-years. with a Give ly.arrow_forward
- star by spaceship Sixus is about 9.00 ly from Earth. To preach the star in 15.04 (ship time), how fast must you travel? C.arrow_forwardIf light-bulb A is unscrewed, how will the brightness of bulbs B and C change, if at all? How does the current drawn by from the battery change?arrow_forwardCan someone help mearrow_forward
- Can someone help me with this thank youarrow_forward(a) For a spherical capacitor with inner radius a and outer radius b, we have the following for the capacitance. ab C = k₂(b- a) 0.0695 m 0.145 m (8.99 × 10º N · m²/c²)( [0.145 m- 0.0695 m × 10-11 F = PF IIarrow_forwardA pendulum bob A (0.5 kg) is given an initialspeed of vA = 4 m/s when the chord ishorizontal. It then hits a stationary block B (1kg) which then slides to a maximum distanced before it stops. Determine the value of d.The coefficient of static friction between theblock and the plane is μk = 0.2. The coefficientof restitution between A and B is e = 0.8.Ans: d=1.0034 marrow_forward
- Figure 29-43 Problem 12. ••13 In Fig. 29-44, point P₁ is at distance R = 13.1 cm on the perpendicular bisector of a straight wire of length L = 18.0 cm carrying current i = 58.2 mA. (Note that the wire is not long.) What is the magnitude of the magnetic field at P₁ due to i? P2° R R Larrow_forwardCheckpoint 1 The figure shows the current i in a single-loop circuit with a battery B and a resistance R (and wires of neg- ligible resistance). (a) Should the emf arrow at B be drawn pointing leftward or rightward? At points a, B C R b, and c, rank (b) the magnitude of the current, (c) the electric potential, and (d) the electric potential energy of the charge carriers, greatest first.arrow_forwardPls help ASAParrow_forward
 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





