Chapter 1.1, Problem 20E

While it is difficult to imagine a time before cell phones, such a time did exist. The table below gives the number (in millions) of cell phone subscriptions in the United States from the U.S. census (see www.census.gov).
  
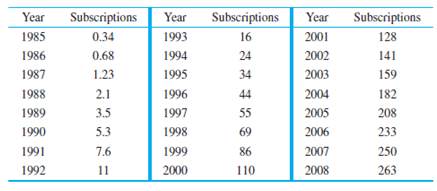
Let s(t) be the number of cell phone subscriptions at times, measured in years since 1989. The relative growth rate of x(t) is its growth rate divided by the number of subscriptions. In other words, the relative growth rate is
   $\frac{1}{s\left(t\right)}\frac{ds}{dt}$
and it is often expressed as a percentage.
(a) Estimate the relative growth rate of s(t) att = 1. That is, estimate the relative rate for the year 1990. Express this growth rate as a percentage. [Hint: The best estimate involves the number of cell phones at 1989 and 1991.]
(b) In general, if a quantity grows exponentially, how does its relative growth rate change?
(c) Also estimate the relative growth rates of s(t) for the years 1991—2007.
(d) How long after 1989 was the number of subscriptions growing exponentially?
(e) In general, if a quantity grows according to a logistic model, how does its relative growth rate change?
(f) Using your results in part (c), calculate the carrying capacity for this model. [Hint: There is more than one way to do this calculation.]