Chapter 11, Problem 11.DE

Interpretation Introduction

Interpretation:

The $pH$ values of the reaction medium during titration of $0.0500MMalonicacid-0.100MNaOH$ system has to be calculated for the given volumes of $NaOH$.  A graph of $pH$ versus volume of $NaOH$ added has to be drawn.

Concept introduction:

Acid-base titration is titration between acid and base. It is also known as neutralization reaction.

There are primarily four types of acid-base titrations –

• Strong base vs strong acid
• Strong base vs weak acid
• Weak base vs strong acid
• Weak base vs weak acid

The term $pH$ refers to concentration of $H^{+}$ion in a solution.

Answer to Problem 11.DE

The $pH$ values of the reaction medium during titration of $0.0500MMalonicacid-0.100MNaOH$ system are calculated for the given volumes of $NaOH$ as,

S.No	Volume of $NaOH$, $V_b$ $(mL)$	$pH$
1.	$0.0$	$2.11$
2.	$8.0$	$2.52$
3.	$12.5$	$2.85$
4.	$19.3$	$3.38$
5.	$25.0$	$4.28$
6.	$37.5$	$5.70$
7.	$50.0$	$9.05$
8.	$56.3$	$11.77$

The graph of $pH$ versus volume of $NaOH$ is plotted as,

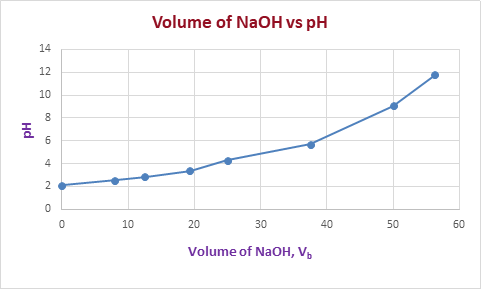
Explanation of Solution

Given that volume of base, $NaOH$ and it is denoted by $V_b.$ Given the strength ( $M_1$) and volume of Malonic acid $H{O}_{2}CC{H}_{2}C{O}_{2}H$ solution ( $V_1$) and strength of $KOH$( $M_2$), Since malonic acid is a diprotic acid two equivalence points do occur.

The reaction occurring in titration of malonic acid with $NaOH$ is represented as,

$\begin{array}{l}H{O}_{2}CHC{H}_{2}C{O}_{2}H+O{H}^{-}\stackrel{}{\to }\stackrel{-}{O_2}CHC{H}_{2}C{O}_{2}H+H_{2}O\\ \stackrel{-}{O_2}CHC{H}_{2}C{O}_{2}H{\text{ + OH}}^{-}\stackrel{}{\to }\stackrel{-}{O_2}CHC{H}_{2}C{O}_2^{-}\end{array}$

The volume of $NaOH$ added to reach first equivalence point ( $V_1$)is calculated as,

$\begin{array}{l}{V}_1{M}_1={\text{ V}}_2{\text{M}}_2\\ 50.0\text{ mL}\times \text{ 0}\text{.0500 M}{\text{= V}}_2\times 0.100M\\ V_2=\frac{50\text{ mL}\times \text{ 0}\text{.0500 M}}{0.100M}\\ =\text{ 25}\text{.0 mL}\end{array}$

Thus at first equivalence point $50mL$ of acid is converted to $50mL$ of monobasic anion.  Upon continual addition of base another proton left in monobasic anion is abstracted and dibasic anion is formed.  Thus at second equivalence point, $50mL$ of monobasic anion is converted to $50mL$ of dibasic anion.

The volume of $NaOH$ added to reach second equivalence point ( $V_2$)is calculated as,

$\begin{array}{l}{V}_1{M}_1={\text{ V}}_2{\text{M}}_2\\ 50.0\text{ mL}\times \text{ 0}\text{.0500 M}{\text{= V}}_2\times 0.100M\\ V_2=\frac{50\text{ mL}\times \text{ 0}\text{.0500 M}}{0.100M}\\ =\text{ 25}\text{.0 mL}\end{array}$

Thus after the addition of $25.0mL$ of base we further need to add $25.0mL$ of base to reach the second equivalence point.  Hence totally $25.0mL+25.0mL=50.0mL$ of base is required to reach second equivalence point from the beginning of the titration.

Let $H_{2}M$ be malonic acid.  When volume of base added is $0.00mL$, that is in absence of base, the $pH$ depends upon the dissociation of malonic acid.  Since it is a weak acid it doesn’t dissociate completely into individual ions.  The acid has two Ka values – K₁ and K₂ since it is diprotic acid.

$H_{2}M\stackrel{}{\rightleftharpoons }{H}^{+}+H{M}^{-}$

$[H^{+}]=[H{M}^{-}]=x,[H_{2}M]=0.0500-x$ and $K_1{\text{ of H}}_2\text{M is 1}\text{.42}\times {\text{10}}^{-3}$

$K_a$ for the above reaction is,

$\begin{array}{l}{K}_a=\frac{x^2}{0.0500-x}\\ \text{1}\text{.42}\times {\text{10}}^{-3}=\frac{x^2}{0.0500-x}\end{array}$

Solving for ‘x’,

$x=7.75\times {10}^{-3}M=[H^{+}]$

$pH$ is determined as,

$\begin{array}{l}pH\text{= - }\log \left[H^{+}\right]\\ =\text{ -log}\left(7.75\times {10}^{-3}\right)\\ \text{= 2}\text{.11}\end{array}$

When volume of $NaOH$ added is $8.0mL$, the base begins to react with acid.  Upon reaction with base the acid forms conjugate base.  The titrating mixture then becomes buffer.  The concentration of conjugate base formed increases with addition of base at each step. Using Henderson-Hasselbalch equation $pH$ can be determined.

The titration reaction at this instant is,

$H_{2}M+O{H}^{-}\stackrel{}{\to }H{M}^{-}+H_{2}O$

Their respective concentration is,

$\begin{array}{l}{H}_{2}M{\text{ + OH}}^{-}\stackrel{}{\to }H{M}^{-}{\text{ + H}}_2\text{O}\\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\\ Initial:\text{ 25 mL 8 mL - -}\\ \text{Final: 25-8 mL - 8 mL -}\end{array}$

Substitute the values known to determine $pH$ ,

$\begin{array}{l}pH{\text{= pK}}_1\text{+ }\log \frac{[H{M}^{-}]}{[H_{2}M]}\\ =\text{ 2}\text{.847 +log}\left(\frac{8}{17}\right)\\ \text{= 2}\text{.52}\end{array}$

When volume of $NaOH$ added is $12.5mL$, the base begins to react with acid.  Upon reaction with base the acid forms conjugate base.  The titrating mixture then becomes buffer.  The concentration of conjugate base formed increases with addition of base at each step. Using Henderson-Hasselbalch equation $pH$ can be determined.

The titration reaction at this instant is,

$H_{2}M+O{H}^{-}\stackrel{}{\to }H{M}^{-}+H_{2}O$

Their respective concentration is,

$\begin{array}{l}{H}_{2}M{\text{ + OH}}^{-}\stackrel{}{\to }H{M}^{-}{\text{ + H}}_2\text{O}\\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\\ Initial:\text{ 25 mL 12}\text{.5 mL - -}\\ \text{Final: 25-12}\text{.5 mL - 12}\text{.5 mL -}\end{array}$

Substitute the values known to determine $pH$ ,

$\begin{array}{l}pH{\text{= pK}}_1\text{+ }\log \frac{[H{M}^{-}]}{[H_{2}M]}\\ =\text{ 2}\text{.847 +log}\left(\frac{12.5}{12.5}\right)\\ \text{= 2}\text{.85}\end{array}$

When volume of $NaOH$ added is $19.3mL$, the base begins to react with acid.  Upon reaction with base the acid forms conjugate base.  The titrating mixture then becomes buffer.  The concentration of conjugate base formed increases with addition of base at each step. Using Henderson-Hasselbalch equation $pH$ can be determined.

The titration reaction at this instant is,

$H_{2}M+O{H}^{-}\stackrel{}{\to }H{M}^{-}+H_{2}O$

Their respective concentration is,

$\begin{array}{l}{H}_{2}M{\text{ + OH}}^{-}\stackrel{}{\to }H{M}^{-}{\text{ + H}}_2\text{O}\\ \_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\_\\ Initial:\text{ 25 mL 19}\text{.3 mL - -}\\ \text{Final: 25-19}\text{.3 mL - 19}\text{.3 mL -}\end{array}$

Substitute the values known to determine $pH$ ,

$\begin{array}{l}pH{\text{= pK}}_1\text{+ }\log \frac{[H{M}^{-}]}{[H_{2}M]}\\ =\text{ 2}\text{.847 +log}\left(\frac{19.3}{5.7}\right)\\ \text{= 3}\text{.38}\end{array}$

When volume of $NaOH$ added is $25.0mL$, $25.0mL$ of the acid has been converted to its conjugate base, monobasic anion as the first equivalence point is reached.

formal concentration of malonic acid at this instant is,

$F\text{ = }\left(\frac{50mL}{50mL+25mL}\right)\times 0.0500M=0.0333M$

Hence $[H^{+}]$ is determined as,

$\begin{array}{l}[H^{+}]=\sqrt{\frac{K_1+K_{2}F+K_1{K}_w}{K_1+F}}\\ =\sqrt{\frac{\left(1.42\times {10}^{-3}\right)+\left(2.01\times {10}^{-6}\times 0.0333\right)+\left(1.42\times {10}^{-3}\times 1\times {10}^{-14}\right)}{\left(1.42\times {10}^{-3}\right)+0.0333}}\end{array}$

Solving the above equation,

$[H^{+}]=5.23\times {10}^{-5}M$

Substitute the values known to determine $pH$ ,

$\begin{array}{l}pH\text{= -}\log [H^{+}]\\ =\text{ -log}\left(5.23\times {10}^{-5}\right)\\ \text{= 4}\text{.28}\end{array}$

After reaching the first equivalence point, continual addition of base forms dibasic anion.

When volume of base added is $37.5mL$,

Volume of base is equivalent to, $V_b=\frac{3}{2}{V}_e$

Therefore,

$\begin{array}{l}pH{\text{= pK}}_2\text{+ }\log \frac{[H{M}^{-}]}{[H_{2}M]}\\ =\text{ 5}\text{.70 +log}\left(\frac{37.5}{37.5}\right)\\ \text{= 5}\text{.70}\end{array}$

When volume of base added is $50mL$, second equivalence point is reached as calculated previously.  All of the monobasic anion, HM^- is completely converted to dibasic anion, M^2-.  Hydrolysis of dibasic anion determines the $pH.$ The reaction is

$M^{2-}+H_{2}O\stackrel{}{\rightleftharpoons }H{M}^{-}+O{H}^{-}$

Formal concentration of malonic acid is,

$\left(\frac{50mL}{50mL+50mL}\right)\times 0.0500M=0.025M$

Then $\left[H{M}^{-}\right]=[O{H}^{-}]=x,\left[M^2{}^{-}\right]=0.025-x$

$K_b$ of malonic acid is,

$\begin{array}{l}{K}_b=\frac{K_w}{K_{a2}}\\ =\frac{{10}^{-14}}{2.01\times {10}^{-6}}\end{array}$

Also,

$\begin{array}{l}{K}_b=\frac{x^2}{0.0250-x}\\ \frac{{10}^{-14}}{2.01\times {10}^{-6}}=\frac{x^2}{0.0250-x}\end{array}$

Solving the above equation for ‘x’,

$x=[O{H}^{-}]=1.12\times {10}^{-5}M$

Substitute the values known to determine $pH$ ,

$\begin{array}{l}pH+pOH=\text{ 14}\\ pH=\text{ 14 - }pOH\\ \text{= 14-}\left(\text{-log [}O{H}^{-}\text{]}\right)\\ \text{= 14-}\left(\text{-log(}1.12\times {10}^{-5}\text{)}\right)\\ \text{= 14 - 4}\text{.95 = 9}\text{.05}\end{array}$

When volume of acid added is $56.3mL$, concentration of $[O{H}^{-}]$ by excess addition of sodium hydroxide determines the $pH.$

$\begin{array}{l}\left[O{H}^{-}\right]=\left(\frac{56.3-50\text{ mL}}{\text{106}\text{.3 mL}}\right)\times 0.100M\\ =5.93\times {10}^{-3}M\end{array}$

Substitute the values known to determine $pH$ ,

$\begin{array}{l}pH+pOH=\text{ 14}\\ pH=\text{ 14 - }pOH\\ \text{= 14-}\left(\text{-log [}O{H}^{-}\text{]}\right)\\ \text{= 14-}\left(\text{-log(}5.93\times {10}^{-3}\text{)}\right)\\ \text{= 14 - 2}\text{.23 = 11}\text{.77}\end{array}$

The graph of $pH$ versus volume of $NaOH$ is plotted as,

Conclusion

The $pH$ values of the reaction medium during titration of $0.0500MMalonicacid-0.100MNaOH$ system was calculated using relevant formula and the graph of $pH$ versus volume of $NaOH$ was drawn.