Mechanics of Materials
9th Edition
ISBN: 9780133254426
Author: Russell C. Hibbeler
Publisher: Prentice Hall
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 11, Problem 11.52RP
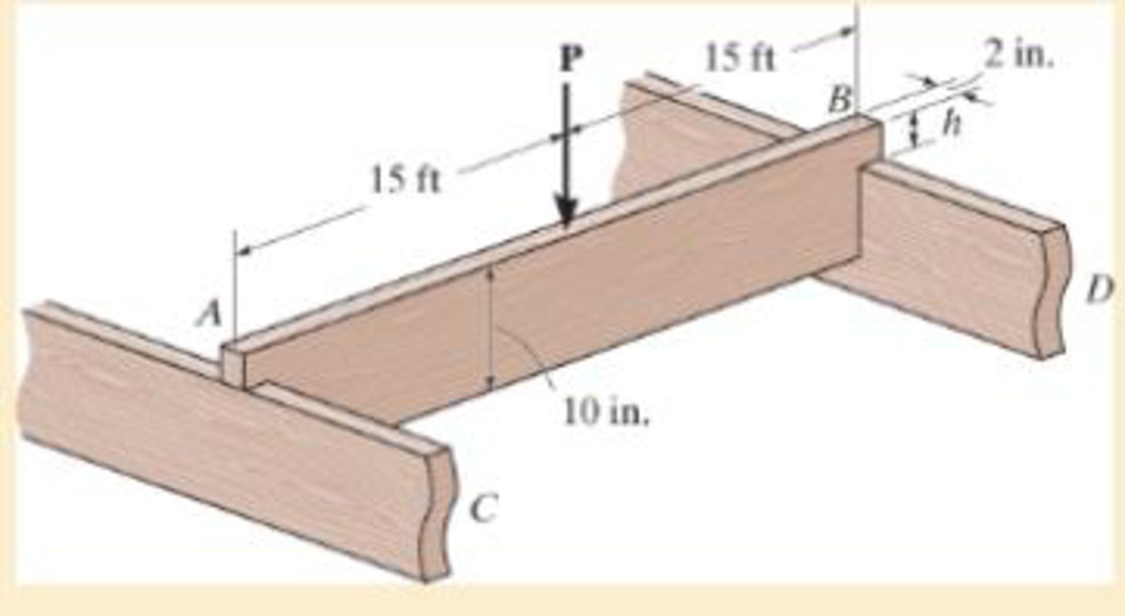
The simply supported joist is used in the construction of a floor for a building. In order to keep the floor low with respect to the sill beams C and D, the ends of the joists are notched as shown. If the allowable shear stress is τallow = 350 psi and the allowable bending stress is σallow = 1500 psi, determine the height h that will cause the beam to reach both allowable stresses at the same time. Also, what load P causes this to happen? Neglect the stress concentration at the notch.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
The simply supported joist is used in the construction of a floor for a building. In order to keep the floor low with respect to the sill beams C and D, the ends of the joist are notched as shown. If the allowable shear stress is tallow = 350 psi and the allowable bending stress is s allow = 1700 psi, determine the smallest height h so that the beam will support a load of P = 600 lb. Also, will the entire joist safely support the load? Neglect the stress concentration at the notch.
4
Find the second moment of area, the location of the neutral axis, and the distances from the neutral axis to the top and
bottom surfaces. Consider that the section is transmitting a positive bending moment about the z axis, Mz, where M₂ = 10
kip-in if the dimensions of the section are given in ips units, or M₂ = 1.13 kN·m if the dimensions are in Sl units. Determine
the resulting stresses at the top and bottom surfaces and at every abrupt change in the cross section.
From the figure,
с
- 12.5
B
A
y
I
50
100
75
12.5-
12.5
25
D
100
The area is determined to be 3750 mm²
The distances from the neutral axis to the top and bottom surfaces are determined to be 57.292
The second moment of area is determined to be 4.293
x 106 mm4.
mm and 42.708 ✪ mm.
Chapter 11 Solutions
Mechanics of Materials
Ch. 11.2 - Determine the minimum dimension a to the nearest...Ch. 11.2 - of the rod to safely support the load. The rod is...Ch. 11.2 - The wood has an allowable normal stress of allow =...Ch. 11.2 - of the beam's cross section to safely support the...Ch. 11.2 - Determine the minimum dimension b to the nearest...Ch. 11.2 - The beam is made of steel having an allowable...Ch. 11.2 - Determine its dimensions if it is to be...Ch. 11.2 - Determine the minimum width of the beam to the...Ch. 11.2 - if P=10 kip.Ch. 11.2 - If the allowable bending stress is allow = 22 ksi...
Ch. 11.2 - The allowable bending stress is allow = 24 ksi and...Ch. 11.2 - The allowable bending stress is allow = 22 ksi and...Ch. 11.2 - 11–7. Draw the shear and moment diagrams for the...Ch. 11.2 - *11–8. The simply supported beam is made of timber...Ch. 11.2 - The beam has an allowable normal stress of allow =...Ch. 11.2 - The beam has an allowable normal stress of allow...Ch. 11.2 - 11–11. The timber beam is to be loaded as shown....Ch. 11.2 - If each beam is to be designed to carry 90 lb/ft...Ch. 11.2 - 11–13. Select the lightest steel wide-flange beam...Ch. 11.2 - 11–14. Select the lightest-weight steel...Ch. 11.2 - Prob. 11.15PCh. 11.2 - The beam has an allowable normal stress of allow....Ch. 11.2 - Determine the maximum cable force P that can...Ch. 11.2 - to safely support the load. The wood has an...Ch. 11.2 - and the wood has an allowable normal stress of...Ch. 11.2 - Prob. 11.20PCh. 11.2 - Prob. 11.21PCh. 11.2 - Prob. 11.22PCh. 11.2 - 11–23. The beam is constructed from three boards...Ch. 11.2 - Prob. 11.24PCh. 11.2 - Prob. 11.25PCh. 11.2 - Select the lightest-weight wide-flange beam from...Ch. 11.2 - Prob. 11.27PCh. 11.2 - * 11–28. The joist AB used in housing construction...Ch. 11.2 - If the maximum bending stress is not to exceed...Ch. 11.2 - 11–30. The simply supported beam supports a load...Ch. 11.4 - Determine the variation in the width was a...Ch. 11.4 - Prob. 11.32PCh. 11.4 - Prob. 11.33PCh. 11.4 - The beam is made from a plate that has a constant...Ch. 11.4 - Determine the variation in the depth d of a...Ch. 11.4 - Determine the variation of the radius r of the...Ch. 11.4 - Prob. 11.37PCh. 11.4 - Determine the variation in the width b as a...Ch. 11.4 - The tubular shaft has an inner diameter of 15 mm....Ch. 11.4 - Prob. 11.40PCh. 11.4 - Prob. 11.41PCh. 11.4 - Prob. 11.42PCh. 11.4 - Prob. 11.43PCh. 11.4 - Prob. 11.44PCh. 11.4 - Prob. 11.45PCh. 11.4 - Prob. 11.46PCh. 11 - The cantilevered beam has a circular cross...Ch. 11 - Select the lightest-weight wide-flange overhanging...Ch. 11 - Prob. 11.49RPCh. 11 - Determine the shaft's diameter to the nearest...Ch. 11 - Select the lightest-weight wide-flange beam from...Ch. 11 - The simply supported joist is used in the...Ch. 11 - The simply supported joist is used in the...Ch. 11 - by 4-in. pieces of wood braced as shown. If the...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
List several uses of the arbor press.
Machine Tool Practices (10th Edition)
For the beam loading of Figure P334, draw the complete shearing force and bending moment diagrams, and determin...
Machine Elements in Mechanical Design (6th Edition) (What's New in Trades & Technology)
The moment of inertia Iy for the slender rod in terms of the rod’s total mass m .
Engineering Mechanics: Statics & Dynamics (14th Edition)
Comprehension Check 7-14
The power absorbed by a resistor can be given by P = I2R, where P is power in units of...
Thinking Like an Engineer: An Active Learning Approach (3rd Edition)
Locate the centroid of the area. Prob. 9-17
INTERNATIONAL EDITION---Engineering Mechanics: Statics, 14th edition (SI unit)
17–1C A high-speed aircraft is cruising in still air. How does the temperature of air at the nose of the aircra...
Thermodynamics: An Engineering Approach
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- Find the second moment of area, the location of the neutral axis, and the distances from the neutral axis to the top and bottom surfaces. Consider that the section is transmitting a positive bending moment about the z axis, Mz, where M₂ = 10 kip-in if the dimensions of the section are given in ips units, or M₂ = 1.13 kN·m if the dimensions are in Sl units. Determine the resulting stresses at the top and bottom surfaces and at every abrupt change in the cross section. From the figure Z 1 in 112 in y in → ← ¹ in 12 in D C B A ++ in The area is determined to be 2.0625 in². The distances from the neutral axis to the top and bottom surfaces are determined to be 0.858 x in and The second moment of area is determined to be 0.447 in 4. 1.017 xin.arrow_forwardDetermine the moment M that must be applied to the beam in order to create amaximum stress of 90 MPa. Also sketch the stress distribution acting over the cross section.arrow_forwardQuestion 1: A member having the dimensions shown is used to resist an internal bending moment of M kNm. Determine the maximum stress in the member if the moment is applied (a) about the z axis (as shown) (b) about the y axis. Sketch the stress distribution for each case. Take: M= 98 kNm mm A= 208 mm B= 158 mm B mm Solution: The moment of inertia of the cross-section about z and y axes are 1 AB³ 12 |(10-) m* 1 ВАЗ — 12 I, |(10) m* = For the bending about z axis, c = m Mc O pax MPа Iz For the bending about y axis, c = m Mc MPа Iy max z MPa KN=M Omax Y MPa. M KN-M MPa O max Z Omax Y MPaarrow_forward
- The axle of the freight train is subjected to loadings as shown below. The diameter of the axle is 137.5 mm. If it is supported by two journal bearings at C and D, determine the maximum bending Stress. Include a FBD, SFD and BMD using either the section or graphical method. Draw a cross-section of the shaft and indicate the points of maximum tension and compression.arrow_forwardThe axle of the freight train is subjected to loadings as shown below. The diameter of the axle is 137.5 mm. If it is supported by two journal bearings at C and D, determine the maximum bending stress. Include a FBD, SFD and BMD using either the section or graphical method. Draw a cross-section of the shaft and indicate the points of maximum tension and compression. A B 250 mm 100 kN 1500 mm- Answer 0= +98 MPa 250 mm 100 kNarrow_forwardFor the beam shown at right, determine the following: P= 1800 lb a. Maximum tensile bending stress b. Transverse shear stress at a the junction of the "TEE" (i.e., 2" above the neutral axis). c. Transverse shear stress at the neutral axis - 7.5 ft- - 7.5 ft- (a) d. Draw the stress elements -10 in. representing the state of stress at the junction of the “TEE" and at the neutral axis. | 2 in. 4 in. -N- 1600 10 in. 8 in. 42 in.k- (b)arrow_forward
- What is the max distributed load Wmaxarrow_forwardDetermine the maximum shear stress acting in the fiberglass beam at the section where the internal shears force is maximum. (t1=15 mm, t2=20 mm, h=150 mm, b=50mm)arrow_forward2. If the bending stress at section 2 =20 MPa. What are the bending stresses at sections 1, 3, and 4. 12 mm 12 mm 12 mm 276 mm N.A.- 12 mm 150 mmarrow_forward
- The cross-section of a wooden, built-up beam is shown below. The dimensions are L= 170 mm and w = 30 mm. Determine the magnitude of the moment M that must be applied to the beam to create a compressive stress of σD = 28 MPa at point D. Also calculate the maximum stress developed in the beam. The moment M is applied in the vertical plane about the geometric center of the beam. M = kN.m Omax = MPa W พ L D พ Warrow_forwardA member having the dimensions shown is used to resist an internal bending moment of M kNm. Determine the maximum stress in the member if the moment is applied (a) about the z axis (as shown) (b) about the y axis. Sketch the stress distribution for each case. Take: M= 90 kNm A mm A= 200 mm B= 150 mm B mm Solution: The moment of inertia of the cross-section about z and y axes are I;-4 1 - AB³ 12 (10) m* I BA = (10) m*arrow_forwardIf the angle of the moment M = 170 kN.m on the square section with a side length b = 160 mm in the figure is e = 45 °, which of the following is the highest compressive stress in the section in MPa?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Mechanics of Materials Lecture: Beam Design; Author: UWMC Engineering;https://www.youtube.com/watch?v=-wVs5pvQPm4;License: Standard Youtube License