
Concept explainers
A projectile of mass m moves to the right with a speed νi (Fig. P11.51a). The projectile strikes and sticks to the end of a stationary rod of mass M, length d. pivoted about a frictionless axle perpendicular to the page through O (Fig. PH.51b). We wish to find the fractional change of kinetic energy in the system due to the collision, (a) What is the appropriate analysis model to describe the projectile and the rod? (b) What is the
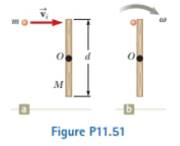
(a)
The appropriate analysis model to describe the projectile and the rod.
Answer to Problem 11.51AP
The appropriate analysis model to describe the projectile and the rod is isolated system (angular momentum).
Explanation of Solution
Given info: The mass of the projectile is
From the conservation of the law of angular momentum the total angular momentum of the system remains constant when the net external torque acting on the system about the given axis is
It is clear from the given explanation and the figure that there is no external force that acts on the rod or the ball and so the angular momentum of the isolated system will remain conserved and so the model for the angular moment of the isolated system will be appropriate model for analysis of projectile and rod.
Conclusion:
Therefore, the appropriate analysis model to describe the projectile and the rod is isolated system (angular momentum).
(b)
The angular momentum of the system before an collision about an axis through
Answer to Problem 11.51AP
The angular momentum of the system before an collision about an axis through
Explanation of Solution
Given info: The mass of the projectile is
The distance from the origin to the ball is,
Here,
The formula to calculate the moment of inertia of the ball about the point
Here,
Substitute
The expression for the initial angular moment of the ball is,
Here,
The relation between the angular speed and the linear speed is,
Substitute
Substitute
Conclusion:
Therefore, the angular momentum of the system before an collision about an axis through
(c)
The momentum of inertia of the system about an axis through
Answer to Problem 11.51AP
The momentum of inertia of the system about an axis through
Explanation of Solution
Given info: The mass of the projectile is
From part (b) the moment of inertia of the ball is
The formula to calculate the moment of inertia of the rod about the point
The moment of inertia of the system when projectile sticks to the rod is,
Here,
Substitute
Conclusion:
Therefore, the momentum of inertia of the system about an axis through
(d)
The angular momentum of the system after collision.
Answer to Problem 11.51AP
The angular momentum of the system after collision is
Explanation of Solution
Given info: The mass of the projectile is
The expression for the final angular moment of the ball is,
Here,
From part (c) momentum of inertia of the system about an axis through
Substitute
Conclusion:
Therefore, the angular momentum of the system after collision is
(e)
The angular speed
Answer to Problem 11.51AP
The angular speed
Explanation of Solution
Given info: The mass of the projectile is
From the law of conservation of angular momentum the expression for the angular momentum is,
Substitute
Conclusion:
Therefore, the angular speed
(f)
The kinetic energy of the system before collision.
Answer to Problem 11.51AP
The kinetic energy of the system before collision is
Explanation of Solution
Given info: The mass of the projectile is
The formula to calculate the kinetic energy of the system is,
Here,
Substitute
Conclusion:
Therefore, the kinetic energy of the system before collision is
(g)
The kinetic energy of the system after collision.
Answer to Problem 11.51AP
The kinetic energy of the system after collision is
Explanation of Solution
Given info: The mass of the projectile is
The expression for the final kinetic energy of the system is,
Here,
From part (c) momentum of inertia of the system about an axis through
And from part (e) the angular speed
Substitute
Conclusion:
Therefore, the kinetic energy of the system after collision is
(h)
The fractional change of kinetic energy due to collision.
Answer to Problem 11.51AP
The fractional change in the kinetic energy of the system is
Explanation of Solution
Given info: The mass of the projectile is
The expression to calculate the change in the kinetic energy of the system is,
Here,
From part (g) kinetic energy of the system after collision is
Substitute
Thus, the change in the kinetic energy is
The formula to calculate the fractional change in the kinetic energy is,
Substitute
Conclusion:
Therefore, the fractional change in the kinetic energy of the system is
Want to see more full solutions like this?
Chapter 11 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- pls help asaparrow_forwardpls help asaparrow_forward2. Max is swimming across a river that is 42.6 m wide. He can swim at 1.6 m/s and heads 20° to the right of the vertical. There is a current pushing him more to the right and it has a speed of 0.30 m/s. Determine the time it takes him to cross the river and find out how far downstream he ends up. Draw the diagram.arrow_forward
 Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill





