
Concept explainers
What is the coordination number of each sphere in (a) a simple cubic cell, (b) a body-centered cubic cell, and (c) a face-centered cubic cell? Assume the spheres are all the same.
(a)
Interpretation:
The co-ordination number of each sphere in simple cubic unit cell, body-centered cubic unit cell and face-centered cubic unit cell have to be identified.
Concept Introduction:
The simplest and basic unit of a crystalline solid is known as unit cell. It is cubic in shape. It is the building block of crystalline solids. The unit cells repeat themselves to build a lattice. Crystalline solids consist of many of such lattices. There are three types of unit cell – simple cubic unit cell, body – centered cubic unit cell and face – centered cubic unit cell.
In packing of the components in a solid, the components are imagined as spheres. A simple cubic unit cell is the simplest form of a cubic unit cell. A cube has eight vertices, twelve edges and six faces. Similarly a cubic unit cell has eight vertices, twelve edges and six faces. If in a cubic unit cell, the components occupy only the eight vertices, then the unit cell is known as simple cubic unit cell. So, each simple cubic unit cell has
In a body – centered cubic unit cell is another type of unit cell in which atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further one atom occupies the center of the cube. Thus the number of atoms per unit cell in BCC unit cell is,
In a face – centered cubic unit cell the atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further all the six faces of a cubic unit cell are occupied with one atom per face. Thus the number of atoms per unit cell in FCC unit cell is,
Co-ordination number of an atom or sphere is termed as the number of spheres it touches in the unit cell.
Answer to Problem 11.37QP
Co-ordination number of simple cubic unit cell is six.
Explanation of Solution
In simple cubic unit cell each sphere at the corner of the cubic unit cell is shared by eight other spheres. Each sphere is surrounded by six spheres.
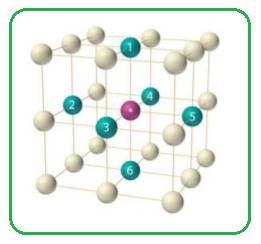
Figure 1
Thus the co-ordination number of simple cubic unit cell is six.
(b)
Interpretation:
The co-ordination number of each sphere in simple cubic unit cell, body-centered cubic unit cell and face-centered cubic unit cell have to be identified.
Concept Introduction:
The simplest and basic unit of a crystalline solid is known as unit cell. It is cubic in shape. It is the building block of crystalline solids. The unit cells repeat themselves to build a lattice. Crystalline solids consist of many of such lattices. There are three types of unit cell – simple cubic unit cell, body – centered cubic unit cell and face – centered cubic unit cell.
In packing of the components in a solid, the components are imagined as spheres. A simple cubic unit cell is the simplest form of a cubic unit cell. A cube has eight vertices, twelve edges and six faces. Similarly a cubic unit cell has eight vertices, twelve edges and six faces. If in a cubic unit cell, the components occupy only the eight vertices, then the unit cell is known as simple cubic unit cell. So, each simple cubic unit cell has
In a body – centered cubic unit cell is another type of unit cell in which atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further one atom occupies the center of the cube. Thus the number of atoms per unit cell in BCC unit cell is,
In a face – centered cubic unit cell the atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further all the six faces of a cubic unit cell are occupied with one atom per face. Thus the number of atoms per unit cell in FCC unit cell is,
Co-ordination number of an atom or sphere is termed as the number of spheres it touches in the unit cell.
Answer to Problem 11.37QP
Co-ordination number of Body-centered cubic unit cell is eight.
Explanation of Solution
There are two spheres per BCC unit cell. Each sphere touches eight other spheres.
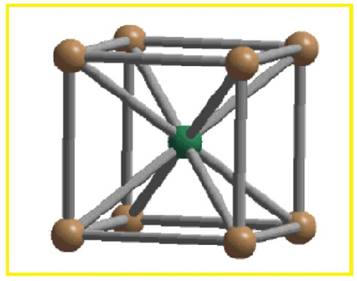
Figure 2
Thus the co-ordination number of body-centered cubic unit cell is eight.
(c)
Interpretation:
The co-ordination number of each sphere in simple cubic unit cell, body-centered cubic unit cell and face-centered cubic unit cell have to be identified.
Concept Introduction:
The simplest and basic unit of a crystalline solid is known as unit cell. It is cubic in shape. It is the building block of crystalline solids. The unit cells repeat themselves to build a lattice. Crystalline solids consist of many of such lattices. There are three types of unit cell – simple cubic unit cell, body – centered cubic unit cell and face – centered cubic unit cell.
In packing of the components in a solid, the components are imagined as spheres. A simple cubic unit cell is the simplest form of a cubic unit cell. A cube has eight vertices, twelve edges and six faces. Similarly a cubic unit cell has eight vertices, twelve edges and six faces. If in a cubic unit cell, the components occupy only the eight vertices, then the unit cell is known as simple cubic unit cell. So, each simple cubic unit cell has
In a body – centered cubic unit cell is another type of unit cell in which atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further one atom occupies the center of the cube. Thus the number of atoms per unit cell in BCC unit cell is,
In a face – centered cubic unit cell the atoms are arranged in all the eight vertices of the unit cell with one atom per vertex. Further all the six faces of a cubic unit cell are occupied with one atom per face. Thus the number of atoms per unit cell in FCC unit cell is,
Co-ordination number of an atom or sphere is termed as the number of spheres it touches in the unit cell.
Answer to Problem 11.37QP
Co-ordination number of Face-centered cubic unit cell is twelve.
Explanation of Solution
There are four spheres per FCC unit cell. Each sphere is in contact with twelve spheres.
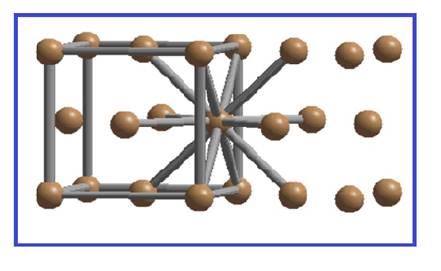
Figure 3
Thus the co-ordination number of simple cubic unit cell is twelve.
Want to see more full solutions like this?
Chapter 11 Solutions
Chemistry
- QUESTION: Fill out the answers to the empty green boxes attached in the image. *Ensure you all incorporate all 27 values (per column)*arrow_forwardYou need to make a buffer by dissolving benzoic acid and sodium benzoate in water. What is the mass of benzoic acid that you would weigh out, in mg, to create 50 mL of a buffer at pH = 4.7 that will change pH no more than 0.10 units with the addition of 0.001 moles of acid or base? Enter just the answer without the units (mg) - just the number will do!arrow_forwardDraw the formula for 3-isopropylcyclopentane-1-carbonyl chloride.arrow_forward
- QUESTION: Fill out the answers to the empty green boxes attached in the image. *Ensure you all incorporate all 27 values (per column)*arrow_forwardComplete the following reactions- hand written pleasearrow_forwardGive the organic product: O A O B Ос ○ D -NH–CH3 + CH3 CH3 NEN C ? A CH3 CH3 NH- CH3 B CH3 CH3 N=N- C CH3 CH3 N=NNH CH3 D CH3 N=N CH3 NHCH3 LNH CHOarrow_forward
- Finish the reaction- hand written pleasearrow_forwardGive the organic products: (benzyne) Br ? CH3 + K* :NH, liq NH3 HINT: Two products are formed. Each is a substituted aniline; they are isomers of each other. NH2 II I H₂N. CH3 CH3 III Select one: ○ A. I and II ○ B. I and III O C. I and IV O D. II and III O E. III and IV H₂N CH3 IV CH₂-NH2arrow_forwardPredict the major products of this organic reaction: HBr (1 equiv) cold ? Some important notes: • Draw the major product, or products, of this reaction in the drawing area below. • You can draw the products in any arrangement you like. • Pay careful attention to the reaction conditions, and only include the major products. • Be sure to use wedge and dash bonds when necessary, for example to distinguish between major products that are enantiomers. • Note that there is only 1 equivalent of HBr reactant, so you need not consider the case of multiple additions. Erase something Explanation Check 2025 McGraw Hill LLC. All Rights Reserved. Terarrow_forward
- Q14. Fill this chart: (please refer to ppt notes/browser to answer these questions) What alcohol is also called wood alcohol? What is the common name of ethanol? Draw the structure of phenol and thiophene? Are bigger chain alcohol like heptanol and octanol are soluble or insoluble in water and explain it ? Are ethers soluble or insoluble in water? What suffix and prefix are used for alcohol while naming alcohol and ether? What the process called when we add water to any alkene to make alcohol? Q16. Draw the diagram of following aromatic compound (practice from previous module) Aniline Phenol Benzoic acid Methyl benzoate Q17. a. Write the oxidation reactions for the 2 propanol. b. Write the oxidation reaction of the ethanol.arrow_forwardQuestion 11 of 18 (1 point) Question Attempt: 3 of How many signals do you expect in the 'H NMR spectrum for this molecule? Br Br Write the answer below. Also, in each of the drawing areas below is a copy of the molecule, with Hs shown. In each copy, one of the H atoms is colored red. Highlight in red all other H atoms that would contribute to the same signal as the H already highlighted red. Note for advanced students: In this question, any multiplet is counted as one signal. Number of signals in the 'H NMR spectrum. 1 For the molecule in the top drawing area, highlight in red any other H atoms that will contribute to the same signal as the H atom already highlighted red. If no other H atoms will contribute, check the box at right. No additional Hs to color in top molecule Check For the molecule in the bottom drawing area, highlight in red any other H atoms that will contribute to the same signal as the H atom already highlighted red. If no other H atoms will contribute, check the box…arrow_forwardOrganic Chemistry Esterification reactions 1. Write the steps to prepare ester. 2. Write complete reaction of ethanol and acetic acid to make ester. 3. What does ester smell like? What are the uses of ester. 4. What the role of sulfuric acid in the esterification reactionarrow_forward
 Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning
Chemistry: Principles and PracticeChemistryISBN:9780534420123Author:Daniel L. Reger, Scott R. Goode, David W. Ball, Edward MercerPublisher:Cengage Learning Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning
Principles of Modern ChemistryChemistryISBN:9781305079113Author:David W. Oxtoby, H. Pat Gillis, Laurie J. ButlerPublisher:Cengage Learning Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning,
Physical ChemistryChemistryISBN:9781133958437Author:Ball, David W. (david Warren), BAER, TomasPublisher:Wadsworth Cengage Learning, ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning
Chemistry: An Atoms First ApproachChemistryISBN:9781305079243Author:Steven S. Zumdahl, Susan A. ZumdahlPublisher:Cengage Learning





